4.2 Représentation polaire et transformations
Définition
Tout point du plan, et donc aussi
tout nombre complexe, peut être représenté
sous forme polaire.
Soit \(z=x+i y\in\mathbb{C}\).
La forme polaire de \(z\) est la donnée
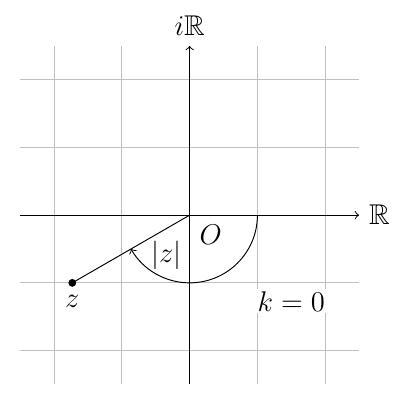
- du module \(r=|z|\), qui représente la distance de \(z\) à \(O\),
- de l'angle \(\varphi\) entre l'axe réel et le rayon-vecteur pointant vers
\(z\), appelé argument de \(z\)
noté \(\arg(z)\).
On écrit alors \(z=[r,\varphi]\).
Bien-sûr, l'argument n'est pas unique, mais déterminé
à un multiple de \(2\pi\) près.
On appelle argument principal de
\(z\) l'unique argument tel que
\[\arg(z) \in \:]\,{-\pi}\,,\,\pi\,]\,.\]
Sur l'animation ci-dessous, on a représenté l'argument principal
\(\theta=\arg(z)\):
Ce dont il faudra se souvenir lorsqu'on voudra résoudre des équations avec des
nombres complexes:
Soit \(z=[r,\varphi]\) et \(z' = [r',\varphi']\). Alors
\[
z=z'
\quad\Leftrightarrow\quad
r=r' \text{ et } \varphi = \varphi' + k2\pi, k\in \mathbb{Z}.
\]
Remarquons que si \(z=[r,\varphi]\in\mathbb{C}\), alors
- \(\bar{z}=[r,-\varphi]\), et
- pour \(\lambda\gt 0\), on a \(\lambda z=\lambda[r,\varphi]
=[\lambda r,\varphi]\).
- si \(z\neq 0\),
\[
\frac{1}{z}
=\frac{\overline{z}}{z\overline{z}}
=\frac{\overline{z}}{|z|^2}
=\frac{1}{r^2}\overline{z}
=\frac{1}{r^2}[r,-\varphi]
=\bigl[\tfrac1r,-\varphi\bigr]\,.
\]
Passage d'une forme à l'autre
Si on a un complexe donné sous forme polaire,
\(z=[r,\varphi]\), alors
\(\mathrm{Re} (z) = r\cos\varphi\) et \(\mathrm{Im} (z) = r\sin\varphi\) et donc
sa forme cartésienne est
\[z=r(\cos\varphi + i\sin\varphi)\,.\]
Inversément, si un complexe \(z\) est donné sous forme cartésienne,
\(z=a+ib\in\mathbb{C}\), alors on peut le mettre sous forme polaire, \(z=[r,\varphi]\)
en prenant \(r=|z|=\sqrt{a^2+b^2}\), et \(\varphi\) un angle quelconque
satisfaisant
\[
\cos\varphi=\frac{a}{\sqrt{a^2+b^2}}
\qquad\text{ et }
\sin\varphi=\frac{b}{\sqrt{a^2+b^2}}\,.
\]
Remarquons que la recherche d'un argument nécessite que les deux
conditions (sur \(\cos\varphi\) et \(\sin\varphi\)) soient satisfaites
simultanément. Si on n'en considère qu'une seule, on pourra trouver un argument
en localisant bien \(z\) pour en extraire l'information nécessaire pour
conclure.
Exemple:
Trouvons une représentation polaire pour \(z=-\sqrt{3}-i\).
Pour commencer, \(r=|z|=\sqrt{3+1}=2\). Ensuite, cherchons un angle
\(\varphi\) tel que
\[
\cos\varphi = -\frac{\sqrt{3}}{2}\,,
\]
Toutes les solutions de cette équation sont
\[
\varphi = \frac{5\pi}{6} + k2\pi\,,\;k\in\mathbb{Z}
\qquad \text{ ou } \qquad
\varphi
= \frac{-5\pi}{6} + k2\pi\,,\;k\in\mathbb{Z}\,.
\]
Comme notre complexe \(z\) appartient au quadrant \(III\), on ne peut garder que
les angles \(\varphi\) du deuxième ensemble de solutions, puisque tous satisfont
\(\sin(\varphi)=-\frac12\).
Par exemple, avec \(k=0\), \(\varphi=-\frac{5\pi}{6}\), et donc
\[
z=\bigl[2,\tfrac{-5\pi}{6}\bigr]\,.
\]
(On pourrait aussi prendre \(k=1\) et obtenir \(z=[2,\frac{7\pi}{6}]\), etc.)
Produit complexe en représentation polaire
Multiplions deux complexes
\(z_1=[r_1,\varphi_1]\) et \(z_2=[r_2,\varphi_2]\).
Puisque
\[\begin{aligned}
z_1&=r_1(\cos\varphi_1+i\sin\varphi_1)\,,\\
z_2&=r_2(\cos\varphi_2+i\sin\varphi_2)\,,
\end{aligned}\]
nous avons
\[\begin{aligned}
z_1z_2 &= r_1r_2(\cos\varphi_1+i\sin\varphi_1)(\cos\varphi_2+i\sin\varphi_2) \\
&= r_1r_2 \bigl((\cos\varphi_1\cos\varphi_2-\sin\varphi_1\sin\varphi_2)
+ i(\cos\varphi_1\sin\varphi_2+\sin\varphi_1\cos\varphi_2) \bigr) \\
&= r_1r_2 \bigl(\cos(\varphi_1+\varphi_2)
+i \sin(\varphi_1+\varphi_2) \bigr)\,.
\end{aligned}\]
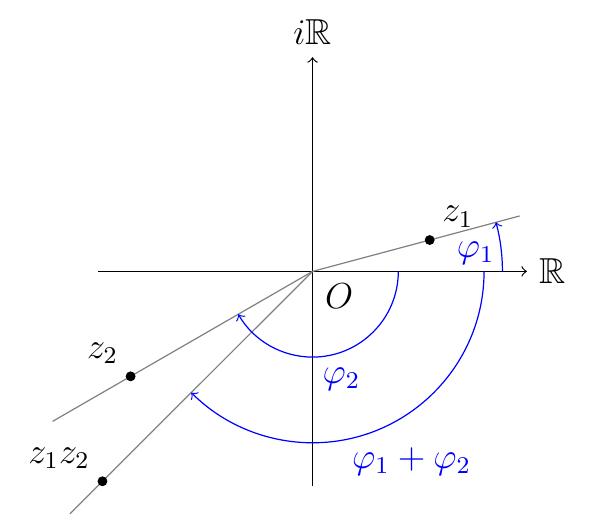
On a donc montré que
\[
z_1z_2
=[r_1,\varphi_1]\cdot [r_2,\varphi_2]
=\bigl[r_1r_2,\varphi_1+\varphi_2\bigr]\,.
\]
Donc multiplier, en représentation polaire, revient
à multiplier les modules et additionner les arguments.
On en conclut que lorsqu'on
divise deux nombres complexes, on divise les modules et on soustrait
les argument. En effet,
\[\frac{z_1}{z_2}=z_1 \cdot\frac{1}{z_2}
= [r_1,\varphi_1] \cdot \left[\tfrac{1}{r_2},-\varphi_2\right]
= \left[\frac{r_1}{r_2},\varphi_1-\varphi_2\right]\,.
\]
Exemple:
Pour \(z_1=(\sqrt{2},\frac{\pi}{12})\) et \(z_2=(\sqrt{6},-\frac{5\pi}{6})\),
\[\begin{aligned}
|z_1z_2| &= \sqrt{2} \sqrt{6} = 2\sqrt{3} \\
\arg(z_1z_2) &= \frac{\pi}{12}-\frac{5\pi}{6} = -\frac{9\pi}{12}= -\frac{3\pi}{4}
\end{aligned}\]
Donc \[z_1z_2 = \textstyle\bigl(2\sqrt{3},-\frac{3\pi}{4}\bigr)\,.\]
On peut utiliser les propriétés de l'argument pour calculer des
angles dans le plan.
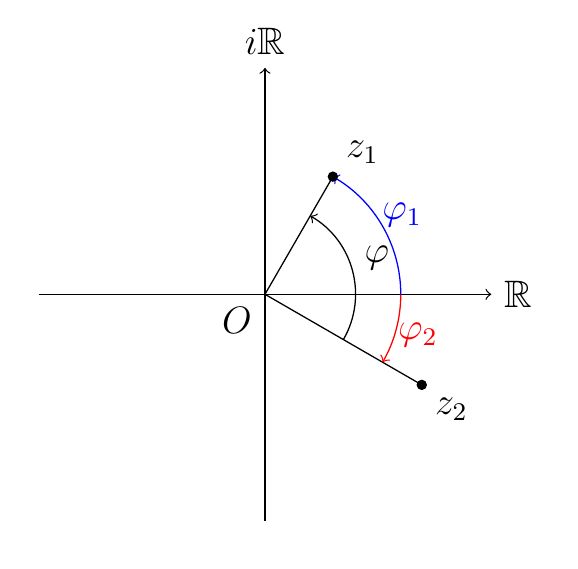
En effet, pour deux complexes
\(z_1=[r_1,\varphi_1]\) et \(z_2=[r_2,\varphi_2]\),
\[
\varphi
=\widehat{z_2Oz_1}
=\varphi_1-\varphi_2
=\arg(z_1)-\arg(z_2)
=\arg\left(\frac{z_1}{z_2}\right)\,.\]
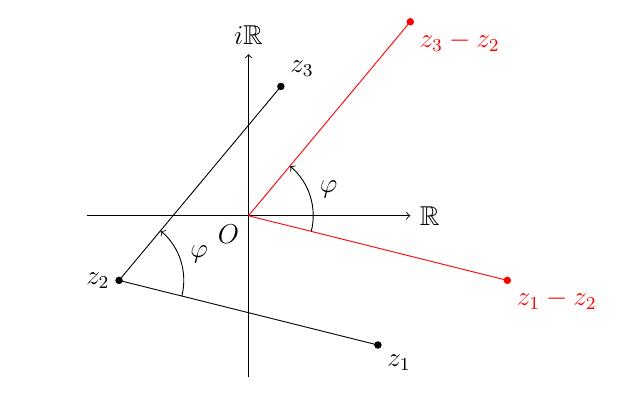
Plus généralement, l'angle formé par trois complexes
\(z_1,z_2,z_3\) (dans cet ordre):
\[
\varphi
=\widehat{z_1z_2z_3}
=\widehat{(z_1-z_2)O(z_3-z_2)}
=\arg\left(\frac{z_3-z_2}{z_1-z_2}\right)\,.
\]
La formule de Moivre
Appliquons la formule du produit dans le cas où
\(z_1=z_2=z=[r,\varphi]\):
\[ z^2=z\cdot z=[r,\varphi]\cdot[r,\varphi]=[r^2,2\varphi]\,.
\]
Cette formule est un cas particulier de la
formule de Moivre:
Théorème:
Soit \(z=[r,\varphi]\). Alors pour tout entier \(n\geqslant 2\),
\[
z^n
=[r^n,n\varphi]
=r^n\bigl(\cos(n\varphi)+i\sin(n\varphi) \bigr)
\,.
\]
Preuve:
On a vu juste au-dessus que la formule
est vraie pour \(n=2\).
Si on suppose que
la formule est vraie pour \(n\), \(z^n=[r^n,n\varphi]\), alors
\[
z^{n+1}
= z^n\cdot z
= [r^n,n\varphi] \cdot [r,\varphi]
= [r^n r,n\varphi+\varphi]
= [r^{n+1},(n+1)\varphi]\,,
\]
et donc elle est vraie aussi pour \(n+1\).
Géométrie et transformations dans le plan complexe
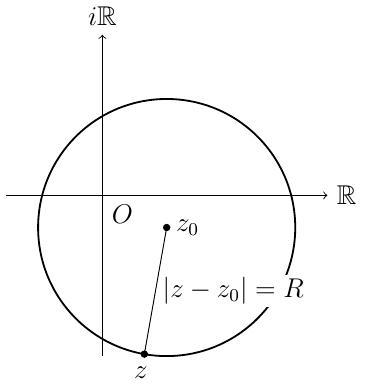
Soient \(z\) et \(z_0\) deux points du plan complexe.
La distance de \(z\) à \(z_0\) est
\[\text{dist}(z,z_0) = |z-z_0|\,. \]
Equation d'un cercle centré à l'origine et de rayon \(R\):
\[|z|^2 = z\bar{z} = R^2\,.\]
Equation d'un cercle centré en \(z_0\) et de rayon \(R\):
\[|z-z_0|^2 = R^2\,.\]
Considérons maintenant un complexe \(z\), et interprétons géométriquement
l'effet qu'ont sur \(z\)
les opérations élémentaires d'addition et de multiplication.
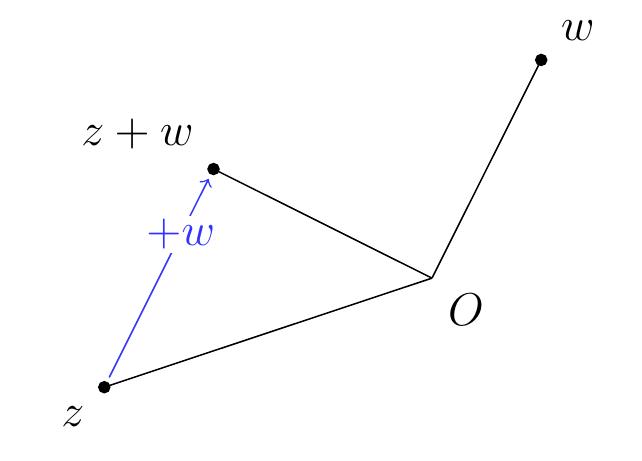
Translation
Si \(w\in \mathbb{C}\), alors l'opération
\[ z\mapsto z+w
\]
correspond à faire une translation de \(z\).
On visualise cette opération comme la règle du parallélogramme pour l'addition
en géométrie vectorielle:
Rotation
Dans \(\mathbb{C}\), la multiplication par un nombre complexe \(w\) de module \(1\),
\[
z\mapsto \omega z\,,
\]
correspond à une rotation d'angle
\(\arg(\omega)\) autour de l'origine.
En effet, si \(z=[r,\varphi]\) et \(\omega=[1,\theta]\), alors
\[\begin{aligned}
\omega z
&=[1,\theta] \cdot [r,\varphi] \\
&=[r,\varphi+\theta]
\end{aligned}\]
On pourra donc écrire \(\omega z=\text{rot}_\theta(z)\).
Sur l'animation ci-dessous,
\(\omega\) est sur le cercle de rayon \(1\) centré à l'origine:
Homothétie
La multiplication de \(z\) par un réel \(\lambda\in\mathbb{R}\),
\[
z\mapsto \lambda z
\]
correspond à une homothétie.
On appelle \(\lambda\) le rapport de l'homothétie.
- Si \(\lambda\gt 0\),
alors \(\arg(\lambda z)=\arg(z)\), et
\(\lambda z\) représente un agrandissement (si \(\lambda
\gt 1\))
ou une réduction (si \(0\lt \lambda \lt 1\)) de \(z\), de facteur
\(\lambda\).
- Si \(\lambda\lt 0\),
alors \(\arg(\lambda z)=\arg(z)+\pi\), et
\(\lambda z\) représente une rotation de \(+\pi\), composée avec
un agrandissement ou une réduction de facteur \(|\lambda|\).
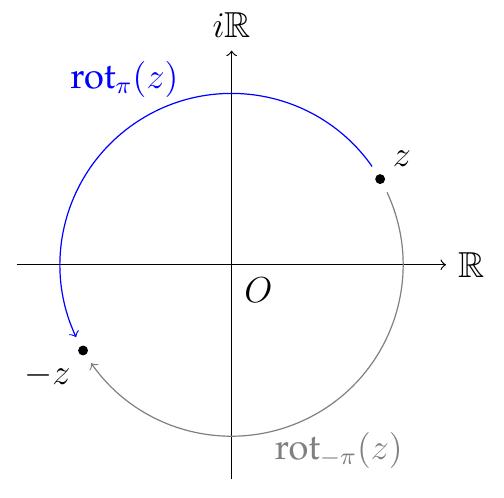
En particulier, la multiplication de \(z\) par \(\lambda=-1=[1,\pi]\)
donne \(-z\), le symétrique de \(z\) par rapport à l'origine \(O\),
et peut aussi se voir comme une rotation d'un angle \(\pi\) (ou \(-\pi\)):
\[(-1)z =-z = \text{rot}_\pi(z)\,.\]
Similitude
La multiplication de \(z\) par un complexe \(\omega\) quelconque,
\[
z\mapsto \omega z
\]
correspond à une similitude, c'est-à-dire une rotation composée avec une
homothétie. En effet, en travaillant en représentation polaire,
\(\omega=[\rho,\theta]=\rho[1,\theta]\),
on peut écrire \(\omega z=\rho([1,\theta]z)\). Comme
\([1,\theta] z =\text{rot}_\theta(z)\),
\(z\mapsto \omega z\) est la composition de deux transformations,
\[
z
\mapsto
\text{rot}_\theta(z)
\mapsto
\rho(\text{rot}_\theta(z))=\omega z\,,
\]
la première étape étant une rotation d'angle \(\theta=\arg(\omega)\), la
deuxième une homothétie de rapport \(\rho=|\omega|\):
Une remarque à propos de l'équation d'une droite dans \(\mathbb{C}\):
Considérons l'équation générale d'une droite dans le plan \(\mathbb{R}^2\):
\[
ax+by=c\,,
\]
avec \(a,b,c\in\mathbb{R}\).
Si maintenant on la reformule en terme de \(z=x+i y\),
\[a\mathrm{Re} (z) + b\mathrm{Im} (z) = c \,.\]
On peut récrire cette dernière
\[
a\frac{z+\bar{z}}{2} + b\frac{z-\bar{z}}{2i} = c \,,
\]
ou encore
\[
\frac{(a-ib)z + (a+ib) \bar{z}}{2}=c\,.
\]
En définissant \(u=a+ib\), cette dernière se lit comme
\[
\frac{\bar{u}z + u\bar{z}}{2}=c\,.
\]
Puisque \(u\bar{z}=\bar{\bar{u}z}\), le membre de gauche
\[
\frac{\bar{u}z + u\bar{z}}{2}=\mathrm{Re} (\bar{u}z)\,.
\]
Donc l'équation de la droite \(ax+by=c\) s'écrit, dans les complexes,
comme
\[
\mathrm{Re} (\bar{u}z) = c\,.
\]
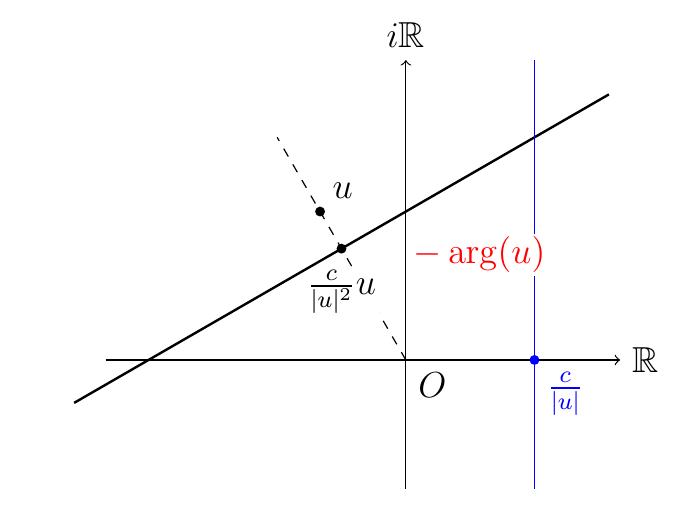
Interprétons géométriquement cette formulation:
\(u=a+ib\) est clairement le nombre complexe directeur de la normale à la
droite. En effectuant une rotation d'angle \(-\arg(u)=\arg(\bar{u})\) de tous
les points \(z\) de la droite en les multipliant par \(\bar{u}/|u|\), on obtient
effectivement une droite verticale.
Racines \(n\)-èmes de nombres complexes
Un complexe \(\omega\) est appelé
racine \(n\)-ème de l'unité si
\[
\omega^n=1\,.
\]
On résout cette équation en posant \(\omega = [r,\varphi]\) et
\(1=[1,0]\). Par la formule de Moivre,
\[
\omega^n=[r^n,n\varphi]\,,
\]
et donc l'équation devient
\[
[r^n,n\varphi]=[1,0]\,.
\]
Or on a vu plus haut que
l'égalité de deux nombres complexes sous forme polaire implique
- Modules égaux : \(r^n=1\) \[\Rightarrow r=1 \text{ (car \(r \in\mathbb{R}_+\))}\]
- Arguments égaux à \(k2\pi\) près : \(n\varphi = 0+k2\pi\), \(k\in\mathbb{Z}\),
\[\Rightarrow \varphi = k\,\frac{2\pi}{n} \qquad k\in\mathbb{Z}\,.\]
Il y a donc \(n\) racines distinctes de \(1\):
\[S=\Bigl\{[1,k\,\textstyle\frac{2\pi}{n}] \,\Big|\, k=0,\ldots,n-1 \Bigr\}\,.\]
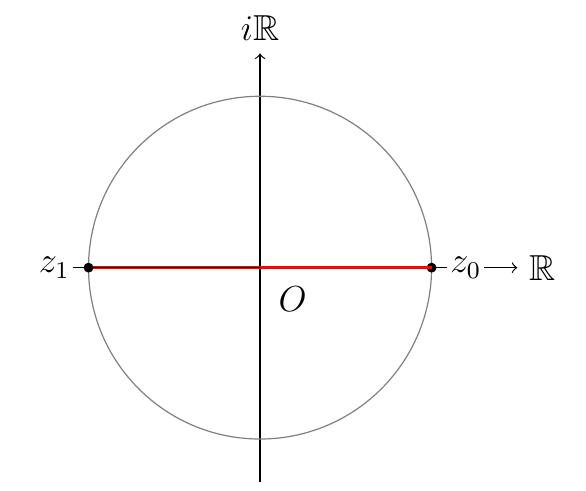
- Pour \(n=2\),
\[S=\Bigl\{[1,k\,\pi] \,\Big|\, k=0,1 \Bigr\}\,.\]
-
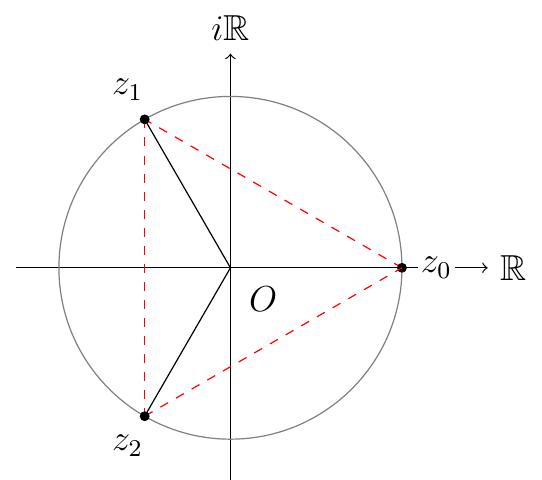
Pour \(n=3\),
\[S=\Bigl\{[1,k\,\textstyle\frac{2\pi}{3}] \,\Big|\, k=0,1,2 \Bigr\}\,.\]
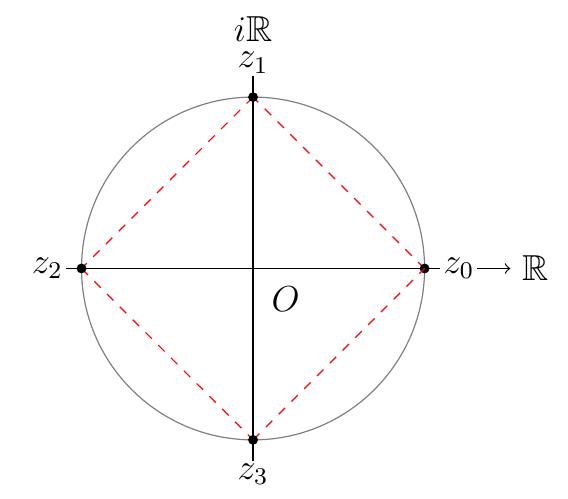
- Pour \(n=4\),
\[S=\Bigl\{[1,k\,\textstyle\frac{\pi}{2}] \,\Big|\, k=0,\ldots,3 \Bigr\}\,.\]
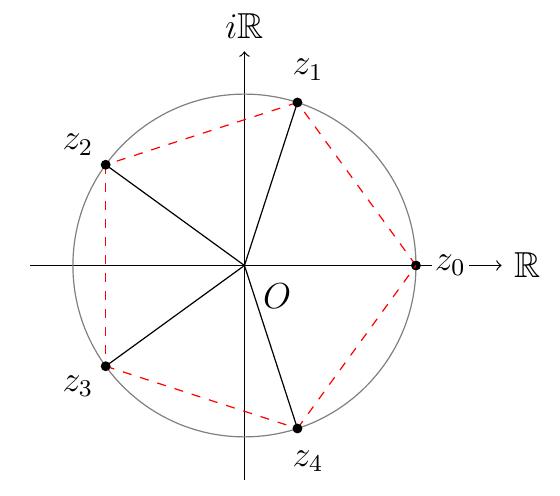
- Pour \(n=5\),
\[S=\Bigl\{(1,k\,\textstyle\frac{2\pi}{5}) \,\Big|\, k=0,\ldots,4 \Bigr\}\,.\]
On peut appliquer la même méthode pour calculer la racine \(n\)-ème d'un
complexe quelconque.
De manière générale, les racines \(n^{\text{e}}\) d'un complexe sont localisées
sur les
sommets d'un polygône régulier à \(n\) côtés inscrit dans un cercle.
Exemple:
Cherchons les racines cubiques de \(8i\), c'est-à-dire les \(\omega\in \mathbb{C}\) tels
que
\[
\omega^3=8i\,.
\]
On pose \(\omega=[r,\varphi]\), et on met \(8i\) sous forme polaire:
\(i=[8,\frac{\pi}{2}]\). En utilisant la formule de Moivre, l'équation devient
\[ [r^3,3\varphi]=[8,\tfrac{\pi}{2}]\,,
\]
qui implique \(r^3=8\), c'est-à-dire \(r=2\),
et
\[
3\varphi=\frac{\pi}{2}+2k\pi\,,\qquad k\in \mathbb{Z}\,,
\]
qui donne \(\varphi=\frac{\pi}{6}+k\frac{2\pi}{3}\), \(k\in \mathbb{Z}\).
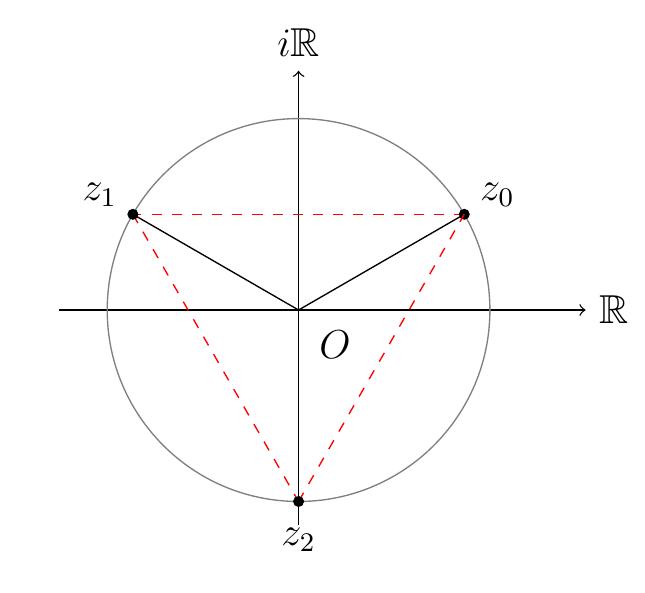
On a donc trois solutions distinctes, en prenant \(k=0,1,2\):
\[
z_0=[2,\tfrac{\pi}{6}]\,,\qquad
z_1=[2,\tfrac{5\pi}{6}]\,,\qquad
z_2=[2,\tfrac{3\pi}{2}]\,.
\]
Ces racines sont aux sommets d'un triangle équilatéral, situés sur un cercle de
rayon \(r=2\) centré à l'origine:
Une remarque sur la forme exponentielle
Pour \(z=[r,\varphi]\),
on définit la forme exponentielle \(z=re^{i\varphi}\).
Les règles de calcul des exponentielles réelles s'appliquent.
En particulier si \(z_1=r_1e^{i\varphi_1}\) et \(z_2=r_2e^{i\varphi_2}\), alors
\[z_1z_2 = r_1r_2 e^{i(\varphi_1 + \varphi_2)}.\]
Cette forme a donc l'avantage de faciliter les calculs sous forme polaire.
Remarque:
- Il est possible de définir une fonction exponentielle complexe \(z\mapsto
e^z\) pour tout \(z\in\mathbb{C}\). Avec cette fonction on peut démontrer l'égalité
\[re^{i\varphi} = r(\cos(\varphi) + i \sin(\varphi)).\] Ceci sort cependant du
cadre du cours, et nous allons admettre l'égalité
\[re^{i\varphi}=[r,\varphi]\]
comme convention et nous pouvons l'utiliser dans les calculs.
- pour
\(z=re^{i\varphi}\),
\(\bar{z} = [r,-\varphi] =re^{-i\varphi}\).
- En particulier, si on pose \(z=e^{i\varphi}=\cos(\varphi)+i\sin(\varphi)\), on a formellement que
\[\cos(\varphi) = \mathrm{Re} (z) = \frac{z+\bar{z}}{2}=\frac{e^{i\varphi}+e^{-i\varphi}}{2}=\cosh(i\varphi)\]
et
\[\sin(\varphi) = \mathrm{Im} (z) = \frac{z+\bar{z}}{2i}=\frac{e^{i\varphi}-e^{-i\varphi}}{2i}=\frac{1}{i}\sinh(i\varphi).\]
On constate que dans le plan complexe, les fonctions trigonométriques et hyperboliques sont les mêmes !
Rappel : pour \(x\in\mathbb{R}\)
\[
\cosh(x) = \frac{e^x + e^{-x}}{2}\,,\qquad
\sinh(x) = \frac{e^x-e^{-x}}{2}.
\]