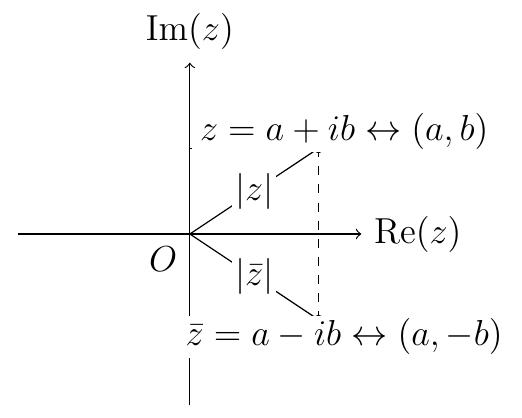4.1 Forme cartésienne
Définition
Nous avons vu, dans la section sur les équations du deuxième degré,
que l'équation \(x^2+1=0\) ne possède pas de solutions puisque le discriminant
de \(x^2+1\) est \(\Delta=-4\). En d'autres termes:
le réel \(-1\) n'a pas de racines carrées, puisqu'il n'existe aucun réel
\(x\) tel que \(x^2=-1\).
Les nombres complexes fournissent
une extension du corps des réels \(\mathbb{R}\) permettant de
résoudre ce type d'équation. Pour cela,
- nous introduisons un
nombre
\(i\) (nombre imaginaire
) tel
que
\[i^2=-1 \]
- nous imposons que tout calcul se fait selon les règles établies sur les
réels.
Remarque: Tout comme \(i^2=-1\), \((-i)^2 = (-1)^2i^2 = i^2 = -1\): \(i\) et
\(-i\) sont les racines de \(-1\).
Pour l'équation en \(x^2=-1\),
l'ensemble solution est \(S=\{-i,i\}\). On obtient ainsi la factorisation
\[x^2+1 = (x+i)(x-i)\,.\]
En effet, \((x+i)(x-i) = x^2-ix+ix-i^2=x^2+1\).
Exemple: Résoudre l'équation en \(x\): \(x^2+x+1=0\). Le discriminant vaut
\(\Delta = 1^2-4 = -3 = (-1)\cdot 3\) et l'ensemble solution est
\[
S=\left\{\frac{-1-i\sqrt{3}}{2},\frac{-1+i\sqrt{3}}{2} \right\}\,.
\]
Nous allons donc devoir manipuler des nombres de la forme
\[z = a + ib, \quad a,b\in\mathbb{R}\,.\]
L'ensemble
\[\mathbb{C} = \{ z = a + ib \,|\, a,b\in\mathbb{R}\}\]
est appelé l'ensemble des nombres complexes.
Soit \(z=a+ib \in\mathbb{C}\), \(a,b\in\mathbb{R}\).
- L'écriture \(z=a+ib\) est appelé forme cartésienne ou forme algébrique.
- \(a\) est la partie réelle de \(z\), que l'on note
\[\mathrm{Re} (z)=a\,.\]
- \(b\) est la partie imaginaire de \(z\), que l'on note
\[\mathrm{Im} (z) = b\,.\]
Ainsi, \(z=\mathrm{Re} (z)+i\mathrm{Im} (z)\) pour tout \(z\in\mathbb{C}\).
Remarque:
\(i\mathbb{R} = \{ ib \,|\, b\in\mathbb{R}\}\) est l'ensemble des nombres imaginaires.
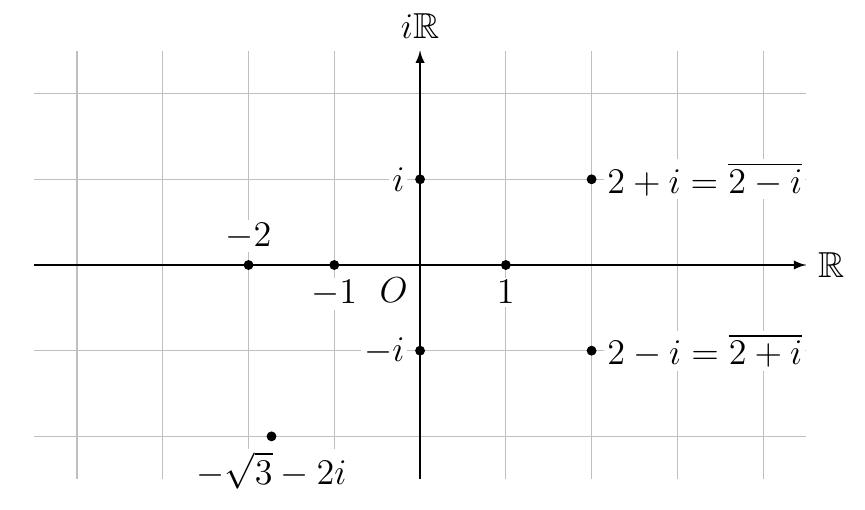
Identification entre \(\mathbb{C}\) et \(\mathbb{R}^2\)
Tout nombre complexe \(z=a+ib\) peut être associé au point
de coordonnées \((a,b)\) dans le plan \(\mathbb{R}^2\), et réciproquement,
à tout point \((a,b)\in \mathbb{R}^ 2\), on associe l'unique nombre complexe \(z=a+ib\).
Lorsque les points du plan \(\mathbb{R}^2\) sont interprétés comme représentant des
nombres complexes, on parle du plan complexe ou
encore du plan de Gauss.
Représentation graphique:
Quelques éléments de géométrie en écriture complexe :
- Si \(z=a+ib\), \(a,b\in\mathbb{R}\), le nombre complexe \(a-ib\) représente
le symétrique de \(z\) par rapport à l'axe réel. On note \(\bar{z}=a-ib\) que
l'on appelle le conjugué de \(z\).
- Equation d'une droite verticale dans le repère \(Oxy\) de \(\mathbb{R}^2\) :
\[
x=a\,.
\]
Equation de la même droite, en écriture complexe:
\[
\mathrm{Re} (z) = a
\quad\Leftrightarrow\quad
z+\bar{z}=2a \in\mathbb{R}\,.
\]
- Equation d'une droite horizontale dans le repère \(Oxy\) de \(\mathbb{R}^2\) :
\[
y=b\,.
\]
Equation de la même droite, en écriture complexe:
\[
\mathrm{Im} (z) = b
\quad\Leftrightarrow\quad
z-\bar{z}=2ib\in i\mathbb{R}\,.
\]
Opérations sur les nombres complexes
Soient \(z=a+ib,z'=a'+ib' \in\mathbb{C}\), \(a,b,a',b'\in\mathbb{R}\).
- Egalité
\[z=z' \Longleftrightarrow \begin{cases}
\mathrm{Re} (z)=\mathrm{Re} (z') \\
\mathrm{Im} (z)=\mathrm{Im} (z')
\end{cases}
\Longleftrightarrow a=a' \text{ et } b=b'\,.\]
- Addition \(+\)
\[z+z' = (a+ib) + (a'+ib') = (a+a') + i(b+b')\]
c'est-à-dire,
\[\mathrm{Re} (z+z') = \mathrm{Re} (z) + \mathrm{Re} (z') \text{ et } \mathrm{Im} (z+z') = \mathrm{Im} (z) + \mathrm{Im} (z')\,.\]
En particulier,
\[\mathrm{Re} (z+z) = 2\mathrm{Re} (z) \text{ et } \mathrm{Im} (z+z) = 2\mathrm{Im} (z)\,.\]
- Multiplication \(\cdot\)
\[\begin{aligned}
zz'
&= (a+ib)(a'+ib') \\
&= aa'+iab'+iba' + i^2bb'\\
&= (aa'-bb') + i(ab'+ba')
\end{aligned}\]
c'est-à-dire
\[\begin{aligned}
\mathrm{Re} (zz') &= \mathrm{Re} (z)\mathrm{Re} (z')-\mathrm{Im} (z)\mathrm{Im} (z') \\
\mathrm{Im} (zz') &= \mathrm{Re} (z)\mathrm{Im} (z')+\mathrm{Im} (z)\mathrm{Re} (z')\,.
\end{aligned}\]
Remarque:
Observer la similitude avec \(\cos(\alpha+\beta)\) et \(\sin(\alpha+\beta)\).
- \(\lambda z = \lambda a + i\lambda b\), \(\lambda\in\mathbb{R}\) (amplification par un réel)
- \(i z = i a + i^2 b = -b + ia\) (amplification par un imaginaire)
- \(zz=z^2=a^2-b^2 + i2ab\) (carré).
Soit \(z=a+ib \in\mathbb{C}\), \(a,b\in\mathbb{R}\).
Le nombre complexe conjugué de \(z\), noté \(\bar{z}\), est le nombre
\[\bar{z} = a-ib\,.\]
Soient \(z,z'\in\mathbb{C}\).
- \(\mathrm{Re} (z)=\displaystyle\frac{z+\bar{z}}{2}\),
\(\mathrm{Im} (z)=\displaystyle\frac{z-\bar{z}}{2i}\)
- \(\overline{\bar{z}}=z\)
- \(\mathrm{Re} (\bar{z}) = \mathrm{Re} (z)\) et \(\mathrm{Im} (\bar{z}) = -\mathrm{Im} (z)\)
- \(\overline{z+z'}=\overline{z}+\overline{z'}\)
- \(\overline{zz'}=\overline{z}\,\overline{z'}\)
- \(z\bar{z} =\mathrm{Re} ^2(z) + \mathrm{Im} ^2(z)\)
- \(\bar{z} = z \Leftrightarrow \mathrm{Im} (z)=0\Leftrightarrow z\in\mathbb{R}\) et
\(\bar{z} = -z \Leftrightarrow \mathrm{Re} (z)=0 \Leftrightarrow z\in i\mathbb{R}\).
Les preuves se font par vérification directe.
Soit \(z=a+ib \in\mathbb{C}\), \(a,b\in\mathbb{R}\). Le module de \(z\), noté \(|z|\),
est le nombre réel positif ou nul
\[|z| = \sqrt{z\bar{z}} = \sqrt{a^2+b^2}=\sqrt{\mathrm{Re} ^2(z)+\mathrm{Im} ^2(z)}.\]
En particulier on a
\[z\bar{z} = (a+ib)+(a-ib) = a^2 + b^2 =|z|^2 \]
Représentation graphique:
On observe que le module représente la distance entre le point \((a,b)\),
identifé avec le nombre \(z=a+ib\), et l'origine \(O=(0,0)\) identifié avec le
nombre \(z=0\). Le conjugué représente le symétrique de \((a,b)\) par symétrie
d'axe horizontal.
- \(|\mathrm{Re} (z)| \leqslant |z|\), \(|\mathrm{Im} (z)| \leqslant |z|\) \qquad\(\forall\,z\in\mathbb{C}\)
- \(|z| = |\bar{z}|\) \(\forall\,z\in\mathbb{C}\)
- \(\displaystyle \frac{1}{z} =
\frac{\bar{z}}{|z|^2}\) \(\forall\,z\in\mathbb{C}^\ast\)
- \(|z_1z_2| = |z_1|\,|z_2| \qquad \displaystyle \left|\frac{z_1}{z_2}\right| =
\frac{|z_1|}{|z_2|}\; (z_2\neq 0)\) \(\forall\,z_1,z_2\in\mathbb{C}\)
- \(|z_1+z_2| \leqslant |z_1| + |z_2|\) \(\forall\,z_1,z_2\in\mathbb{C}\).
Remarque: \((\mathbb{C},+,\cdot)\) est un corps (cf Chapitre 0). On a effet l'existence
- de l'élément neutre pour l'addition : \(0=0+i0\)
- de l'opposé de \(z=a+ib\), \(a,b\in\mathbb{R}\) pour l'addition : \(-z=-(a+ib) = {}-a-ib\)
- de l'élément neutre pour la multiplication : \(1=1+i0\)
- de l'inverse de \(z=a+ib\neq 0\), \(a,b\in\mathbb{R}\) pour la multiplication : \[\frac{1}{z} = \frac{a-ib}{a^2+b^2}\,.\]
En effet, \[\frac{1}{z} = \frac{\bar{z}}{z\bar{z}} = \frac{a-ib}{\vert z \vert^2} = \frac{a-ib}{a^2 + b^2}.\]
L'existence de l'inverse permet de définir la division dans \(\mathbb{C}\).
Soient \(z_1,z_2\in\mathbb{C}\) avec \(z_2\neq0\). Alors
\[ \frac{z_1}{z_2}=z_1 \frac{1}{z_2} = \frac{1}{z_2} \; z_1\,.\]
Puissances et racines
Soient \(z\in\mathbb{C}\) et \(n\in\mathbb{N}^\ast\). Comme pour les réels, \(z\)
puissance \(n\)
signifie
\[z^n = \underset{n \text{ facteurs}}{\underbrace{z\cdot z \cdot \ldots \cdot z}}\,.\]
De plus, si \(z\neq 0\), nous avons les exposants négatifs ou nul
\[z^0 = 1 \qquad z^{-1} = \frac{1}{z} \qquad z^{-n}=\frac{1}{z^n}\,.\]
Soient \(z\in\mathbb{C}\) et \(n\in\mathbb{N}^\ast\). Un nombre \(w\in\mathbb{C}\) est une
racine \(n^\text{e}\) complexe de \(z\) si \(w\) vérifie \(w^n=z\).
Exemple:
Les racines carrées de \(-1\) sont \(i\) et \(-i\).
Exemple: Les racines cubiques de \(-1\) sont données par \(\omega^3 = -1\). On a
\(\omega=\begin{cases} -1 \\ \text{ou} \\ \frac{1+i\sqrt{3}}{2} \\ \text{ou}\\
\frac{1-i\sqrt{3}}{2}\,. \end{cases}\)
En effet,
\((-1)^3=(\frac{1\pm i\sqrt{3}}{2})^3
= \frac{1}{8} (1 \pm i3\sqrt{3} - 9 \mp i3\sqrt{3}) = -1 \).
On peut le trouver en résolvant l'équation
\(z^3 = -1 \Leftrightarrow z^3+1=(z+1)(z^2-z+1)=0\)\, dont on connait les solutions.
Cas particulier: trouver la racine carrée de \(z=a+ib\) sous forme algébrique.\\
Pour \(z=a+ib\), \(a,b\in\mathbb{R}\), on résout \(\omega^2 = z\) avec \(\omega = \alpha + i \beta\). Nous cherchons donc \(\alpha,\beta\in\mathbb{R}\) tels que
\[ (\alpha+i\beta)^2 = \alpha^2 -\beta^2 + i2\alpha\beta = a+ib \Leftrightarrow \begin{cases} \alpha^2 -\beta^2=a \\ 2\alpha\beta = b\,.\end{cases}\]
Plutôt que la relation \(2\alpha\beta = b\), utilisons le carré du
module
\[\alpha^2 + \beta^2 = |\alpha+i\beta|^2 = \left|\sqrt{a+ib}\right|^2 = \sqrt{|a+ib|^2}
= \sqrt{a^2+b^2}\,.\]
Alors
\[ (\alpha+i\beta)^2 = a+ib
\qquad\Leftrightarrow\qquad
\begin{cases} \alpha^2 -\beta^2=a=\mathrm{Re} (z) \\ \alpha^2 +\beta^2=\sqrt{a^2+b^2}=|z|
\\ \mathrm{sgn}(\alpha\beta) = \mathrm{sgn}(b)= \mathrm{sgn}(\mathrm{Im} (z))\,. \end{cases}\]
Exemple:
Calculer les racines de \(i\). On pose \(\omega=\alpha+ i\beta\) et on résout
\(\omega^2=i\).
On a
\[(\alpha+i\beta)^2 = 0 + i\cdot 1 \Leftrightarrow
\begin{cases}
\alpha^2 -\beta^2=\mathrm{Re} (i)=0 \\
\alpha^2 +\beta^2=|i|=1 \\
\mathrm{sgn}(\alpha\beta) = \mathrm{sgn}(\mathrm{Im} (i))=+1
\end{cases}
\Leftrightarrow
\begin{cases}
\alpha^2=\beta^2=\frac{1}{2} \\
\mathrm{sgn}(\alpha\beta) = +1
\end{cases}
\Leftrightarrow
\omega= \pm \frac{1+i}{\sqrt{2}}\,.
\]