2.5 Équations et inéquations avec valeur absolue
Soit \(x\in\mathbb{R}\). La valeur absolue de \(x\), notée \(|x|\), est le réel positif ou nul \[ |x| = \begin{cases} x& \text{si }x\geqslant 0 \\ -x & \text{si }x \lt 0\,. \end{cases} \]

Exemples:

Lorsque la valeur absolue contient une expression qui dépend d'une variable, on doit étudier le signe de cette expression.

Exemple: \[\begin{aligned} |x^2-1| &= \begin{cases} x^2-1&\text{ si }x^2-1\geqslant 0\,,\\ -(x^2-1)&\text{ si }x^2-1\lt 0\,, \end{cases}\\ &= \begin{cases} x^2-1&\text{ si }x\in ]-\infty,-1]\cup[1,+\infty[\,,\\ -(x^2-1)&\text{ si }x\in ]-1,1[\,. \end{cases} \end{aligned}\]

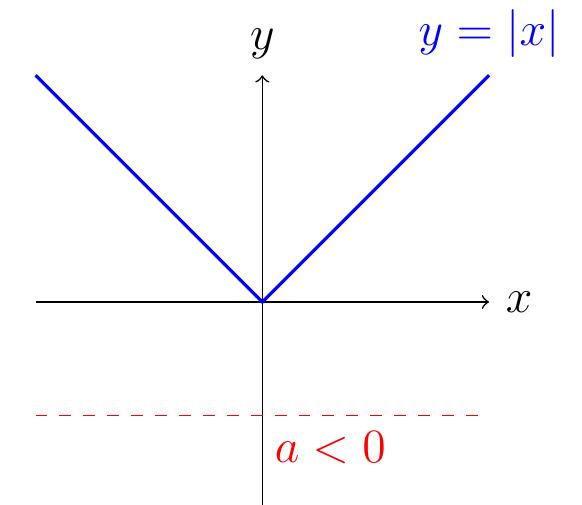
Le graphe de la fonction \(x\mapsto |x|\):

Soient \(x,y\in\mathbb{R}\). Alors
  1. \(|x|\geqslant 0\)
  2. \(|x|= 0 \Leftrightarrow x=0\)
  3. \(|x|^2 = x^2\)
  4. \(|x| = |-x|\)
  5. \(x=\mathrm{sgn}(x)\,|x|\), \(|x|=\mathrm{sgn}(x)\,x\)
  6. \(\vert x \vert = \max(x,-x)\)
  7. \(-|x| \leqslant x \leqslant |x|\)
  8. \(|x+y| \leqslant |x|+|y|\) (inégalité triangulaire)
  9. \(|xy| = |x|\,|y|\).
L'équation \(|x|=a\)

Puisque \(|x|\geqslant 0\) pour tout \(x\in \mathbb{R}\), l'équation \(|x|=a\), \(a\in\mathbb{R}\), ne peut clairement pas avoir de solution si \(a\lt 0\). Ceci s'interprète graphiquement, en voyant que le graphe de \(|x|\) n'intersecte pas une droite horizontale à hauteur \(a\lt 0\):

Théorème: Soit \(a\in\mathbb{R}\). On a l'équivalence \[ |x|=a \qquad\Leftrightarrow \qquad a\geqslant 0 \text{ et } \left\{ \begin{array}{l} x=a \\ \hspace{-3mm}\text{\scriptsize ou} \\ x=-a\,.\end{array} \right.\]

Graphiquement, le graphe de \(|x|\) intersecte une droite horizontale en deux points lorsque celle-ci est à hauteur \(a\gt 0\):

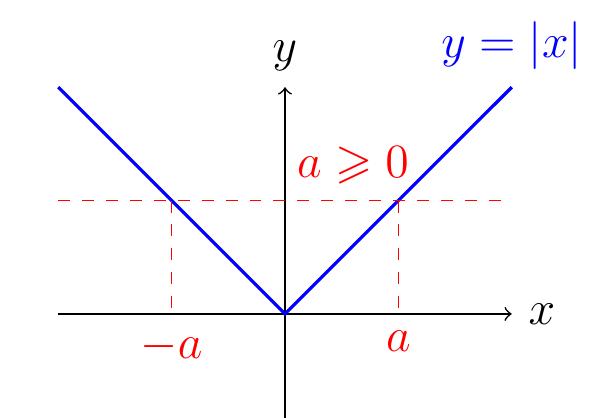
En résumé, l'ensemble solution \(S\) de l'équation \(|x|=a\) est donné par

  1. \(S= \{-a,a\}\) si \(a\geqslant 0\),
  2. \(S= \varnothing\) si \(a\lt 0\).
L'inéquation \(|x|\leqslant a\)

Théorème: Soit \(a\in\mathbb{R}\). On a l'équivalence \[ |x|\leqslant a \qquad\Leftrightarrow \qquad -a\leqslant x\leqslant a \qquad\Leftrightarrow \qquad \left\{ \begin{array}{l} x\leqslant a \\ \hspace{-3mm}\text{\scriptsize et} \\ x\geqslant-a\,.\end{array} \right.\]

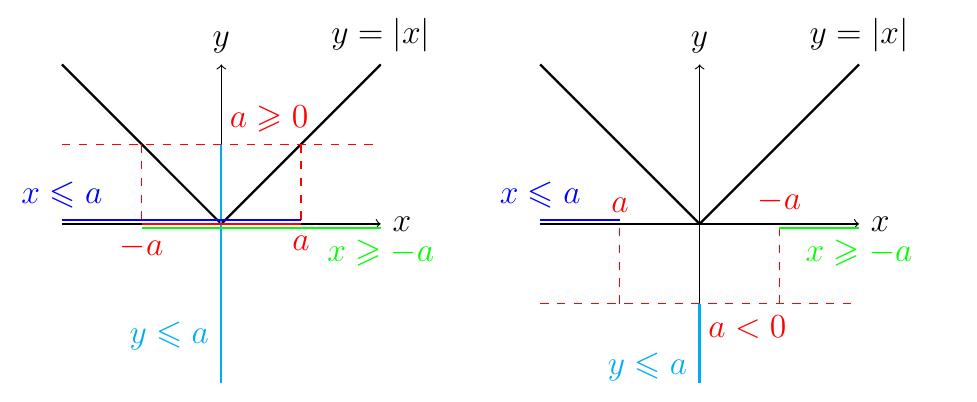
Si \(a\lt 0\), alors il n'existe aucun \(x\) qui satisfait à la fois \(x\leqslant a\lt 0\) et \(x\geqslant -a \gt 0\). Il n'y a donc pas besoin d'inclure de condition de positivité (''\(a\geqslant 0\)'') dans la résolution de l'inéquation.

En résumé, l'ensemble solution de l'inéquation \(|x|\leqslant a\) est

  1. \(S= [-a,a]\) si \(a\geqslant 0\),
  2. \(S=\varnothing\) si \(a \lt 0\).
L'inéquation \(|x|\geqslant a\)

L'équation \(|x|\geqslant a\), \(a\in\mathbb{R}\), admet évidemment tout \(x\in\mathbb{R}\) comme solution si \(a\lt 0\), une valeur absolue étant toujours plus grande qu'un nombre négatif. Il n'est donc pas nécessaire de discuter le signe de \(a\)!

Théorème: Soit \(a\in\mathbb{R}\). On a l'équivalence \[ |x|\geqslant a \qquad\Leftrightarrow \qquad \left\{ \begin{array}{l} x\geqslant a \\ \hspace{-3mm}\text{\scriptsize ou} \\ x\leqslant-a\,.\end{array} \right.\]

Similairement à l'inéquation précédente, on constate qu'il n'y a pas besoin de discuter du signe de \(a\). En effet, \(a\lt 0\) signifie que l'inéquation admet une infinité de solutions, puisque dans ce cas \[ ]-\infty,-a] \cup [a,+\infty[=\mathbb{R}\,. \]

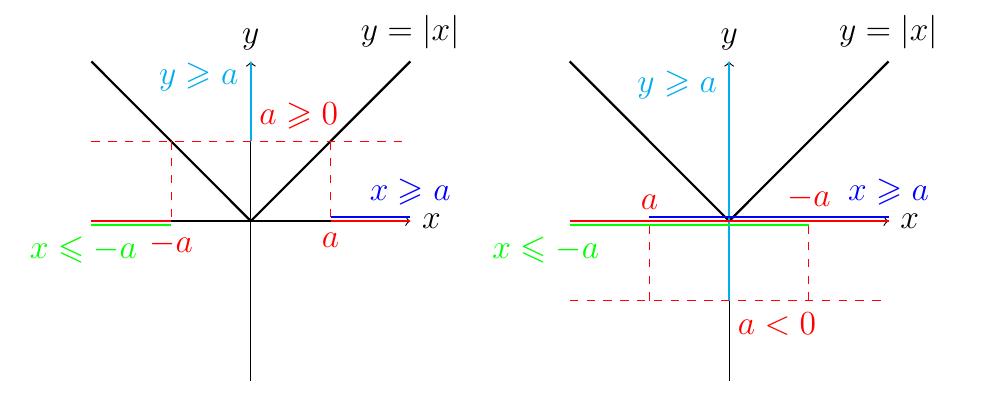
En résumé, l'ensemble solution \(S\) de l'équation \(|x|\geqslant a\) est donné par

  1. \(S=]-\infty,-a] \cup [a,+\infty[\) si \(a\geqslant 0\),
  2. \(S=\mathbb{R}\) si \(a\lt 0\).

Équations à valeurs absolues

L'équivalence vue plus haut, \[ |x|=a \qquad \Leftrightarrow \qquad a\geqslant 0 \text{ et } \left\{ \begin{array}{l} x=a \\ \hspace{-3mm}\text{\scriptsize ou} \\ x=-a\,. \end{array} \right. \] peut se généraliser au cas où \(x\) et \(a\) deviennent des fonctions.

Soient \(f\) et \(g\) deux fonctions réelles. Pour \(x\in D_\text{déf,f}\cap D_\text{déf,g}=D_\text{déf}\), on a l'équivalence \[ |f(x)|=g(x) \qquad \Leftrightarrow \qquad g(x)\geqslant 0 \quad \text{ et } \quad \left\{ \begin{array}{l} f(x)=g(x) \\ \hspace{-3mm}\text{\scriptsize ou} \\ f(x)=-g(x)\,.\end{array} \right. \]

Remarque: On ne discute que le signe de \(g(x)\) (condition de positivité), et pas celui de \(f(x)\). On doit donc résoudre l'équation \(|f(x)|=g(x)\) sur \(D_\text{déf} \cap D_\text{pos}\), où \[D_\text{pos} = \left\{ x\in D_\text{déf} \,|\, g(x) \geqslant 0 \right\}.\]

Exemple: Résolvons, en \(x\in\mathbb{R}\), l'équation \[|x^2+2x-5| = x+1\,.\] Sur \(D_\text{déf}=\mathbb{R}\), l'équation \(|x^2+2x-5|=x+1\) est équivalente à \[ x+1\geqslant 0 \quad \text{ et } \quad \left\{ \begin{array}{ll} x^2+2x-5=x+1&(1) \\ \hspace{-3mm}\text{\scriptsize ou} \\ x^2+2x-5=-(x+1)\,.&(2)\end{array} \right. \] La condition de positivité \(x+1\geqslant 0\) donne \(D_\text{pos}=[-1,+\infty[\).

  1. Résolvons (1) sur \(D_\text{déf}\cap D_\text{pos}= [\,-1,+\infty[\): \[ x^2+x-6=0 \qquad \Leftrightarrow \qquad (x+3)(x-2)=0\,, \] d'où \(S_1=\{2\}\). (On ne garde pas \(-3\), car hors du domaine de positivité: \(-3\notin[-1,+\infty[\).)
  2. Résolvons (2) sur \(D_\text{déf}\cap D_\text{pos}\): \[x^2+3x-4=0 \qquad \Leftrightarrow \qquad (x+4)(x-1)=0\,, \] d'où \(S_2=\{1\}\). (On ne garde pas \(-4\), car hors du domaine de positivité: \(-4\notin[-1,+\infty[\).)
En résumé, \(S=S_1\cup S_2=\{1,2\}\).

Exemple: Résolvons en \( x\in\mathbb{R}\) l'équation \[|x-3m+4|=x+m\,,\] où le paramètre \(m\in\mathbb{R}\). Sur \(D_\text{déf} = \mathbb{R}\), la condition de positivité est \[ D_\text{pos} = \left\{x \,|\, x+ m\geqslant0 \right\} = [-m,+\infty[\,, \] ce qui donne \(D_\text{déf}\cap D_\text{pos}=[-m,+\infty[\).

Ensuite, sur \(D_\text{déf}\cap D_\text{pos}\), on résout \(|x-3m+4|=x+m\), qui s'exprime par \[ \left\{ \begin{array}{ll} x-3m+4=x+m&(1) \\ \hspace{-3mm}\text{\scriptsize ou} \\ x-3m+4=-x-m\,.&(2)\end{array} \right. \]

  1. Résolvons (1) sur \(D_\text{déf}\cap D_\text{pos}\): \[x-3m+4=x+m \qquad \Leftrightarrow \qquad 0\cdot x = 4(m-1) \] On discute les cas :
    • Si \(m=1\) alors l'équation devient \(0\cdot x=0\), qui est satisfaite pour tout \(x\in \mathbb{R}\), donc en ne gardant que ce qui est dans \(D_\text{déf}\cap D_\text{pos}\), on obtient \(S_1 = [-1,+\infty[\).
    • Si \(m\neq 1\) alors l'équation devient \[0\cdot x = \underbrace{4(m-1)}_{\neq 0}\,,\] qui n'a aucune solution, et donc \(S_1 = \varnothing\).
  2. Résolvons ensuite (2) sur \(D_\text{déf}\cap D_\text{pos}\), \[x-3m+4=-x-m \qquad \Leftrightarrow \qquad x = (m-2) \,,\] dont la solution est \(x=m-2\). Mais on ne veut garder cette solution que si elle appartient à \(D_\text{déf}\cap D_\text{pos}\), c'est-à-dire si \[\begin{aligned} m-2\in [-m,+\infty[ &\qquad \Leftrightarrow \qquad m-2\geqslant -m\\ &\qquad \Leftrightarrow \qquad m \geqslant 1\,. \end{aligned}\] On a donc:
    • Si \(m\geqslant 1\), alors \(S_2=\left\{m-2\right\}\).
    • Si \(m \lt 1\), alors \(S_2=\varnothing\).
Finalement on résume la discussion en prenant l'ensemble solution \(S=S_1\cup S_2\) en fonction de \(m\): \[ S= \begin{cases} \varnothing & \text{ si } m\lt 1\,,\\ [-1,+\infty[ &\text{ si } m=1\,,\\ \left\{ m-2\right\} &\text{ si } m \gt 1\,. \end{cases} \] On observe ces solutions sur l'animation ci-dessous. En bleu, l'ensemble des solutions \(x\in S\), donnant l'ensemble des points où le graphe de \(|x-m+4|\) coupe la droite \(x+m\):

Inéquations \(|f(x)|\leqslant g(x)\)

On va ensuite généraliser l'inéquation \[ |x| \leqslant a \qquad \Leftrightarrow \qquad \left\{ \begin{array}{l} x\leqslant a \\ \hspace{-3mm}\text{\scriptsize et} \\ x\geqslant-a\end{array} \right. \] au cas où \(x\) et \(a\) sont remplacés par des fonctions de \(x\).

Soient \(f\) et \(g\) deux fonctions réelles. Pour \(x\in D_\text{déf,f}\cap D_\text{déf,g}=D_\text{déf}\), on a l'équivalence \[|f(x)|\leqslant g(x) \qquad \Leftrightarrow \qquad \left\{ \begin{array}{l} f(x)\leqslant g(x) \\ \hspace{-3mm}\text{\scriptsize et} \\ f(x)\geqslant-g(x)\,.\end{array} \right. \] Comme déjà expliqué, il n'est pas nécessaire de discuter du signe de \(g(x)\).

Remarque: L'équivalence reste vraie en remplaçant les inégalités larges par les inégalités strictes.

Exemple: Résolvons, en \(x\in\mathbb{R}\), l'inéquation \[|x| + \frac{x-1}{2} \lt 0\,.\] Sur \(D_\text{déf}=\mathbb{R}\), \[ |x| \lt -\frac{x-1}{2} \qquad \Leftrightarrow \qquad \left\{ \begin{array}{ll} x \lt -\frac{x-1}{2}&(1) \\ \hspace{-3mm}\text{\scriptsize et} \\ x \gt \frac{x-1}{2}\,.&(2)\end{array} \right.\]

  1. Résolvons (1) sur \(D_\text{déf}\): \(3x\lt 1\) et donc \(S_1=]-\infty,\frac{1}{3}[\).
  2. Résolvons (2) sur \(D_\text{déf}\): \(x \gt -1\), et donc \(S_2=]-1,+\infty[\).
En conclusion, \[ S =S_1\cap S_2 =]-1,\tfrac{1}{3}[\,. \]

Exemple: Résolvons, en \(x\in\mathbb{R}\), l'inéquation \[ \vert x-m \vert -1 \lt 2x\,,\] où le paramètre \(m\in\mathbb{R}\).

Sur \(D_\text{déf}=\mathbb{R}\), \[|x-m| \lt 2x+1 \qquad \Leftrightarrow \qquad \left\{ \begin{array}{ll} x-m \lt 2x+1 &(1) \\ \hspace{-3mm}\text{\scriptsize et} \\ x-m \gt -2x-1\,.&(2) \end{array} \right.\]

  1. Résolvons (1) sur \(D_\text{déf}\): \(-m-1 \lt x\), d'où \(S_1=]-m-1,+\infty\,[\).
  2. Résolvons (2) sur \(D_\text{déf}\): \(3x \gt m-1\), d'où \(S_2=\left] \frac{m-1}{3},+\infty\right[\).
Pour pouvoir conclure, il faut calculer \(S=S_1 \cap S_2\). Or cette intersection va dépendre de \(m\), et pour le comprendre, il faut quel intervalles, \(S_1\) ou \(S_2\), a son extrémité gauche plus petite que celle de l'autre. On peut donc par exemple regarder quand \(S_2\) a son extrémité gauche inférieure à celle de \(S_1\): \[-m-1 \geqslant \frac{m-1}{3} \qquad \Leftrightarrow \qquad m \leqslant -\frac{1}{2}.\] On peut donc conclure que Graphiquement, l'animation ci-dessous permet de vérifier que l'ensemble \(S\) décrit bien les points pour lesquels le graphe de \(y=|x-m|-1\) est au-dessous de la droite \(y=2x\):

Inéquations \(|f(x)|\geqslant g(x)\)

On va ensuite généraliser l'inéquation \[|x|\geqslant a \qquad \Leftrightarrow \qquad \left\{ \begin{array}{l} x\geqslant a \\ \hspace{-3mm}\text{\scriptsize ou} \\ x\leqslant-a\end{array} \right. \] au cas où \(x\) et \(a\) sont remplacés par des fonctions de \(x\).

Soient \(f\) et \(g\) deux fonctions réelles. Pour \(x\in D_\text{déf,f}\cap D_\text{déf,g}=D_\text{déf}\), on a l'équivalence \[ |f(x)|\geqslant g(x) \qquad \Leftrightarrow \qquad \left\{ \begin{array}{l} f(x)\geqslant g(x) \\ \hspace{-3mm}\text{\scriptsize ou} \\ f(x)\leqslant-g(x)\,.\end{array} \right.\]

Remarque: L'équivalence reste vraie en remplaçant les inégalités larges par les inégalités strictes.

Exemple: Résolvons, en \(x\in\mathbb{R}\), l'inéquation \[|x-2| \gt \frac{2x-4}{x}\,.\] Sur \(D_\text{déf}=\mathbb{R}^\ast\), on a \[ |x-2| \gt \frac{2x-4}{x} \qquad \Longleftrightarrow \qquad \left\{ \begin{array}{ll} x-2 \gt \frac{2x-4}{x}&(1) \\ \hspace{-3mm}\text{\scriptsize ou} \\ x-2 \lt -\frac{2x-4}{x}\,.&(2)\end{array} \right. \]

  1. Résolvons (1) sur \(D_\text{déf}\): \[x-2 - \frac{2x-4}{x} \gt 0 \qquad \Longleftrightarrow \qquad \frac{(x-2)^2}{x} \gt 0 \,, \] d'où \(S_1=\mathbb{R}_+^\ast \setminus \{2\}\).
  2. Résolvons (2) sur \(D_\text{déf}\): \[x-2 + \frac{2x-4}{x} \lt 0 \qquad \Longleftrightarrow \qquad \frac{(x-2)(x+2)}{x}\lt 0 \] Tableau des signes: \[\begin{array}{c|ccccccccccc} x & &-2& &0& &2& \\ \hline x-2 &-&0&+&+&+&+&+ \\ x+2 &-&-&-&-&-&0&+ \\ x &-&-&-&0&+&+&+ \\\hline (x-2)(x+2)/x & -&0&+&\Vert&- &0&+ \end{array}\] D'où \(S_2=\:]-\infty,\,-2\,[ \,\cup\, ]\,0\,,\,2\,[\).
On a ainsi comme ensemble solution: \[S = S_1 \cup S_2 = ]-\infty,-2[ \cup ]0,2[ \cup ]2,+\infty[\,. \]

Dernière compilation: 2025-06-01 (06:48:33)

Sauf indication contraire, le contenu de ce document est soumis à une licence Creative Commons internationale, Attribution: Pas d'Utilisation Commerciale - Partage dans les Mêmes Conditions 4.0 (CC BY-NC-SA 4.0)