2.6 Équations et inéquations avec racines
Racines positives (ou arithmétiques)
Soient \(a\in\mathbb{R}_+\) et \(n\in\mathbb{N}^\ast\). Le réel positif \(x\) vérifiant \[x^n=a\] est appelé racine \(n^\text{ème}\) positive de \(a\). Il est noté \(x=\sqrt[n]{a}\).

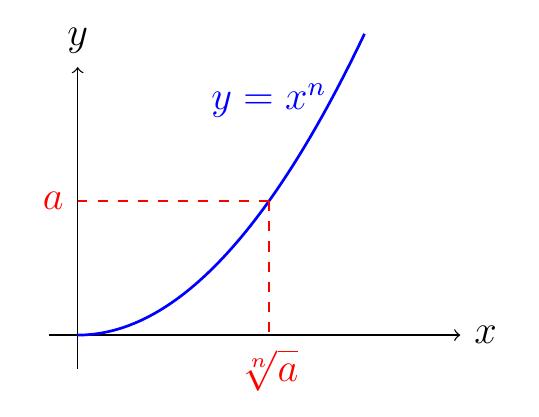
La racine \(2^{\text{ème}}\), appelée racine carrée, est notée \(\sqrt{a}\) (au lieu de \(\sqrt[2]{a}\)).

Exemple:

Soient \(a,b\in\mathbb{R}_+\), \(m,n\in\mathbb{N}^\ast\).
  1. \(\left(\sqrt[n]{a}\right)^n = a\).
  2. \(\sqrt[n]{a^m} = \left(\sqrt[n]{a}\right)^m\).
  3. \(\sqrt[n]{ab} = \sqrt[n]{a}\sqrt[n]{b}\).
  4. \(\sqrt[m]{ \sqrt[n]{a} } = \sqrt[mn]{a}\).

1. est juste une reformulation de la définition. Les autres propriétés découlent des propriétés des puissances entières.

  • Si on pose \(x=(\sqrt[n]{a})^m\), alors \[x^n= \left((\sqrt[n]{a})^m\right)^n= \left(\sqrt[n]{a}\right)^{mn}= \left((\sqrt[n]{a})^n\right)^m=a^m\,, \] ce qui signifie bien que \(x=\sqrt[n]{a^m}\).
  • Si on pose \(x=\sqrt[n]{a}\sqrt[n]{b}\), alors \[ x^n= \left(\sqrt[n]{a}\sqrt[n]{b}\right)^n= \left(\sqrt[n]{a}\right)^n \left(\sqrt[n]{b}\right)^n=ab\,, \] ce qui signifie bien que \(x=\sqrt[n]{ab}\).
  • Si on pose \(x=\sqrt[m]{\sqrt[n]{a}}\), alors \[ x^{mn}= \left(\sqrt[m]{\sqrt[n]{a}}\right)^{mn}= \left((\sqrt[m]{\sqrt[n]{a}})^m\right)^{n}= (\sqrt[n]{a})^n=a\,, \] ce qui signifie bien que \(x=\sqrt[mn]{a}\).

Remarque: Les propriétés usuelles des puissances restent valables en posant \[\sqrt[q]{a^p} = a^{\frac{p}{q}} \quad a\in\mathbb{R}^\ast_+, p\in\mathbb{Z}, q\in\mathbb{N}^\ast \,.\]

Exemple: \(\displaystyle 7^{-\frac{2}{3}} = \frac{1}{\sqrt[3]{7^2}},\; \sqrt{3x^2} = |x|\sqrt{3}\,.\)

Racines réelles
Soient \(a\in\mathbb{R}\) et \(n\in\mathbb{N}^\ast\). Un nombre \(x\in\mathbb{R}\) est une racine \(n^\text{e}\) réelle de \(a\) si \(x\) vérifie \(x^n=a\).

Exemples:

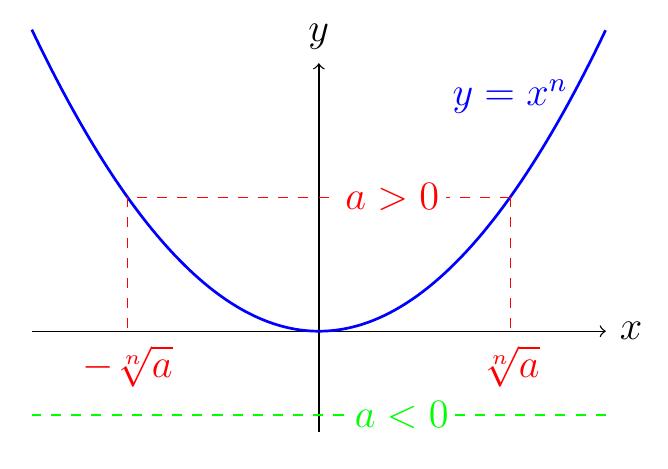
Discussion graphique des solutions en \(x\) à l'équation \(x^n=a\).

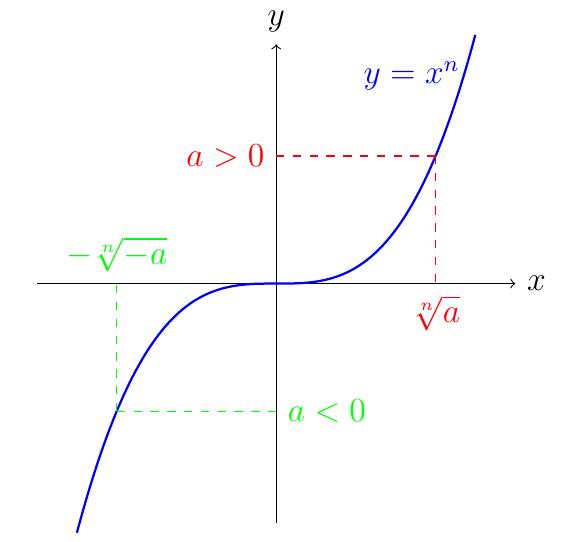
Dans le cas d'une puissance impaire, on peut donc étendre la racine \(n^\text{ème}\) aux réels négatifs:

Si \(a\in\mathbb{R}_-\) et \(n\in\mathbb{N}^\ast\) est impair, on définit \(\sqrt[n]{a}:=-\sqrt[n]{-a}\).

Cette dernière donne bien la racine \(n^\text{ème}\) négative de \(a\), puisque \[ \left(-\sqrt[n]{-a}\right)^n=-\sqrt[n]{-a}^n=-(-a)=a\,. \]

Exemples:

Conséquences:

En particulier, et sera utilisé pour résoudre des équations à racines carrées: \[a^2 = b^2 \Leftrightarrow a=b \text{ si et seulement si } a \text{ et } b \text{ sont de même signes}\] et \[ a^2 \lt b^2 \Leftrightarrow a \lt b \text{ si et seulement si } a \text{ et } b \text{ sont positifs ou nuls.}\]

Equations avec racine carrée

Commençons par considérer une équation du type \[ \sqrt{f(x)}=g(x)\,, \qquad x\in D_\text{déf}\,. \] La racine carrée étant définie seulement sur les positifs, on a \[D_\text{déf} = \left\{x\in \mathbb{R}\,|\,f(x) \text{ et } g(x) \text{ sont définis, et } f(x) \geqslant 0 \right\}. \] Pour résoudre l'équation, on aimerait élever au carré pour ne plus avoir de racine. Mais puisque l'équivalence \[ \sqrt{f(x)}=g(x) \quad\Leftrightarrow\quad \sqrt{f(x)}^2 = g(x)^2 \] n'est vraie que si \(\sqrt{f(x)}\) et \(g(x)\) sont de même signes, et puisque \(\sqrt{f(x)}\), lorsqu'il est bien défini, est toujours positif, on doit donc introduire une condition de positivité: \[D_\text{pos} = \left\{ x \in \mathbb{R} \,|\, g(x) \geqslant 0 \right\}.\] On a donc:

Théorème: Soient \(f\) et \(g\) deux fonctions réelles. Pour \(x\in D_\text{déf}\), on a l'équivalence \[\sqrt{f(x)}=g(x) \quad \Longleftrightarrow \quad g(x)\geqslant 0 \text{ et } f(x)=g^2(x) \,.\]

Exemple: Résolvons l'équation \[\sqrt{x^2-3x+6} = 4x-6\,. \] Comme le discriminant de \(x^2-3x+6\) est \(\Delta=-15\lt 0\) et comme le coefficient devant \(x^2\) est \(1\) (strictement positif), on a que \[ D_\text{déf}=\{x\in\mathbb{R}\,|\,x^2-3x+6\geqslant 0\}=\mathbb{R}\,. \] Ecrivons la condition de positivité: \(4x-6\geqslant 0 \Leftrightarrow x\geqslant \frac{3}{2}\), d'où \[ D_\text{pos}=\left[\tfrac{3}{2},+\infty \right[\,. \] Sous la condition de positivité, on peut élever les deux membres au carré. Sur \(D_\text{pos}\cap D_\text{déf}\), l'équation de départ est donc équivalente à \[\begin{aligned} x^2-3x+6 &= (4x-6)^2 \\ &= 16x^2-48x+36 \end{aligned}\] En regroupant les termes de mêmes degrés, celle-ci devient \[\begin{aligned} 15 x^2-45x+30 = 0 &\quad\Leftrightarrow\quad x^2-3x+2 = 0\\ &\quad\Leftrightarrow\quad (x-1)(x-2) = 0 \\ &\quad\Leftrightarrow\quad x=1 \text{ ou }x=2\,. \end{aligned}\] Comme \(1\not\in D_{\text{pos}}\), on conclut: \(S= \{2\}\).

Remarquons qu'en effet, \(x=1\) n'est pas solution puisque \[ \underbrace{\sqrt{1^2-3\cdot 1+6}}_{=2} \neq \underbrace{4\cdot 1-6}_{=-2} \]

Exemple: Résolvons l'équation \[ \sqrt{x+m^2} = x+m\,, \] en fonction du paramètre réel \(m\).

D'abord, \[ D_\text{déf}=\{x\in\mathbb{R}\,|\,x+m^2\geqslant 0\}=\left[-m^2,+\infty \right[\,, \] et \[D_\text{pos}=\{x\in\mathbb{R}\,|\,x+m\geqslant 0\}=\left[-m,+\infty \right[\,. \] Sur \(D_\text{déf}\cap D_\text{pos}\), l'équation de départ est équivalente à \[\begin{aligned} x+m^2 &= (x+m)^2 \\ &= x^2+2mx+m^2 \end{aligned}\] Si on regroupe les termes de mêmes degrés, \[\begin{aligned} x^2+(2m-1)x = 0 &\quad \Leftrightarrow \quad x(x+2m-1)=0 \\ &\quad \Leftrightarrow \quad x=0 \text{ ou }x=1-2m \end{aligned}\] Voyons maintenant, en fonction de \(m\), si ces nombres sont effectivement solutions de l'équation, c'est-à-dire appartiennent à \(D_\text{déf}\cap D_\text{pos}\). Pour la première,

Donc \(0\) est solution si et seulement si \(m\geqslant 0\). Donc \(1-2m\) est solution si et seulement si \(m\leqslant 1\).

En résumé, \[ S= \begin{cases} \{1-2m\} & \text{ si }m\lt 0\,,\\ \{0,1-2m\} & \text{ si }m\in [0,1]\,,\\ \{0\} & \text{ si }m\gt 1\,. \end{cases} \] On observe la dépendance de \(S\) sur l'animation ci-dessous, en regardant où la courbe \(y=\sqrt{x+m^2}\) coupe la droite \(y=x+m\), en fonction de \(m\):

Inéquations avec racine carrée

Tout comme dans une équation, on cherchera dans une inéquation contenant une racine carrée à élever au carré pour se débarrasser de la racine. Il convient cependant de prendre quelques précautions, l'équivalence \(a\leqslant b \Leftrightarrow a^2\leqslant b^2\) n'étant vraie que pour \(a,b\geqslant 0\). Le domaine de définition est le même que dans le cas des équations.

Théorème: Soient \(f\) et \(g\) deux fonctions réelles. Pour \(x\in D_\text{déf}\), on a les équivalences \[\begin{aligned} \sqrt{f(x)}\leqslant g(x) &\quad\Longleftrightarrow\quad g(x)\geqslant 0 \text{ et } f(x)\leqslant g^2(x)\,,\\ \sqrt{f(x)}\lt g(x) &\quad\Longleftrightarrow\quad g(x) \geqslant 0 \text{ et } f(x)\lt g^2(x) \,. \end{aligned}\]

En effet, dans le premier cas, si \(g(x) \lt 0\), l'inéquation ne peut avoir de solution puisque \(\sqrt{f(x)}\) est toujours positif. Ainsi, si la condition de positivité \(g(x)\geqslant 0\) est satisfaite, les deux membres de l'inéquation sont positifs et la mise au carré conduit au même ensemble solution.

Exemple: Résolvons \[ \sqrt{6-x} \leqslant 3+2x\,. \] D'abord, \(D_\text{déf}=\{x\in\mathbb{R}\,|\,6-x\geqslant 0\}=]-\infty,6]\). On a donc, sur \(D_\text{déf}\), l'équivalence \[\sqrt{6-x} \leqslant 3+2x \quad \Longleftrightarrow \quad 3+2x \geqslant 0 \text{, et } 6-x \leqslant (3+2x)^2\,.\] La condition de positivité \(x\geqslant -\frac{3}{2}\) donne \(D_\text{pos}=[-\frac{3}{2},+\infty[\). Sur \(D_\text{pos}\cap D_\text{déf}=[-\frac32,6]\), on peut maintenant résoudre \[\begin{aligned} 6-x \leqslant 9+12x+4x^2 \quad & \Leftrightarrow \quad 4x^2+13x+3 \geqslant 0 \\ &\Leftrightarrow \quad (4x+1)(x+3)\geqslant 0 \\ &\Leftrightarrow \quad x\in ]-\infty,-3] \cup [-\tfrac{1}{4},+\infty[\,. \end{aligned}\] En ne gardant que les éléments qui sont dans \(D_\text{pos}\cap D_\text{déf}=[-\frac32,6]\), on a donc: \(S=\:\left[\,-\tfrac{1}{4}\,,\,6\,\right]\).

Théorème: Soient \(f\) et \(g\) deux fonctions réelles. Pour \(x\in D_\text{déf}\),, on a les équivalences \[\begin{array}{rcl} \sqrt{f(x)}\geqslant g(x) &\Longleftrightarrow& \left\{ \begin{array}{l} g(x)\lt 0 \\ \hspace{-3mm}\text{\scriptsize ou} \\ g(x)\geqslant 0 \text{ et } f(x)\geqslant g^2(x)\end{array} \right. \\ \\ \sqrt{f(x)}\gt g(x) &\Longleftrightarrow& \left\{ \begin{array}{l} g(x)\lt 0 \\ \hspace{-3mm}\text{\scriptsize ou} \\ g(x)\geqslant 0 \text{ et } f(x)\gt g^2(x)\end{array} \right.\,. \end{array}\]

En effet, si \(x\) est tel que \(g(x) \lt 0\), alors l'inéquation est vérifiée puisque \(\sqrt{f(x)}\geqslant 0\). C'est donc une partie de la solution. D'un autre côté, pour les \(x\) tels que \(g(x)\geqslant 0\) les deux membres de l'inéquation sont positifs et la mise au carré conduit au même ensemble solution, sous la restriction \(g(x)\geqslant 0\). C'est l'autre partie de la solution.

Exemple: Résolvons l'inéquation \[ \sqrt{-x^2-x+6} \geqslant x+1\,. \] D'abord, \[ D_\text{déf} =\{x\in\mathbb{R}\,|\,-x^2-x+6\geqslant 0 \} =[-3,2]\,. \] Sur \(D_\text{déf}\), on a \[\begin{aligned} \sqrt{-x^2-x+6} &\geqslant x+1 \\ \Longleftrightarrow & \quad \left\{ \begin{array}{ll} x+1 \lt 0&(1) \\ \hspace{-3mm}\text{\scriptsize ou} \\ x+1 \geqslant 0 \quad\text{et}\; -x^2-x+6 \geqslant (x+1)^2\,.&(2) \end{array} \right. \end{aligned}\] Les solutions de (1) sont \(x\lt -1\), et en ne gardant que celles dans \(D_\text{déf}\), on obtient \(S_1=\:[-3,\,-1\,[\).

Pour résoudre (2), on peut inclure la condition de positivité, \(x\geqslant -1\) dans \(D_\text{pos}=[-1,+\infty[\), puis résoudre \[\begin{aligned} -x^2-x+6 \geqslant x^2+2x+1 \quad&\Leftrightarrow \quad 2x^2+3x-5 \leqslant 0 \\ &\Leftrightarrow \quad (2x+5)(x-1)\leqslant 0 \\ &\Leftrightarrow \quad x \in [-\tfrac{5}{2},1] \end{aligned}\] Ainsi, en ne gardant que les \(x\) qui sont aussi dans \(D_\text{déf}\cap D_\text{pos}=[-1,2]\), on a \(S_2=[-1,1]\).

Pour conclure: \(S=S_1 \cup S_2 = \left[-3,1\right]\).

Dernière compilation: 2025-06-01 (06:48:34)

Sauf indication contraire, le contenu de ce document est soumis à une licence Creative Commons internationale, Attribution: Pas d'Utilisation Commerciale - Partage dans les Mêmes Conditions 4.0 (CC BY-NC-SA 4.0)