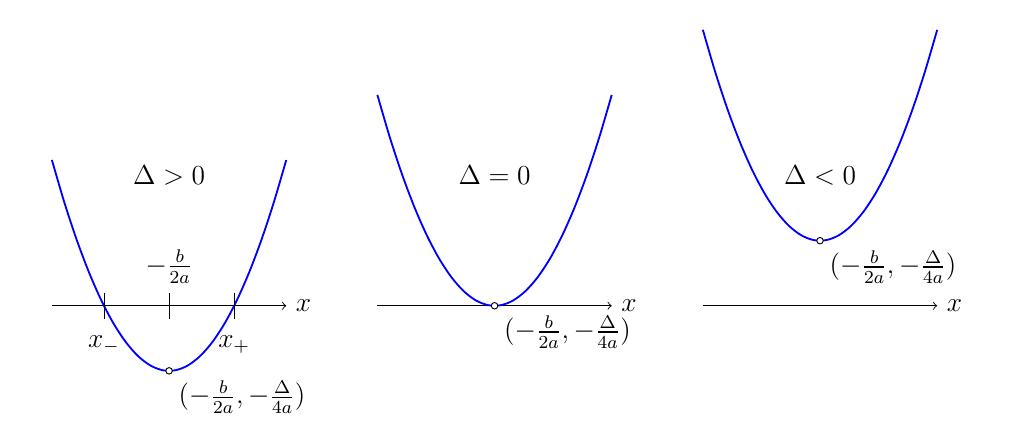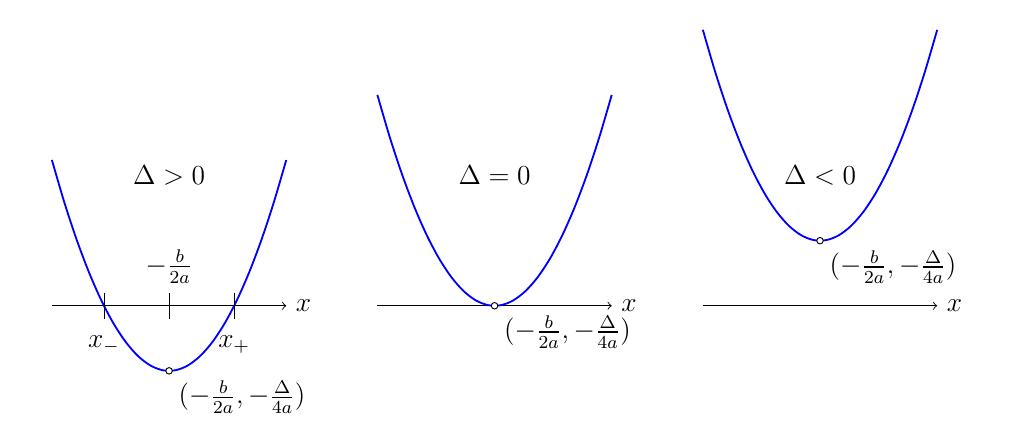2.4 Équations et inéquations du deuxième degré
Soient \(a,b,c\in\mathbb{R}\), avec \(a\neq 0\). On appelle
\[
p(x)=ax^2+bx+c
\] un trinôme du deuxième degré en \(x\), et
\[
p(x)=0
\]
est une équation quadratique en \(x\in\mathbb{R}\).
Avant d'étudier les solutions d'une équation quadratique, remarquons que l'on
peut écrire, puisque \(a\neq 0\),
\[\begin{aligned}
p(x)
&=ax^2 + bx+c \\
&=a\left( x^2 +2\frac{b}{2a}x + \frac{c}{a}\right) \\
&=a\left(x^2 + 2\frac{b}{2a}x {\color{blue}+ \frac{b^2}{(2a)^2} -
\frac{b^2}{(2a)^2}} + \frac{c}{a}\right) \\
&=a\left[\left(x+\frac{b}{2a}\right)^2 - \frac{b^2-4ac}{4a^2}\right]\,.
\end{aligned}\]
(Dans la troisième ligne, on a complété le carré.)
Si \(b^2-4ac\) est positif, l'expression entre crochets peut être factorisée.
\(\Delta = b^2-4ac\) est appelé le discriminant du trinôme
\(p(x)=ax^2+bx+c\), \(a,b,c\in\mathbb{R},\,a\neq0\).
Si \(b=2b'\), \(\Delta' = b'^2-ac\) est appelé le
discriminant réduit du
trinôme \(p(x)=ax^2+2b'x+c\), \(a,b',c\in\mathbb{R},\,a\neq0\).
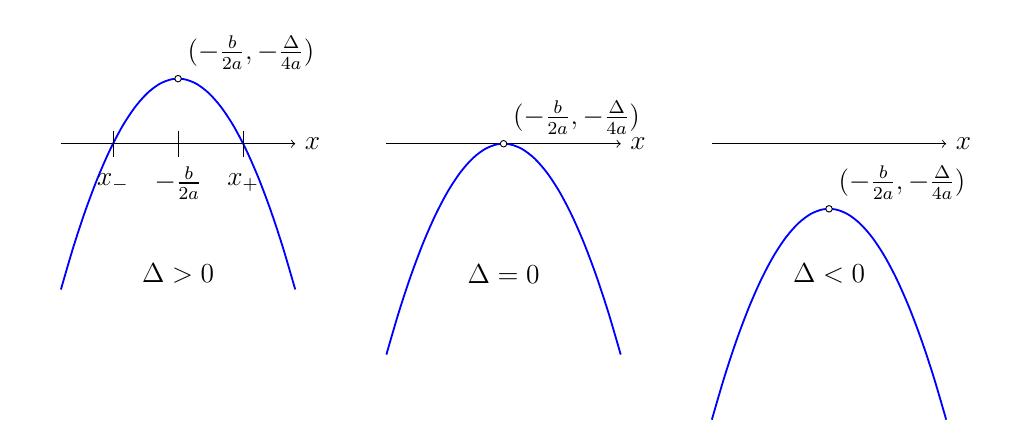
Signe du trinôme
- Cas \(\Delta\gt 0\): On peut écrire \(\Delta=\sqrt{\Delta}^2\), et
donc
\[\begin{aligned}
p(x)
&=a\left[\left(x+\frac{b}{2a}\right)^2 -
\left(\frac{\sqrt{\Delta}}{2a}\right)^2\right]\\
&= a \left(x+\frac{b}{2a} - \frac{\sqrt{\Delta}}{2a}\right)
\left(x+\frac{b}{2a} + \frac{\sqrt{\Delta}}{2a}\right) \\
&= a\bigl(x-x_+\bigr)\bigl(x-x_-\bigr)
\end{aligned}\]
où
\[x_{\pm}=\frac{-b\pm\sqrt{\Delta}}{2a}\]
sont les deux racines
(ou zéros)
distinctes de \(p(x)\).
Remarquons que \(x_-\lt x_+\).
Donc dans le cas \(\Delta\gt 0\), l'équation \(p(x)=0\) possède deux solutions
distinctes: \(S=\{x_-,x_+\}\).
Remarque:
Si \(b=2b'\), \(x_{\pm} = \displaystyle \frac{-b'\pm\sqrt{\Delta'}}{a}\,.\)
- \(\mathrm{sgn} (p(x))=\mathrm{sgn}(a)\) pour tout \(x\in\:]-\infty,x_-[ \cup ]x_+,+\infty[\)
- \(\mathrm{sgn} (p(x))=-\mathrm{sgn}(a)\) pour tout \(x\in ]x_-,x_+[\)
- Cas \(\Delta=0\): Dans ce cas,
\[p(x)=a\left(x+\frac{b}{2a}\right)^2\,.\]
Les deux racines de \(p(x)\) sont confondues,
\[x_-=x_+=-\frac{b}{2a}\,,\]
et la discussion du signe de \(p(x)\) est immédiate:
\[\mathrm{sgn} (p(x))
= \mathrm{sgn}(a) \quad \forall\,x\in\mathbb{R}\setminus
\textstyle \left\{-\frac{b}{2a}\right\}\,.\]
- Cas \(\Delta\lt 0\): Dans ce cas,
\(p(x)\) n'a pas de racine réelle, et
\[ \mathrm{sgn} (p(x)) = \mathrm{sgn}(a) \quad \forall\, x \in\mathbb{R}\,. \]
Remarque:
La discussion du signe de \(p(x)\) est la même avec \(\Delta'\).
Remarque:
Si \(x_-\) et \(x_+\) sont deux racines (distinctes ou confondues) du
trinôme \(p(x)=ax^2+bx+c\), alors
\[\begin{aligned}
x_-+x_+ &= -\frac{b}{a} \\
x_-\cdot x_+ &= \frac{c}{a} \,.
\end{aligned}\]
On appelle ces dernières les formules de Viète.
Représentation graphique
Considérons le graphe de \(p\), c'est-à-dire l'ensemble des points
\((x,y)\) du plan vérifiant \(y=p(x)=ax^2+bx+c\):
\[
\Gamma:\quad \{(x,y)\in\mathbb{R}^2\,:\,x\in\mathbb{R},\,y=p(x)\}\,.
\]
Puisque l'on suppose \(a\neq 0\), on appelle \(\Gamma\) une parabole.
En utilisant la factorisation
de \(p(x)\) obtenue plus haut,
\[
y= a\left( x+\frac{b}{2a}\right)^2-\frac{\Delta}{4a}\,,
\]
on conclut que
\(\Gamma\) s'obtient à partir de la parabole élémentaire \(y=x^2\) par
- translation horizontale (selon \(x\)) de \(-\frac{b}{2a}\)
- amplification (multiplication) verticale par \(a\)
- translation verticale (selon \(y\)) de \(-\frac{\Delta}{4a}\).
Ceci permet d'en déduire les propriétés suivantes:
- \(\Gamma\) possède un axe de symétrie, vertical,
d'équation \(x=-\frac{b}{2a}\).
-
Les coordonnées du sommet \((x_s,y_s)\) de \(\Gamma\) sont
\[x_s=-\frac{b}{2a} \qquad y_s=-\frac{\Delta}{4a}\,.\]
- Les intersections de \(\Gamma\) avec
l'axe des \(x\) sont données par les racines (s'il y en a) de \(p(x)\).
- Si \(a \gt 0\): \(\Gamma\) est tournée vers le haut
(les branches infinies vont vers les \(y\) positifs) et
\(p(x)\) admet un minimum.
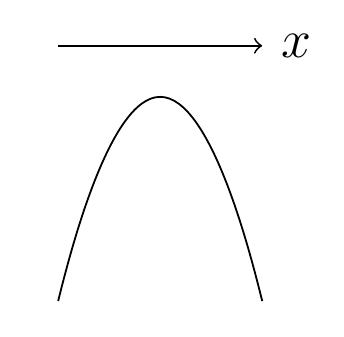
- Si \(a \lt 0\): \(\Gamma\) est tournée vers le bas
(les branches infinies vont vers les \(y\) négatifs) et
\(p(x)\) admet un maximum.
Remarque:
L'abscisse du sommet est bien la moyenne des racines:
\[
x_s
=\frac{x_-+x_+}{2}
=\frac{-b/a}{2}
=-\frac{b}{2a}\,.
\]
Exemples avec paramètre
Exemple:
Résoudre en \(x\in\mathbb{R}\) l'inéquation suivante,
en fonction du paramètre \(m\in\mathbb{R}\):
\[x^2-1 \leqslant m(x-1)\,,
\]
En regroupant et en factorisant, l'équation devient
\[
(x-1)(x+1)- m(x-1)\leqslant 0
\quad
\Leftrightarrow
\quad
(x-1)(x+1-m) \leqslant 0\,.
\]
Les racines du trinôme sont \(1\) et \(m-1\).
- Si \(1 \lt m-1 \Leftrightarrow m\gt 2\),
\(S=[\,1\,,\,m-1\,]\,.\)
- Si \(1=m-1 \Leftrightarrow m=2\),
\(S=\{1\}\,.\)
- Si \(1\gt m-1 \Leftrightarrow m\lt 2\),
\(S=[\,m-1\,,\,1\,]\,.\)
En résumé,
\[S =
\begin{cases}
[\,m-1\,,\,1\,] & \text{ si } m \lt 2\\
\{1\} & \text{ si } m = 2\\
[\,1\,,\,m-1\,] & \text{ si } m \gt 2\,.
\end{cases}\]
Si on interprète l'ensemble des solutions de \(x^2-1\leqslant m(x-1)\) comme étant
l'ensemble des abscisses \(x\) pour lesquelles la parabole \(y=x^2-1\) est
au-dessous de la droite \(y=m(x-1)\), on peut vérifier sur l'animation
ci-dessous que notre ensemble solution est le bon:
Exemple: Soit \(p\) le trinôme
\[
p(x)=kx^2-2(k+1)x+5-\frac{1}{k}\,.
\]
Déterminer les valeurs du paramètre \(k\in \mathbb{R}^*\) pour lesquelles
la parabole \(\Gamma\) (graphe de \(p\)) soit située strictement sous l'axe
\(Ox\).
Pour que \(\Gamma\) soit entièrement sous \(Ox\), il faut que
\(p(x)\lt 0\) pour tout \(x\in\mathbb{R}\). Cela signifie:
- Pas d'intersection avec \(Ox\): \(\Delta\lt 0\)
- \(\Gamma\) tournée vers le bas: coefficient devant \(x^2\) négatif, \(k\lt
0\).
Figure d'étude:
Regardons ce que ces conditions impliquent sur \(k\).
D'abord, si on tient compte de la présence de \(k\) dans les
coefficients du trinôme,
\[\begin{aligned}
\Delta
&= (-2(k+1))^2 - 4k(5-\tfrac{1}{k})\\
&= 4(k^2-3k+2)\\
&= 4(k-1)(k-2)
\end{aligned}\]
Les valeurs de \(k\) qui garantissent \(\Delta\lt 0\) (première condition
ci-dessus) sont donc \(k\in ]1,2[\).
Ensuite, on a vu que la deuxième condition impose \(k\lt 0\).
Comme on ne doit garder que les \(k\) qui satisfont aux deux conditions en même
temps, \(k\in ]1,2[\) et \(k\lt 0\). Comme ces deux conditions sont
incompatibles, on conclut qu'il n'y a aucun
\(k\) qui satisfait à la condition requise.
Effectivement, on vérifie sur l'animation ci-dessous qu'il n'y a pas de valeurs
de \(k\lt 0\) pour lesquelles la parabole
\(p(x)=kx^2-2(k+1)x+5-\frac{1}{k}\)
est entièrement sous l'axe \(O_x\):
(Il y a bien les valeurs de \(k\in ]1,2[\) pour lesquelles la parabole ne coupe pas
\(Ox\), mais ces valeurs sont positives...)
Exemple: Soit \(p\) le trinôme
\[
p(x)=mx^2-mx-(m+1)\,.
\]
Déterminer les valeurs de \(m\in\mathbb{R}^*\) pour lesquelles \(p(x)\) possède
deux racines distinctes \(x_-\) et \(x_+\)
vérifiant \(x_- \lt 1 \lt x_+\).
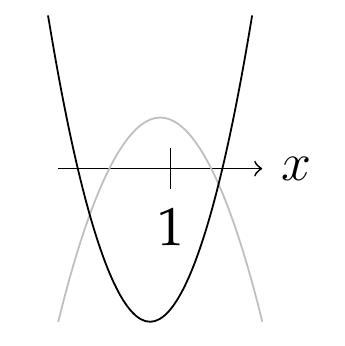
Figure d'étude:
1) la parabole doit doit couper \(Ox\) en deux points, et
2) \(x=1\) doit être entre ces deux points:
Détaillons les deux conditions ci-dessus.
- Pour couper \(Ox\) en deux points, il faut que
\(\Delta\gt 0\), où
\[\begin{aligned}
\Delta
&=(-m)^2 + 4 m (m+1) \\
&=m(5m+4)\,.
\end{aligned}\]
Donc l'ensemble des valeurs de \(m\) qui satisfont à la première condition est
\[S_a=]-\infty\,,\,-\tfrac{4}{5}\,[ \:\cup \:]\,0\,,\,+\infty[\]
- Pour que \(x=1\) se trouve entre les deux racines, il faut que
le coefficient de \(x^2\) soit opposé au signe de \(p(1)\), ou plus simplement
que leur produit soit strictement négatif:
\(m\cdot p(1) \lt 0\). Comme \(p(1)=m-m-(m+1)=-m-1\), la condition sur \(m\) est
donc \(-m (m+1) \lt 0\). Ainsi, l'ensemble des valeurs de \(m\) qui satisfont à
la deuxième condition est
\[S_b=\:]-\infty\,,\,-1\,[ \:\cup \:]\,0\,,\,+\infty[\]
Ainsi, l'ensemble des valeurs de \(m\) qui satisfont aux deux conditions en même
temps est
\[
S=S_a\cap S_b
=\:]-\infty\,,\,-1\,[ \:\cup \:]\,0\,,\,+\infty[\,.
\]
On peut vérifier le résultat sur l'animation ci-dessous: