3.9 Série géométrique et applications

Théorème: Soit \(r\in \mathbb{R}\), et, pour tout \(n\geqslant 1\), définissons la suite \[ s_n:= 1+r+r^2+r^3+\cdots +r^{n-1}+r^n\,. \] Dans la limite \(n\to \infty\),

Si \(r=1\), alors \[ s_n=1+1+1^2+1^3+\cdots+1^n=n+1\,, \] ce qui implique \(s_n\to+\infty\).

Si \(r\neq 1\), on a vu que \[ s_n=\frac{1-r^{n+1}}{1-r}\,. \] On peut alors considérer séparément les cas:

  • \(r\gt 1\). Dans ce cas, on écrit plutôt \[ s_n=\frac{r^{n+1}-1}{r-1}\,. \] Comme \(r-1\gt 0\) et \(r^{n+1}\to \infty\), on a \(s_n\to +\infty\).
  • \(-1\lt r\lt 1\). Dans ce cas. \(|r^n|=|r|^n\to 0\) car \(0\leqslant |r|\lt 1\), et donc \(s_n\to \frac{1}{1-r}\).
  • \(r= -1\). Dans ce cas, \(s_n=\frac12(1-(-1)^{n+1})\), et donc ne converge pas.
  • \(r\lt -1\). Dans ce cas, \(r^n=(-|r|)^n=(-1)^n|r|^n\), et puisque \(|r|^n\to+\infty\), \(s_n\) n'a pas de limite lorsque \(n\to\infty\).

On peut observer le comportement de la suite \((s_n)_{n\geqslant 0}\) en fonction de \(-1\lt r\lt 1\) sur l'animation suivante. (On peut en particulier voir comme la suite n'est plus monotone pour des valeurs négatives de \(r\))

Dans le cas \(|r|\lt 1\), on écrit souvent le résultat sous la forme \[ \boxed{1+r+r^2+r^3+\dots=\frac{1}{1-r}} \] La somme infinie, dans le côté gauche, s'appelle la série géométrique, et sa somme est la valeur du côté droit, à savoir \(\frac{1}{1-r}\). (On étudiera les séries dans un chapitre ultérieur.)

On peut utiliser la série géométrique pour obtenir des formules utiles pour des sommes infinies de même nature:

Exemple: Fixons un \(|r|\lt 1\), et considérons la somme \[ 1-r+r^2-r^3+r^4-r^5+\cdots\,. \] Remarquons que cette dernière peut se récrire \[ 1+(-r)+(-r)^2+(-r)^3+(-r)^4+(-r)^5+\cdots\,, \] qui n'est autre que la série géométrique de raison \(-r\). Comme \(|-r|=|r|\lt 1\), cette dernière converge et sa somme vaut \[ 1-r+r^2-r^3+r^4-r^5+\cdots =\frac{1}{1-(-r)} =\frac{1}{1+r}\,. \]

Exemple: Fixons un \(|r|\lt 1\), et considérons la somme \[ r+r^2+r^3+r^4+\cdots\,. \] On peut récrire cette dernière ainsi: \[\begin{aligned} r+r^2+r^3+r^4+\cdots\, &=(1+r+r^2+r^3+r^4+\cdots)-1\\ &=\frac{1}{1-r}-1\\ &=\frac{r}{1-r}\,. \end{aligned}\]

Exemple: Partons, à l'étape zéro, d'un triangle équilatéral que l'on suppose d'aire égale à \(A_0=1\):

Puis, à l'étape \(1\), on divise chacun de ses trois côtés en trois parties égales, et on remplace chaque partie du milieu par un triangle équilatéral. L'objet obtenu après cette première itération (mettre \(n=1\) dans l'animation ci-dessus) a un bord constitué de \(12\) segments. Remarquons que l'aire de chacun des trois triangles équilatéraux rajoutés vaut \(\frac{1}{9}\), et donc après une itération l'aire totale vaut \[ A_1=1+3\cdot \frac{1}{9}\,. \] Puis on recommence avec chacun des segments du bord de \(A_1\), que l'on divise en trois parties égales, et dont on remplace la partie du milieu par un triangle équilatéral d'aire \((\frac19)^2\). On obtient ainsi un objet dont l'aire vaut maintenant \[ A_2=1+3\cdot \frac{1}{9}+3\cdot 4\cdot \frac{1}{9^2}\,. \] (Voir aussi l'explication de la vidéo ci-dessus.)

En itérant ce processus à l'infini (diviser à chaque étape les segments du bord en trois parties égales, remplacer celui du milieu par un triangle équilatéral, etc), on obtient un objet limite appelé flocon de von Koch, qui est un objet fractal. (Attention: dans l'animation, ne pas tester des \(n\) trop grand, cela risque de faire du mal à votre browser!)
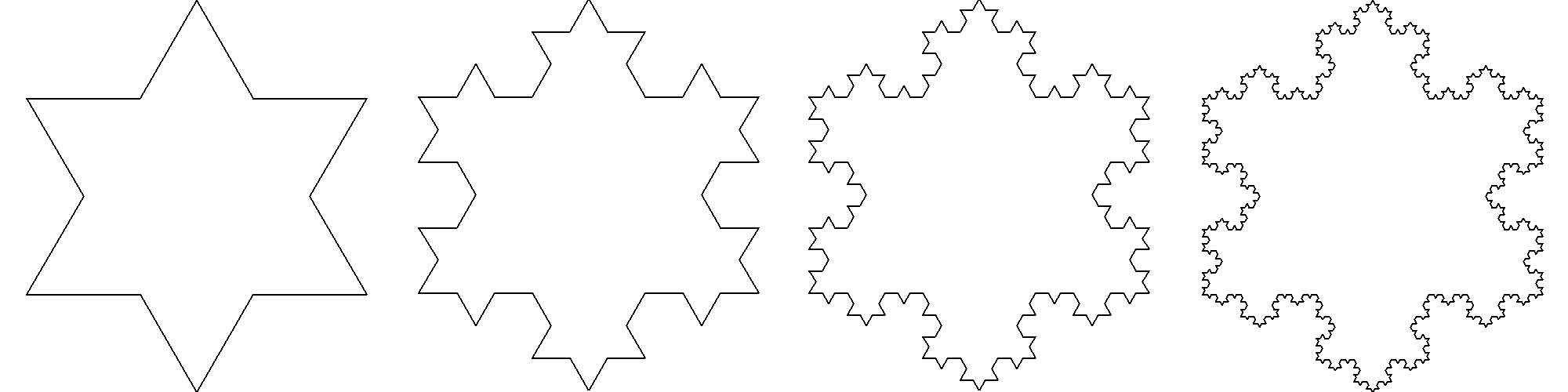
Quelle est l'aire totale du flocon, obtenu après avoir fait \(n\to\infty\)?

Remarquons qu'à chaque étape, le nombre de segments du bord est multiplié par \(4\), et qu'à l'étape \(n\), l'aire de chacun des petits triangles rajoutés vaut \(\frac{1}{9^n}\). On a donc \[\begin{aligned} A_0&=1\\ A_1&=1+3\cdot \frac{1}{9}\\ A_2&=1+3\cdot \frac{1}{9}+3\cdot 4\cdot \frac{1}{9^2}\\ A_3&=1+3\cdot \frac{1}{9}+3\cdot 4\cdot \frac{1}{9^2}+3\cdot 4\cdot 4\cdot \frac{1}{9^3}\\ \vdots&\\ A_n&=1+3\cdot \frac{1}{9}+3\cdot 4\cdot \frac{1}{9^2}+3\cdot 4\cdot 4\cdot \frac{1}{9^3}+\cdots+ 3\cdot 4^{n-1}\cdot \frac{1}{9^n}\,, \end{aligned}\] que l'on peut récrire plus proprement: \[ A_n= 1+\frac13 \Bigl\{ 1+\frac{4}{9}+\frac{4^2}{9^2}+ \frac{4^3}{9^3}+\dots\frac{4^{n-1}}{9^{n-1}} \Bigr\} \] On reconnaît ici une somme géométrique de raison \(r=\frac49\lt 1\), qui dans la limite \(n\to\infty\) devient une série géométrique convergente pour laquelle on peut utiliser notre formule: \[ \lim_{n\to \infty} A_n=1+\frac13\cdot \frac{1}{1-\frac49}=1+\frac13\cdot\frac95=\frac85\,. \]

Application: existence du nombre \(e\)

Dans cette section, on étudie la suite \[ e_n:= \Bigl(1+\frac1n\Bigr)^n\,. \] Dans la limite \(n\to \infty\), \(e_n\) mène à une indétermination de la forme ''\(1^\infty\)'', et il n'est pas clair, a priori, de comment se comporte vraiment \(e_n\).

Donnons deux arguments légitimes, mais tous les deux faux, concernant le comportement de \(e_n\) dans la limite \(n\to \infty\). On va pourtant montrer que le vrai comportement de cette suite ne suit aucun de ces scénarios. On peut déjà s'en convaincre en testant soi-même, avec \(x_n=\)pow(1+1/n,n)...

Théorème: ⚡ Soit \((e_n)_{n\geqslant 1}\) la suite définie ci-dessus. Alors

  1. \((e_n)\) est strictement croissante,
  2. \((e_n)\) est bornée: \(2\leqslant e_n\lt 3\) pour tout \(n\geqslant 1\).
Par conséquent, il existe \(e\in [2,3]\) tel que \[\lim_{n\to \infty} e_n=e\,.\]

Pour commencer, utilisons la formule du binôme de Newton pour écrire \(e_n\) sous une forme qui permette de mieux étudier sa dépendance en \(n\): \[\begin{aligned} e_n= \Bigl(1+\frac1n\Bigr)^n &=1+\sum_{k=1}^n\binom{n}{k}1^{n-k}(\tfrac1n)^k\\ &=1+\sum_{k=1}^n\frac{n!}{k!(n-k)!}(\tfrac1n)^k\\ &=1+\sum_{k=1}^n\frac{1}{k!}\frac{n(n-1)(n-2)\cdots(n-k+1)}{n\cdot n\cdots n}\\ &=1+\sum_{k=1}^n\frac{1}{k!} \bigl(1-\tfrac1n\bigr)\cdots \bigl(1-\tfrac{k-1}{n}\bigr) \end{aligned}\] On utilise deux fois cette expression.

  • Affirmation:\((e_n)\) est croissante. En utilisant l'expression précédente, pour \(n+1\) \[\begin{aligned} e_{n+1} &=1+\sum_{k=1}^{n+1}\frac{1}{k!} \bigl(1-\underbrace{\tfrac1{n+1}}_{\lt \frac1n}\bigr)\cdots \bigl(1-\underbrace{\tfrac{k-1}{n+1}}_{\lt \frac{k-1}{n}}\bigr)\\ &\gt 1+\sum_{k=1}^{n+1}\frac{1}{k!} \bigl(1-\tfrac1{n}\bigr)\cdots \bigl(1-\tfrac{k-1}{n}\bigr)\\ &= 1+\sum_{k=1}^{n}\frac{1}{k!} \bigl(1-\tfrac1{n}\bigr)\cdots \bigl(1-\tfrac{k-1}{n}\bigr)=e_n\,. \end{aligned}\] Dans l'avant-dernière égalité, on a utilisé le fait que si \(k=n+1\), alors \(1-\frac{k-1}{n}=0\). Comme \(e_n\) est strictement croissante, on a en particulier que \(e_n> e_1=2\).
  • Affirmation:\((e_n)\) est majorée par \(M=3\). En utilisant encore une fois l'expression ci-dessus, \[\begin{aligned} e_n &=1+\sum_{k=1}^n\frac{1}{k!} \bigl(\underbrace{1-\tfrac1n}_{\lt 1}\bigr)\cdots \bigl(\underbrace{1-\tfrac{k-1}{n}}_{\lt 1}\bigr)\\ &\lt 1+\sum_{k=1}^n\frac{1}{k!}\\ &=1+\frac{1}{1!}+\sum_{k=2}^n\frac{1}{k!} \end{aligned}\] Remarquons maintenant que pour tout \(k\geqslant 2\), \[ k!= \underbrace{k}_{\geqslant 2}\cdot \underbrace{(k-1)}_{\geqslant 2}\cdots \underbrace{3}_{\geqslant 2}\cdot 2\cdot 1\geqslant 2^{k-1}\,, \] et donc \[ e_n\lt 1+1+\sum_{k=2}^n\frac{1}{2^{k-1}} \lt 1+\sum_{j=0}^\infty\frac{1}{2^{j}}\lt 1+\frac{1}{1-\frac12}=3\,. \]
On a donc montré que \((e_n)\) est croissante et majorée, donc elle converge. Puisque \(2\leqslant e_n\lt 3\) pour tout \(n\), sa limite appartient aussi à cet intervalle.

On connaît aujourd'hui des milliards de chiffres de l'expansion décimale de \(e\). Ses premiers termes sont \[ e= 2.7182818284 5904523536 0287471352 662497\dots \] Euler a montré en \(1737\) que \(e\) est un nombre irrationnel.

Quiz 3.9-1 : Vrai ou faux?
  1. \( 1-1+1-1+1-1+\cdots=\frac{1}{2} \)
  2. \(\displaystyle 1+\frac43+\frac{16}{9}+\frac{64}{27}+\cdots+\frac{65'536}{6'561}= \frac{242'461}{6'561}\)
Quiz 3.9-2 : Vrai ou faux?
  1. Si \(a_n\to 0\), alors \((1+a_n)^n\to 1\)
  2. Si \(a_n\to 0\), alors \((1+a_n)^n\to e\)
  3. Si \(a_n\to \infty\) et \(b_n\to \infty\), alors \((1+\frac{1}{a_n})^{b_n}\to e\)
  4. \[\begin{aligned} \lim_{n\to\infty}(1+\tfrac1n)^n &= \lim_{n\to\infty}\left((1+\tfrac1n) \cdots (1+\tfrac1n)\right)\\ &= \left(\lim_{n\to\infty}(1+\tfrac1n)\right) \cdots \left(\lim_{n\to\infty}(1+\tfrac1n)\right)\\ &=1\cdots 1=1\,. \end{aligned}\]

Dernière compilation: 2024-01-22 (20:49:37)

Sauf indication contraire, le contenu de ce document est soumis à une licence Creative Commons internationale, Attribution: Pas d'Utilisation Commerciale - Partage dans les Mêmes Conditions 4.0 (CC BY-NC-SA 4.0)