Théorème: Soit \((a_n)\) une suite.
- Si \((a_n)\) est croissante et majorée, elle converge.
- Si \((a_n)\) est décroissante et minorée, elle converge.
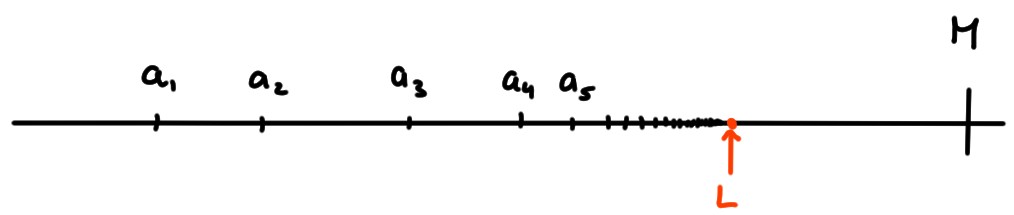
On a vu qu'une suite convergente est forcément bornée. Mais le contraire n'est pas vrai: une suite bornée ne converge pas forcément.
Exemple: La suite \(a_n=(-1)^n\) ne converge pas, mais elle est bornée, puisque \(|a_n|=1\), ce qui implique \(-1\leqslant a_n\leqslant 1\) pour tout \(n\).
Par contre, si une suite est bornée et monotone, alors elle converge:
Théorème: Soit \((a_n)\) une suite.
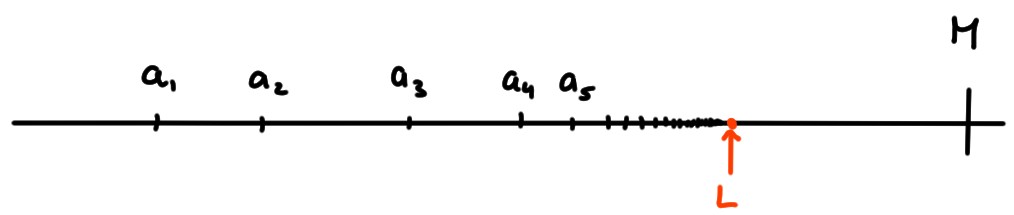
Soit \((a_n)\) une suite croissante et majorée.
Considérons l'ensemble \(A\subset \mathbb{R}\) défini comme étant l'ensemble de tous
les points de la suite:
\[ A:= \{a_1,a_2,a_3,\dots\}\,.
\]
Puisque la suite est bornée, \(A\) est majoré; on peut donc considérer le
réel \(L\) défini par
\[ L:= \sup A\,. \]
Nous allons montrer que \(a_n\to L\).
Par définition, le supremum est un majorant, et donc
\(a_n\leqslant L\) pour tout \(n\).
De plus, comme le supremum est le plus petit majorant, on a que
pour tout \(\varepsilon\gt 0\), il existe \(n_*\) tel que
\(L-\varepsilon\leqslant a_{n_*}\).
Or comme la suite est croissante, on a
\[
L-\varepsilon\leqslant a_{n_*}\leqslant a_{n_*+1}\leqslant a_{n_*+2}\leqslant \cdots \leqslant L\,,
\]
ce qui implique \(|a_n-L|\leqslant \varepsilon\) pour tout \(n\geqslant n_*\).
On a ainsi montré que pour tout \(\varepsilon\gt 0\), on a \(|a_n-L|\leqslant \varepsilon\)
pour tout \(n\) suffisamment grand. Ceci montre que \(a_n\to L\).
(Dans le deuxième cas, lorsque la suite est décroissante et minorée,
on adapte cet argument après avoir défini \(L:= \inf A\).)
Si le résultat peut paraître intuitif, la preuve a montré qu'il repose entièrement sur l'existence d'un supremum pour les ensembles majorés de \(\mathbb{R}\).
Le théorème ci-dessus garantit que si une suite est monotone et bornée, alors elle possède une limite \(L\), qui est soit un supremum (si la suite est croissante et majorée), soit un infimum (si la suite est décroissante et minorée). Parfois, on peut calculer cette limite \(L\) explicitement:
Exemple: Considérons la suite \((a_n)_{n\geqslant 0}\) définie par \[ a_n=\frac{n}{n+1}\,. \] Nous avons montré précédemment que cette suite est strictement croissante. Or elle est aussi majorée, puisque \(n\lt n+1\) implique \[ a_n=\frac{n}{n+1}\lt \frac{n+1}{n+1}=1\,. \] Le théorème ci-dessus garantit donc qu'elle converge, et que sa limite est égale à \[ L=\sup\{a_0,a_1,a_2,\dots\}\,. \] On peut vérifier (exercice!) que \(L=1\).
L'exemple suivant présente un cas dans lequel le théorème permet de montrer qu'une certaine suite converge, mais sans pour autant donner la valeur de la limite.
Exemple: Soit \((b_n)\) la suite définie ainsi: \[\begin{aligned} b_1&:= \frac{1}{1^2}\\ b_2&:= \frac{1}{1^2}+\frac{1}{2^2}\\ b_3&:= \frac{1}{1^2}+\frac{1}{2^2}+\frac{1}{3^2}\\ \vdots&\\ b_n&:= \frac{1}{1^2}+ \frac{1}{2^2}+ \frac{1}{3^2}+ \frac{1}{4^2}+\cdots+ \frac{1}{n^2}\\ b_{n+1}&:= \frac{1}{1^2}+ \frac{1}{2^2}+ \frac{1}{3^2}+ \frac{1}{4^2}+\cdots+ \frac{1}{n^2}+\frac{1}{(n+1)^2}\\ \vdots& \end{aligned}\] Cette suite est croissante puisque \(b_{n+1}=b_n+\frac{1}{(n+1)^2}\gt b_n\). Pour montrer qu'elle est bornée, remarquons que pour tout \(k\geqslant 2\), \[ \frac{1}{k^2}=\frac{1}{k\cdot k}\lt \frac{1}{k(k-1)}=\frac{1}{k-1}-\frac{1}{k}\,. \] En utilisant cette inégalité pour \(k=2,3,\dots,n\), on obtient une borne supérieure dans laquelle beaucoup de termes se téléscopent: \[\begin{aligned} b_n&= \frac{1}{1^2}+ \frac{1}{2^2}+ \frac{1}{3^2}+ \frac{1}{4^2}+\cdots+ \frac{1}{n^2} \\ &\lt\tfrac{1}{1^2}+ \bigl( \tfrac11 \underbrace{- \tfrac12 \bigr) +\bigl( \tfrac12}_{=0} \underbrace{- \tfrac13 \bigr) +\bigl( \tfrac13}_{=0} \underbrace{- \tfrac14 \bigr) +\bigl( \tfrac14}_{=0}- \cdots \underbrace{-\tfrac{1}{n-1} \bigr) +\bigl( \tfrac1{n-1}}_{=0} - \tfrac1n \bigr) \end{aligned}\] On a donc que \[ b_n\lt \frac{1}{1^2}+\frac{1}{1}-\frac1n=2-\frac1n\lt 2\,. \] On a ainsi montré que \((b_n)\) est majorée par \(M=2\), et comme elle est aussi croissante, elle converge: il existe \(L\in\mathbb{R}\) tel que \[ \lim_{n\to \infty} b_n=L\,. \] Puisque \(1\leqslant b_n\lt 2\), on a aussi que \(1\leqslant L\leqslant 2\).
Dernière compilation: 2024-10-05 (22:34:27)
Sauf indication contraire, le contenu de ce document est soumis à une licence Creative Commons internationale, Attribution: Pas d'Utilisation Commerciale - Partage dans les Mêmes Conditions 4.0 (CC BY-NC-SA 4.0)
