3.3 Propriétés de la limite

Le calcul de limites sera grandement facilité par l'utilisation des propriétés générales satisfaites par les suites convergentes, que nous commencerons à décrire maintenant.

La première propriété dit qu'une suite ne peut pas tendre vers deux limites différentes:

Lemme: Si une suite est convergente, alors sa limite est unique.

Supposons, par l'absurde, que \(a_n\to L\) et \(a_n\to L'\), avec \(L\neq L'\). Si on suppose par exemple que \(L\lt L'\), alors on peut toujours prendre un \(\varepsilon\gt 0\) suffisamment petit, de manière à ce que les intervalles \([L-\varepsilon,L+\varepsilon]\) et \([L'-\varepsilon,L'+\varepsilon]\) soient disjoints:

Plus concrètement, on peut garantir que ces intervalles sont disjoints en prenant par exemple \[\varepsilon:= \frac{L'-L}{3}\,.\] Maintenant,
  • Comme \(a_n\to L\), il existe \(N\) tel que \(a_n\in [L-\varepsilon,L+\varepsilon ]\) pour tout \(n\geqslant N\).
  • Comme \(a_n\to L'\), il existe \(N'\) tel que \(a_n\in [L'-\varepsilon,L'+\varepsilon]\) pour tout \(n\geqslant N'\).
Cela implique que pour \(n\geqslant \max\{N,N'\}\), \(a_n\) doit être dans les deux intervalles en même temps, une contradiction puisque ces intervalles sont disjoints.

La deuxième est que les valeurs des termes d'une suite convergente ne peuvent pas devenir trop grands:

Lemme: Si une suite converge, alors elle est bornée.

Soit \((a_n)_{n\geqslant 1}\) une suite convergente. Nommons \(L\) sa limite. La convergence de \(a_n\) vers \(L\) implique en particulier que l'on peut fixer, par exemple, \(\varepsilon:= 1\), et considérer l'entier \(N\) tel que \(a_n\in [L-1,L+1]\) pour tout \(n\geqslant N\):

En particulier on a, pour tout \(n\geqslant N\), que \(L-1\leqslant a_n \leqslant L+1\). Si on définit maintenant \[\begin{aligned} M&:= \max\{a_1,a_2,\dots,a_{N-1},L+1\}\\ m&:= \min\{a_1,a_2,\dots,a_{N-1},L-1\}\,, \end{aligned}\] alors on a bien garanti que \(m\leqslant a_n\leqslant M\) pour tout \(n\geqslant 1\).

Lemme: Si \(a_n\to L\), alors \(|a_n|\to |L|\).

Remarquons que l'inégalité triangulaire permet d'écrire \[ |a_n|=|(a_n-L)+L|\leqslant |a_n-L|+|L|\,, \] ainsi que \[ |L|=|(L-a_n)+a_n|\leqslant |a_n-L|+|a_n|\,, \] En combinant ces inégalités, on obtient \[ -|a_n-L|\leqslant |a_n|-|L|\leqslant |a_n-L|\,, \] qui est équivalente à \[ \bigl||a_n|-|L|\bigr|\leqslant |a_n-L|\,. \] Soit maintenant \(\varepsilon\gt 0\). Puisque \(a_n\to L\), il existe \(N\) tel que \(|a_n-L|\leqslant \varepsilon\) pour tout \(n\geqslant N\). Par l'inégalité ci-dessus, ceci implique aussi que \(||a_n|-|L||\leqslant \varepsilon\) pour tout \(n\geqslant N\).

Finalement, listons quelques propriétés qui sont utilisées constamment dans les calculs de limites.

Lemme: (Opérations sur les limites) Soient \((a_n)\) et \((b_n)\) deux suites convergentes: \(a_n\to L_1\), \(b_n\to L_2\). Alors

  1. Limite de la somme: \[ \lim_{n\to \infty}(a_n+b_n)=\bigl(\lim_{n\to \infty} a_n\bigr)+ \bigl(\lim_{n\to \infty} b_n\bigr) =L_1+L_2\,. \]
  2. Limite du produit: \[ \lim_{n\to \infty}(a_n\cdot b_n)=\bigl(\lim_{n\to \infty} a_n\bigr) \cdot\bigl(\lim_{n\to \infty} b_n\bigr) =L_1L_2\,. \]
  3. Limite du quotient: si \(L_2\neq 0\), alors \[ \lim_{n\to \infty}\frac{a_n}{b_n}= \frac{\displaystyle\lim_{n\to \infty} a_n}{\displaystyle\lim_{n\to \infty} b_n} =\frac{L_1}{L_2}\,. \]
  4. Si \(a_n\leqslant b_n\) pour tout \(n\) suffisamment grand, alors \(L_1\leqslant L_2\).

Remarque: Dans la dernière propriété, les ''\(\leqslant\)'' ne peuvent pas être remplacés par des ''\(\lt\)''. En effet, on peut très bien avoir deux suites convergentes telles que \(a_n\lt b_n\) pour tout \(n\) suffisamment grand, mais telles que \(\lim_{n\to \infty} a_n=\lim_{n\to \infty} b_n\). Comme exemple simple, on peut considérer les suites \(a_n=-\frac1n\) et \(b_n=\frac1n\).

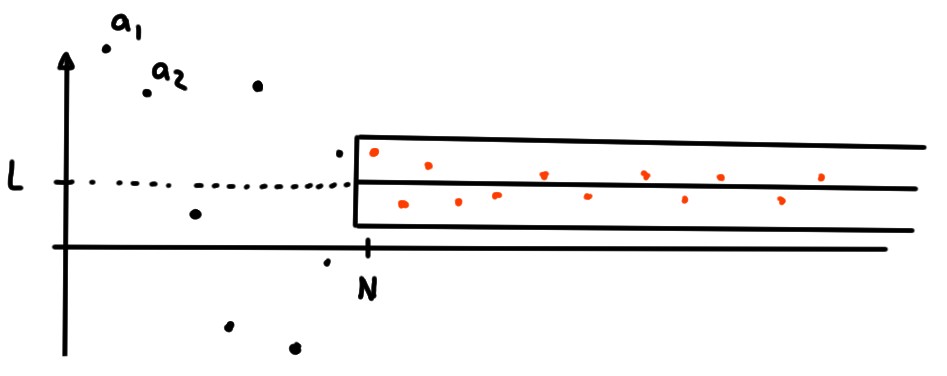
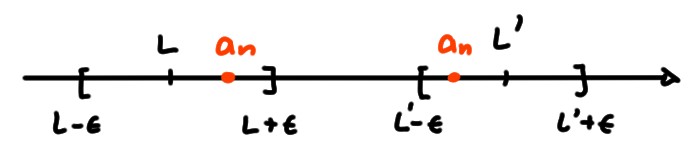1. Par l'inégalité triangulaire, \[\begin{aligned} |(a_n+b_n)-(L_1+L_2)|&=|(a_n-L_1)+(b_n-L_2)|\\ &\leqslant |a_n-L_1|+|b_n-L_2|\,. \end{aligned}\] Fixons un \(\varepsilon\gt 0\), et posons \(\varepsilon':= \varepsilon/2\). Comme \(a_n\to L_1\), il existe \(N_a\) tel que \(|a_n-L_1|\leqslant \varepsilon'\) pour tout \(n\geqslant N_a\). Comme \(b_n\to L_2\), il existe \(N_b\) tel que \(|b_n-L_2|\leqslant \varepsilon'\) pour tout \(n\geqslant N_b\). On a donc, pour tout \(n\geqslant N:= \max\{N_a,N_b\}\), \[ |(a_n+b_n)-(L_1+L_2)|\leqslant |a_n-L_1|+|b_n-L_2|\leqslant 2\varepsilon'=\varepsilon\,. \] 2. Comme \(a_n\) converge, elle est bornée: il existe \(C\gt 0\) telle que \(|a_n|\leqslant C\) pour tout \(n\). On peut donc écrire \[\begin{aligned} |a_nb_n-L_1L_2|&=|a_nb_n-a_nL_2+a_nL_2-L_1L_2|\\ &\leqslant |a_n||b_n-L_2|+|L_2||a_n-L_1|\\ &\leqslant C|b_n-L_2|+|L_2||a_n-L_1|\,. \end{aligned}\] Soit \(\varepsilon\gt 0\). Soit \(N_a\) tel que \(|a_n-L_1|\leqslant \frac{\varepsilon}{2|L_2|}\) pour tout \(n\geqslant N_a\) (serait dommage que \(L_2=0\)!), et soit \(N_b\) tel que \(|b_n-L_2|\leqslant \frac{\varepsilon}{2C}\) pour tout \(n\geqslant N_b\). On a alors que pour tout \(n\geqslant N:= \max\{N_a,N_b\}\), \[\begin{aligned} |a_nb_n-L_1L_2|&\leqslant C|b_n-L_2|+|L_2||a_n-L_1|\\ &\leqslant C\frac{\varepsilon}{2C}+|L_2|\frac{\varepsilon}{2|L_2|}=\varepsilon\,. \end{aligned}\] 3. Il suffit de montrer la propriété dans le cas où \(a_n=1\) pour tout \(n\), c'est-à-dire de montrer que \(b_n\to L_2\neq 0\) implique que \[ \frac{1}{b_n}\to \frac{1}{L_2}\,. \] (En effet, on utilise alors la propriété du produit démontrée plus haut, pour conclure dans le cas général que \(\frac{a_n}{b_n}=a_n\cdot \frac{1}{b_n}\to L_1\cdot\frac{1}{L_2}\).) Pour ce faire, commençons par utiliser le fait que \(b_n\to L_2\) implique \(|b_n|\to |L_2|\gt 0\): donc il existe \(N_0\) tel que \(|b_n|\geqslant |L_2|/2\gt 0\) pour tout \(n\geqslant N_0\). Ensuite, on peut écrire, pour tout \(n\geqslant N_0\), que \[ \left|\frac{1}{b_n}-\frac{1}{L_2}\right| =\frac{|b_n-L_2|}{|L_2|\cdot |b_n|} \leqslant \frac{2}{|L_2|^2}|b_n-L_2|\,. \] Fixons maintenant \(\varepsilon\gt 0\), et posons \(\varepsilon'=\frac{|L_2|^2\varepsilon}{2}\). Comme \(b_n\to L_2\), on sait qu'il existe \(N'\) tel que \(|b_n-L_2|\leqslant \varepsilon'\) pour tout \(n\geqslant N'\). Si on pose \(N=\max\{N_0,N'\}\), on a aussi, pour tout \(n\geqslant N\), \[ \left|\frac{1}{b_n}-\frac{1}{L_2}\right| \leqslant \frac{2}{|L_2|^2}|b_n-L_2| \leqslant \frac{2}{|L_2|^2}\varepsilon'=\varepsilon\,. \] On a donc montré que \(1/b_n\to 1/{L_2}\).
4. La preuve de la dernière propriété est laissée en exercice.

Exemple: Considérons la suite \((x_n)\) définie ainsi: \[ x_n=\frac{6n+4}{8n^3+4n^2} \] La convergence de cette suite peut paraître a priori difficile à étudier, mais remarquons qu'on peut l'écrire comme un produit: \[ x_n=\frac{1}{2} \frac{3n+2}{2n+1} \frac{1}{n^2} =\frac{1}{2}a_nb_n\,, \] où \(a_n=\frac{3n+2}{2n+1}\), \(b_n=\frac{1}{n^2}\). On a montré précédemment que \(a_n\to \frac{3}{2}\), et on montre facilement que \(b_n\to 0\); en effet, si \(\varepsilon\gt 0\), alors \(|b_n|\leqslant \varepsilon\) dès que \(n\geqslant N\), où \(N\) est un entier quelconque plus grand que \(1/\sqrt{\varepsilon}\). On peut maintenant utiliser la propriété ci-dessus pour des limites de produits, et conclure que \[ \lim_{n\to\infty}x_n= \lim_{n\to\infty} \frac12 a_nb_n= \frac12 \bigl(\lim_{n\to\infty}a_n\bigr) \bigl(\lim_{n\to\infty}b_n\bigr)= \frac12\cdot \frac32 \cdot 0=0\,. \] On a donc montré que \(x_n\) converge et que sa limite est égale à zéro. Il est important d'apprécier le fait que si on avait voulu le montrer uniquement à partir de la définition de limite, il faudrait montrer que pour tout \(\varepsilon\gt 0\), il existe un \(N\) tel que \[ \left| \frac{6n+4}{8n^3+4n^2} \right| \leqslant \varepsilon\,,\qquad \forall n\geqslant N\,. \] Partir à la recherche de ce \(N\) est possible, mais représente une tâche considérablement plus compliquée que la simple utilisation de la propriété pour la limite d'un produit.

Quiz 3.3-1 : Vrai ou faux?
  1. Si \(a_n\to L\) et \(a_n\to 2L\), alors \(L=0\).
  2. Si \(a_n+b_n\to L_1+L_2\), alors \(a_n\to L_1\) et \(b_n\to L_2\).
  3. Si \(a_n\to a\), \(b_n\to b\) et \(c_n\to c\), alors \[\begin{aligned} a_n+b_n+c_n&\to a+b+c\,,\\ a_nb_nc_n&\to abc\,. \end{aligned}\]
  4. Si \(a_nb_n\) converge, alors \(a_n\) et \(b_n\) convergent.
  5. Si \(\frac{a_n}{b_n}\to L\), alors \(b_n\) ne tend pas vers zéro.
  6. Si \(a_n\lt b_n\) pour tout \(n\) suffisamment grand, et si \(a_n\to L_1\), \(b_n\to L_2\), alors \(L_1\lt L_2\).
  7. Si \(a_n\leqslant b_n\) pour une infinité d'indices \(n\), et si \(a_n\to L_1\), \(b_n\to L_2\), alors \(L_1\leqslant L_2\).

Dernière compilation: 2023-09-08 (17:31:17)

Sauf indication contraire, le contenu de ce document est soumis à une licence Creative Commons internationale, Attribution: Pas d'Utilisation Commerciale - Partage dans les Mêmes Conditions 4.0 (CC BY-NC-SA 4.0)