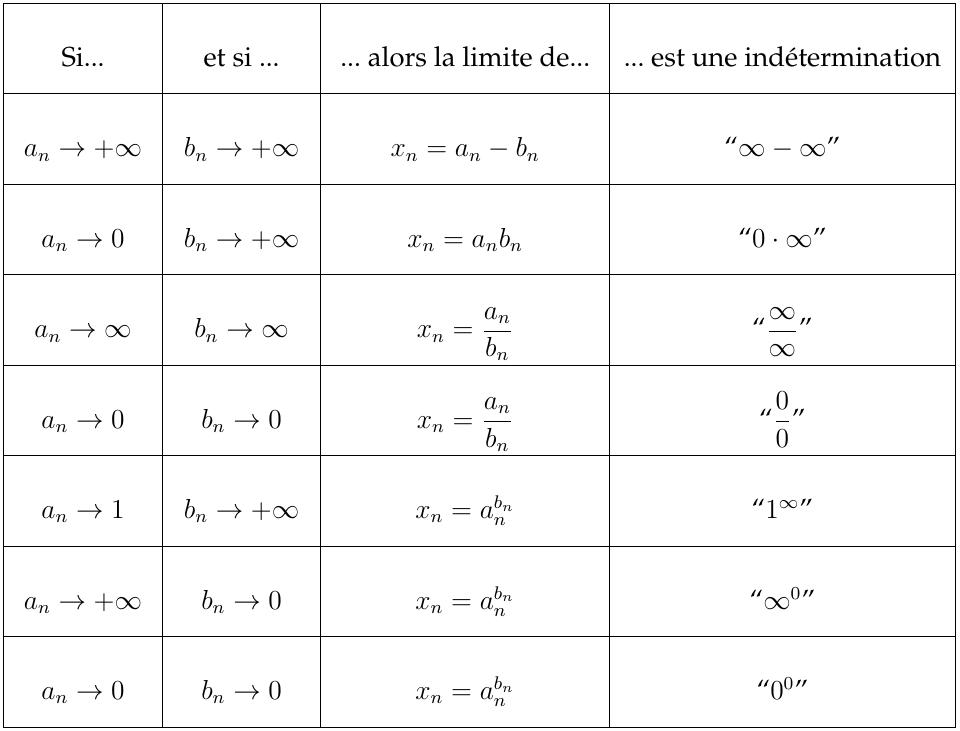
On a pour l'instant considéré deux types de limites:
Or les limites importantes de l'analyse, celles
qui permettent de faire avancer le développement du calcul différentiel
et intégral, sont toutes des limites qui impliquent une forme ou une autre
d'indétermination.
Une limite représente une indétermination
lorsqu'elle fait intervenir une combinaison de
grandeurs qui est telle qu'on
ne peut pas déterminer sa valeur directement à l'aide d'une des
propriétés de base des limites vues précédemment
.
Plus précisément, une indétermination apparaît lorsque une suite est composée d'autres suites,
présentant des comportement du type ''tend vers zéro'' ou ''tend vers
l'infini''.
On décrit les principales indéterminations en considérant une suite \(x_n\)
formée à partir de deux autres suites, que l'on notera \(a_n\) et \(b_n\).
On suppose les comportements
de \(a_n\) et \(b_n\) connus lorsque \(n\to\infty\).
Nous ne traiterons pas les indéterminations de façon générale puisque justement, leur présence indique qu'une étude au cas par cas est nécessaire. Nous allons donc discuter certaines de ces indéterminations, et présenter quelques techniques qui permettent de les résoudre, sur des exemples. Notons que ces techniques ne sont pas spécifiques au cas \(n\to\infty\): toutes seront utiles plus tard, dans d'autres types de limites (comme \(x\to x_0\)).
Exemple:
Nous avons
déjà rencontré
la suite
\[ x_n=\frac{n^2}{n+1}\,,
\]
qui est du type ''\(\frac{\infty}{\infty}\)'' puisque \(n^2\to +\infty\)
et \(n+1\to +\infty\). Nous avions également montré
qu'elle tend vers \(+\infty\), l'intuition derrière ce fait étant
la présence de l'exposant ''\(2\)'' fait que le numérateur l'emporte
dans la limite \(n\to \infty\).
Une autre façon de traiter ce quotient est de l'écrire comme un produit:
\[
\frac{n^2}{n+1}=\underbrace{n}_{=a_n}\cdot \underbrace{\frac{n}{n+1}}_{=b_n}
\]
On a alors \(a_n\to+\infty\) et \(b_n\to 1\), ce qui implique
(par une propriété énoncée et démontrée
ici)
que
\[
\frac{n^2}{n+1}=a_nb_n\to +\infty\,.
\]
Ainsi, en récrivant notre suite, on a pu la mettre sous une forme qui permet de
déduire son comportement à l'aide d'une propriétés de base des suites.
Exemple: Considérons \[\lim_{n\to \infty}\frac{3n^3-17n+1}{5n^3+\sin(n)}\,,\] qui est effectivement une indétermination de la forme ''\(\frac{\infty}{\infty}\)'', puisque
Exemple: Les comparaisons des comportements logarithmiques, polynomiaux et exponentiels, ont consisté à résoudre les indéterminations ''\(\frac{\infty}{\infty}\)'' suivantes: \[ x_n=\frac{\bigl(\log_r (n)\bigr)^\beta}{n^\alpha}\to 0\,,\qquad x_n=\frac{n^\alpha}{r^n}\to 0\,. \] Remarquons que ces limites ont requis une analyse plus fine, puisque numérateur et dénominateur sont de nature différente (on n'a pas pu simplement extraire de ''terme dominant'').
Souvent, une suite est définie par une différence de deux nombres qui deviennent de plus en plus grands à mesure que \(n\) augmente. Or la différence de deux nombres grands peut, a priori, avoir n'importe quel type de comportement.
Exemple: Considérons \[ \lim_{n\to \infty} \bigl(n^3-5n^2\bigr)\,, \] dans laquelle \(a_n=n^3\to +\infty\) et \(b_n=5n^2\to \infty\). Comme \(a_n\) tend vers l'infini plus vite que \(b_n\), dû au fait qu'il contient un terme de degré \(3>2\), on a avantage à mettre \(n^3\) en évidence et obtenir un produit, \[ a_n-b_n=n^3-5n^2=\underbrace{n^3}_{a_n'}\underbrace{\Bigl(1-\frac{5}{n}\Bigr)}_{b_n'} \] Maintenant, on a toujours \(a_n'\to \infty\), mais puisque \(b_n'=1-\frac{5}{n}\to 1\neq 0\), leur produit tend vers \(+\infty\). On a donc \[\lim_{n\to \infty} a_nb_n=\lim_{n\to \infty} a_n'b_n'=+\infty\,.\]
L'identité élémentaire
\[
(a-b)(a+b)=
a^2-b^2
\]
est souvent utile lorsqu'on a affaire à une différence \(a-b\), si on la formule
comme suit:
\[ a-b=\frac{(a-b)(a+b)}{(a+b)}=\frac{1}{a+b}(a^2-b^2) \]
Ici, on a multiplié et divisé par le conjugué de \(a-b\).
Ainsi, à la différence ''\(a-b\)'' se substitue la différence
''\(a^2-b^2\)'', qui est parfois plus facile à traiter.
Cette approche est particulièrement efficace lorsqu'on a des différences de
racines:
Exemple: Considérons \[ \lim_{n\to \infty} \bigl\{\sqrt{n+1}-\sqrt{n}\bigr\}\,, \] qui est bien du type ''\(\infty-\infty\)''. En multipliant et divisant par le conjugué, \[\begin{aligned} \sqrt{n+1}-\sqrt{n}&= \bigl(\sqrt{n+1}-\sqrt{n}\bigr) \frac{\sqrt{n+1}+\sqrt{n}}{\sqrt{n+1}+\sqrt{n}}\\ &=\frac{(n+1)-n}{\sqrt{n+1}+\sqrt{n}}\\ &=\frac{1}{\sqrt{n+1}+\sqrt{n}}\,. \end{aligned}\] Ce quotient n'est plus indéterminé: \[ \lim_{n\to \infty} \bigl\{\sqrt{n+1}-\sqrt{n}\bigr\}= \lim_{n\to \infty} \frac{1}{\sqrt{n+1}+\sqrt{n}}=0\,. \]
Parfois, on pourra (même si c'est assez rare) résoudre une indétermination ''\(\infty-\infty\)'', de la forme \(\lim_{n\to\infty}(a_n-b_n)\), en extrayant explicitement de \(a_n\) et de \(b_n\) la même partie divergente:
Exemple: Considérons le cas ''\(\infty-\infty\)'' suivant: \[ \lim_{n\to\infty}\bigl(\log(e^{\sqrt{n}}+2)-\log(e^{\sqrt{n}}+1)\bigr) \] Ici, on peut remarquer qu'en écrivant \[\begin{aligned} a_n&=\log(e^{\sqrt{n}}+2)=\log(e^{\sqrt{n}}(1+2e^{-{\sqrt{n}}}))={\sqrt{n}}+\log(1+2e^{-{\sqrt{n}}})\,,\\ b_n&=\log(e^{\sqrt{n}}+1)=\log(e^{\sqrt{n}}(1+e^{-{\sqrt{n}}}))={\sqrt{n}}+\log(1+e^{-{\sqrt{n}}})\,, \end{aligned}\] ce qui montre que \(a_n\) et \(b_n\) contiennent tous deux un ''\(\sqrt{n}\)'', qui tend vers l'infini, et qui disparaît lorsqu'on fait la différence: \[\begin{aligned} \lim_{n\to\infty}(a_n-b_n)&= \lim_{n\to \infty}\left( \log(1+2e^{-{\sqrt{n}}}) -\log(1+e^{-{\sqrt{n}}}) \right)\\ &=\log(1)-\log(1)\\ &=0\,. \end{aligned}\] C'est donc un cas d'une indétermination ''\(\infty-\infty\)'' dans laquelle on peut montrer que les infinis se ''compensent exactement''.
Nous reviendrons au indéterminations ''\(\frac00\)'', puisqu'elles sont au coeur
du problème de la dérivation, un outil central de l'analyse.
Pour l'instant, donnons déjà une limite classique ''\(\frac00\)'':
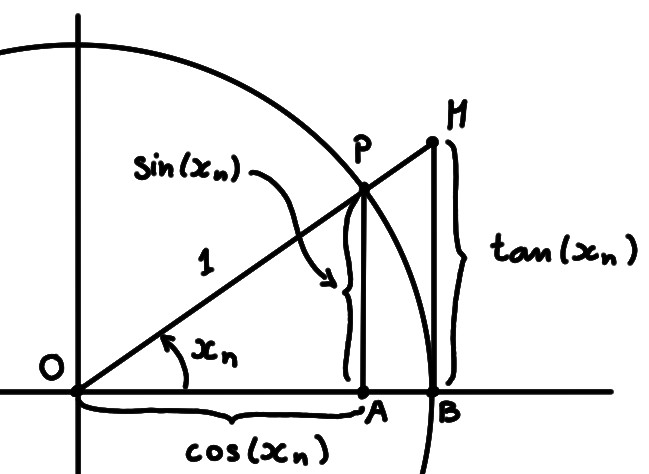
Théorème: Soit \((x_n)\) une suite représentant des mesures d'angles en radians. Si \(x_n\neq 0\) pour tout \(n\), et si \(x_n\to 0\), alors \[ \lim_{n\to \infty}\frac{\sin(x_n)}{x_n}=1\,. \]
Comme la fonction \(x\mapsto \frac{\sin(x)}{x}\) est paire, on peut supposer que
\(x_n\gt 0\) pour tout \(n\).
Puisque \(x_n\to 0\), on a \(0\lt x_n\lt \frac{\pi}{2}\) pour tout \(n\)
suffisamment grand.
Considérons donc un angle sur le cercle trigonométrique, dont la mesure en
radians \(x_n\) est entre \(0\) et \(\tfrac{\pi}{2}\):
Toutes les indéterminations du tableau présenté plus haut sont équivalentes, dans le sens où on peut toujours transformer une indétermination en une autre. Voyons les principaux cas.