La façon la plus simple est de la représenter simplement comme un ensemble de points sur la droite, \(\{a_1,a_2,\dots\}\subset \mathbb{R}\):
Dans un cours comme celui-ci, le chapitre sur les suites représente le premier dans lequel on rencontre pour la première fois quelques-unes de difficultés centrales de l'analyse. En particulier, on y discutera pour la première fois de la notion de limite.
La suite peut commencer par un indice \(n_0\) quelconque, mais le plus souvent on considérera \(n_0=0\) ou \(n_0=1\). Quand le premier indice n'importe pas ou peu (ce qui sera le cas lorsqu'on étudiera le comportement de \(a_n\) pour des indices \(n\) grands), on écrira parfois \((a_n)\) au lieu de \((a_n)_{n\geqslant n_0}\).
On se représente en général une suite \((a_n)_{n\geqslant 1}\) de deux façons.
La façon la plus simple est de la représenter simplement comme un ensemble de points sur la droite, \(\{a_1,a_2,\dots\}\subset \mathbb{R}\):
Du fait que cet ensemble est ordonné, cette image peut aussi s'interpréter comme une trajectoire: une particule est au point \(a_1\) au temps \(n=1\), puis au point \(a_2\) au temps \(n=2\), etc.
Mais une façon plus intuitive de se représenter une suite est de la voir comme le graphe d'une fonction \[\begin{aligned} f:\mathbb{N}^*&\to\mathbb{R}\\ n&\mapsto f(n):= a_n\,. \end{aligned}\] Ceci revient à représenter les paires de points \((n,f(n))=(n,a_n)\) dans le plan cartésien:
Souvent, une suite est définie simplement en disant comment le \(n\)-ème terme \(a_n\) se calcule explicitement en fonction de l'indice \(n\). Lorsqu'une suite est définie ainsi, chaque terme peut être calculé directement, indépendamment des autres, à l'aide d'une formule.
Exemple: Soit \((a_n)_{n\geqslant 1}\) la suite définie ainsi: pour chaque \(n\geqslant 1\), \[ a_n=\frac{3n^3+n-5}{5n^2+7}\,. \] Dans cet exemple, \(a_{10'000}\) peut se calculer directement, sans avoir forcément besoin de calculer les autres.
Exemple: Soit \((a_n)_{n\geqslant 0}\), définie ainsi: \(a_0=\frac{1}{3}\), puis pour tout \(n\geqslant 1\), \[ a_n=4a_{n-1}(1-a_{n-1})\,. \] Cette suite est définie par récurrence: à part le premier, chaque terme est défini en fonction du précédent. Donc on ne peut calculer \(a_{10'000}\) que si on a déjà calculé \(a_{9'999}\), \(a_{9'998}\), etc. Ce type de suite sera étudié dans un chapitre à part.
On peut définir une suite de façon tout à fait arbitraire, ce qui mène rapidement à des suites difficiles à étudier:
Exemple: Considérons l'expansion décimale du nombre \(\pi\), \[ \pi=3.1415926535897932384626433\dots, \] et définissons la suite \((a_n)_{n\geqslant 1}\), comme suit: \[ a_1=1\,,\quad a_2=4\,,\quad a_3=1\,,\quad a_4=5\,,\quad a_5=9\,,\quad a_6=2\,,\quad\dots \] Plus précisément: \(a_n\) est l'entier représentant le \(n\)-ème chiffre après la virgule dans l'expansion décimale de \(\pi\). Une suite facile à définir, mais très difficile à étudier...
Une propriété simplificatrice, pour une suite, est que ses termes ne soient globalement pas trop grands:
Exemple: Considérons la suite \[a_n=1-n^2\,,\qquad n\geqslant 0\,. \] Alors \((a_n)_{n\geqslant 0}\) est majorée. En effet, \(n^2\geqslant 0\) pour tout \(n\), et donc \[a_n=1-n^2\leqslant 1\,,\qquad \forall n\geqslant 0\,.\] et donc en prenant \(M=1\), on a \(a_n\leqslant M\) pour tout \(n\).
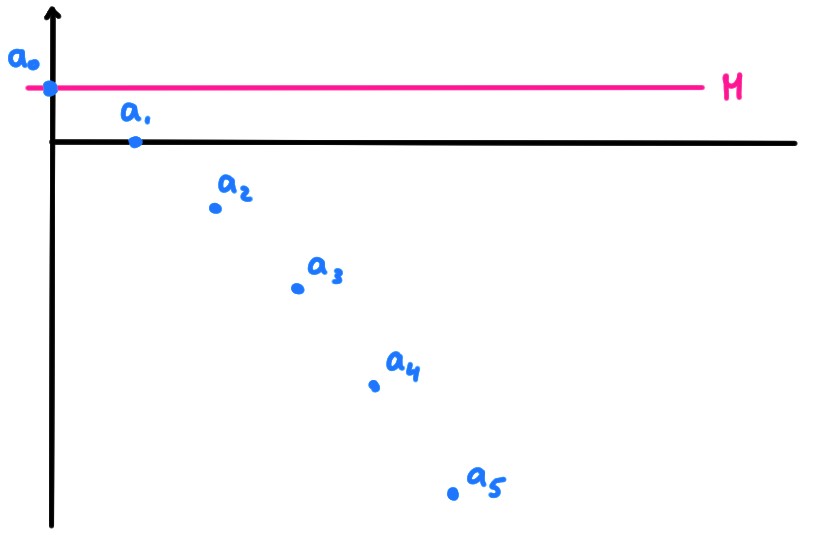
Par contre, \(a_n\) n'est pas minorée (et donc pas bornée). En effet, montrons que pour toute constante \(m\), il existe un indice \(n\) tel que \(a_n\lt m\). Ceci est vrai lorsque \(m\geqslant 0\) puisque \(a_n\leqslant 0\) dès que \(n\geqslant 1\). Si maintenant \(m\lt 0\), alors \(a_n=1-n^2\lt m\) si et seulement si \(n\gt\sqrt{1-m}\) (on a simplement résolu l'inéquation). Donc en prenant n'importe quel entier \(n\) plus grand que \(\sqrt{1-m}\), on a bien que \(a_n\lt m\). Ceci montre qu'il n'existe aucun minorant pour cette suite.
Exemple:
Considérons la suite \[a_n=2\sin(5n+1)-3\cos(\sqrt{n})\,,\qquad n\geqslant 0\,.\] Puisque \[\begin{aligned} |a_n| &=\big|2\sin(5n+1)-3\cos(\sqrt{n})\big|\\ &\leqslant|2\sin(5n+1)|+|-3\cos(\sqrt{n})|\\ &= 2|\sin(5n+1)|+3|\cos(\sqrt{n})|\\ &\leqslant 2+3=5\,, \end{aligned}\] la suite est bornée: \[ -5\leqslant a_n\leqslant +5\,,\qquad \forall n\,. \]
Exemple: La suite \((a_n)_{n\geqslant 1}\), où \(a_n:= n\)ème chiffre de l'expansion décimale de \(\pi\) en base \(10\), est bornée, car minorée par \(0\), et majorée par \(9\).
Exemple: La suite \(a_n=(-1)^nn\) n'est pas majorée. En effet, fixons un seuil \(M\gt 0\) (sous-entendu: aussi grand que l'on veut), et prenons un entier pair \(n=2k\) quelconque, tel que \(k\gt M/2\). On a alors \[ a_n=a_{2k}=(-1)^{2k}2k=2k\gt M\,.\] Cette suite n'est pas minorée non plus. En effet, fixons un seuil \(m<0\) (sous-entendu: aussi grand que l'on veut, négatif), et prenons un entier impair \(n=2k+1\) quelconque, tel que \(k\gt -(m-1)/2\). On a alors \[ a_n=a_{2k+1}=(-1)^{2k+1}(2k+1)=-(2k+1)\lt m\,.\]
Exemple: La suite \(a_n=n^2\), \(n\geqslant 0\), est strictement croissante puisque \[ a_{n+1}=(n+1)^2=n^2+\underbrace{2n+1}_{\gt 0}\gt n^2=a_n\,. \]
Exemple: La suite harmonique \(a_n=\frac{1}{n}\), \(n\geqslant 1\), est strictement décroissante puisque \[ a_{n+1}=\frac{1}{n+1}\lt \frac1n=a_n \]
Dernière compilation: 2024-10-05 (22:34:27)
Sauf indication contraire, le contenu de ce document est soumis à une licence Creative Commons internationale, Attribution: Pas d'Utilisation Commerciale - Partage dans les Mêmes Conditions 4.0 (CC BY-NC-SA 4.0)
