Une suite est définie par récurrence lorsque chacun de ses termes est défini en fonction du précédent. Plus précisément:
On peut voir une telle suite comme un système dynamique, où \(x_n\) est la position d'une particule sur la droite au temps \(n\); à chaque instant la particule détermine sa prochaine position en fonction de l'actuelle. La suite \(x_0,x_1,x_2,\dots\) est alors la trajectoire de la particule.
À l'inverse de la plupart des exemples de suites rencontrés jusqu'ici,
pour lesquels le \(n\)-ème terme de la suite était défini
explicitement comme fonction de l'entier \(n\) (comme
''\(x_n=\frac{n}{n+1}\)''), l'étude
des suites définies par récurrence est en général bien plus
difficile (on ne peut pas facilement extraire des ''termes dominants'', etc.).
À titre de curiosité, mentionnons deux exemples célèbres.
Exemple:
Un exemple fameux est celui de la
suite logistique,
associée à la fonction \(g(x)=rx(1-x)\), où \(r\gt 0\) est un paramètre fixé:
\[
x_{n+1}=rx_n(1-x_n)
\]
Ici, \(x_n\) modélise la taille d'une population à sa \(n\)-ème génération.
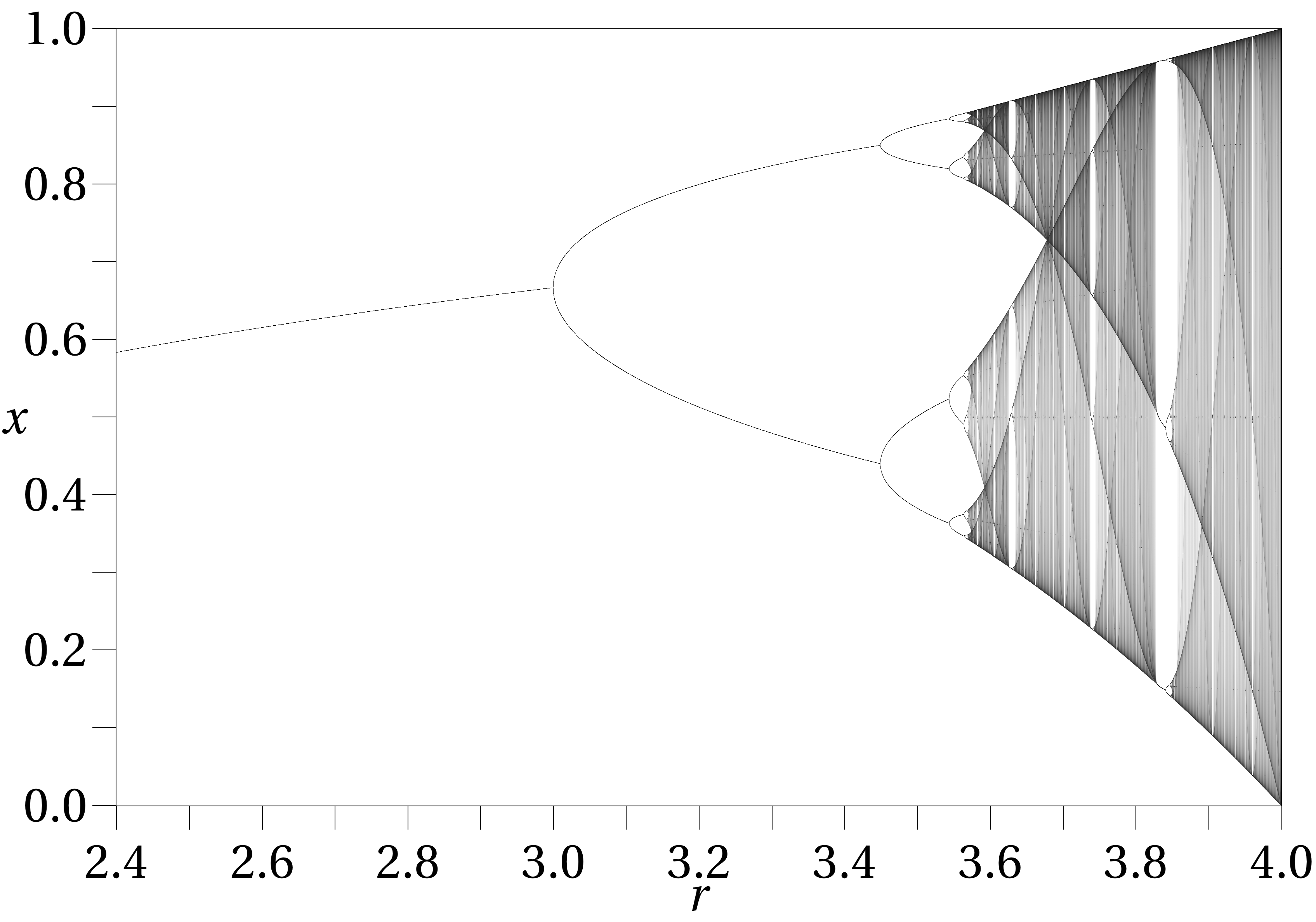
Le comportement de cette suite, dans la limite \(n\to\infty\), dépend fortement
de la valeur du paramètre \(r\). Pour des petites valeurs de \(r\), on peut
montrer (voir exercices) que \(x_n\to 0\), quelle que soit la condition initiale \(x_0\in
[0,1]\). Par contre,
pour des grandes valeurs de \(r\), le comportement de
\(x_n\) devient plus compliqué.
Pour des valeurs \(r\gt 3.8\), le comportement de la suite devient
chaotique.
(Voir l'animation à la fin du chapitre.)
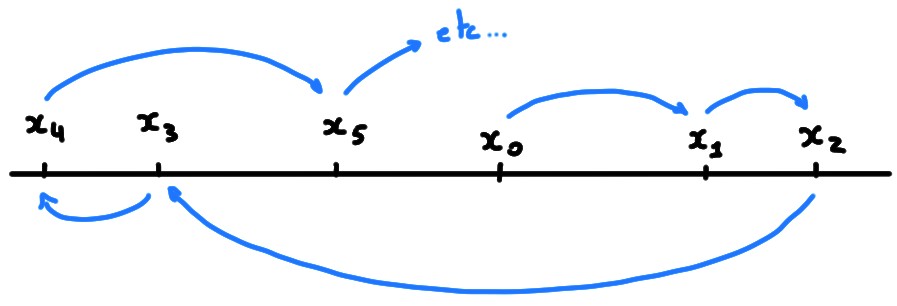
Exemple:
Soit \(g:\mathbb{N}\to\mathbb{N}\) définie par
\[ g(x):=
\begin{cases}
\frac{x}{2}&\text{ si x est pair},\\
3x+1&\text{ si x impair.}
\end{cases}
\]
En choisissant une condition initiale \(x_0\in \mathbb{N}\), la suite
\((x_n)_{n\geqslant 0}\) est une suite de nombres entiers, et
est construite en commençant avec \(x_0\), puis en
définissant
\[
x_{n+1}:= g(x_n)\,.
\]
La compréhension du comportement de cette suite dans la limite \(n\to\infty\)
est un des grands problèmes ouverts ''fameux'' des mathématiques.
On remarque, en essayant plusieurs conditions initiales, que la suite termine
sur la boucle ''\(4,2,1\)''.
Par exemple, en prenant \(x_0=3\), la suite est
\[ 3,10,5,16,8,4,2,1,4,2,1,4,2,1,\dots
\]
En prenant \(x_0=12\),
\[
12, 6, 3, 10, 5, 16, 8, 4, 2, 1,4,2,1,\dots
\]
La Conjecture de Collatz affirme que
la suite termine toujours par la boucle ''\(4,2,1\)'', quelle que soit la
condition initiale. Voir
Veritasium: The simplest math problem no one can solve
Il n'existe pas de ''théorie générale'' permettant de comprendre le comportement asymptotique de toutes les suites définies par récurrence, donc nous nous contenterons de considérer quelques exemples, et de présenter quelques techniques qui permettent de les étudier.
Dernière compilation: 2024-01-22 (20:49:37)
Sauf indication contraire, le contenu de ce document est soumis à une licence Creative Commons internationale, Attribution: Pas d'Utilisation Commerciale - Partage dans les Mêmes Conditions 4.0 (CC BY-NC-SA 4.0)
