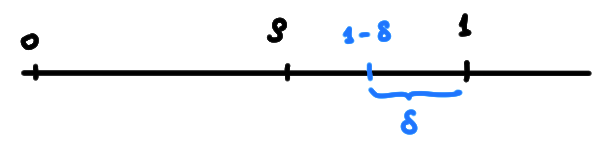
Supposons pour commencer que \(0\leqslant \rho \lt 1\). On peut donc choisir un \(\delta\gt 0\) tel que \(\rho\lt 1-\delta\),
Supposons maintenant que \(\rho\gt 1\), et fixons un \(\delta\gt 0\) tel que \(\rho\gt 1+\delta\). On a alors l'existence d'un entier \(N\) tel que \[ \Bigl|\frac{a_{n+1}}{a_n}\Bigr|\geqslant 1+\delta\qquad \forall n\geqslant N\,. \] En utilisant cette inégalité pour \(N\), \[ |a_{N+1}|\geqslant (1+\delta)|a_N|\,,\] en l'utilisant pour \(N+1\), \[ |a_{N+2}|\geqslant (1+\delta)|a_{N+1}|\geqslant (1+\delta)^2|a_N|\,, \] et ainsi de suite, en l'utilisant pour \(N+k\), \[ |a_{N+k}|\geqslant (1+\delta)|a_{N+(k-1)}|\geqslant\cdots\geqslant (1+\delta)^k|a_N|\,, \] ce qui implique, puisque \((1+\delta)^k\to +\infty\) lorsque \(k\to\infty\), que \[ \lim_{n\to\infty}|a_n|=\lim_{k\to\infty}|a_{N+k}|=+\infty\,. \] Ainsi, \((a_n)\) n'a pas de limite, et si \(a_n\geqslant 0\) pour tout \(n\) suffisamment grand, alors \[ \lim_{n\to\infty}a_n=\lim_{n\to\infty}|a_n|=+\infty\,. \]
