Analyse 1 | S. Friedli (EPFL)

3.12 Le Théorème de Bolzano-Weierstrass

Supposons qu'à l'aide d'un stylo bleu, on place une infinité de points, un à un, dans un intervalle \([a,b]\):

Le Théorème de Bolzano-Weierstrass affirme que peu importe comment on choisit ces points, il existe forcément un point de l'intervalle proche duquel vont s'accumuler une infinité de points bleus.

Le Théorème de Bolzano-Weierstrass

Pour énoncer le théorème rigoureusement, il nous faut un peu de terminologie:

Soit \((x_n)_{n\geqslant 0}\) une suite, et \(0\leqslant n_0\lt n_1\lt n_2\lt \dots\) une suite d'entiers, strictement croissante. Si on pose \[ b_k:= x_{n_k}\,, \] la suite \((b_k)_{k\geqslant 0}=(x_{n_k})_{k\geqslant 0}\) est appelée sous-suite de \((x_n)_{n\geqslant 0}\).

Une sous-suite s'obtient donc à partir de \((x_n)_{n\geqslant 0}\) en ne gardant que certains termes, et en ignorant tous ceux dont l'indice est entre deux entiers consécutifs de la suite \((n_k)_{k\geqslant 0}\):

En choisissant les entiers \(n_k\) et en considérant \((x_{n_k})_k\), on dit qu'on a extrait une sous-suite de \((x_{n})_n\).

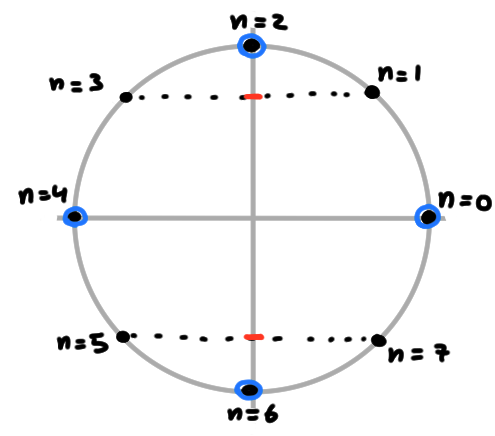
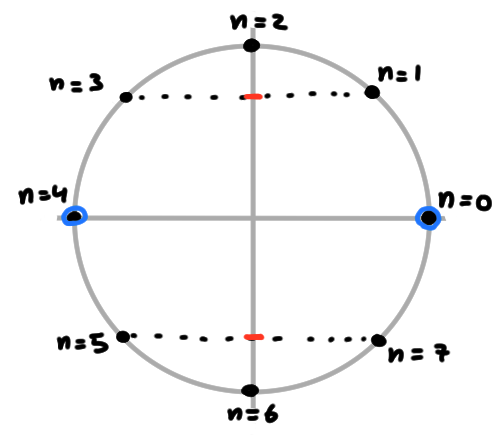
Exemple: Considérons la suite \((x_n)_{n\geqslant 0}\) définie par \[ x_n=\sin(n\tfrac{\pi}{4})\,. \] On comprend cette suite en plaçant l'angle \(n\frac{\pi}{4}\) sur le cercle trigonométrique et en regardant son sinus évoluer sur l'axe \(Oy\). Ses premiers termes, en partant de \(n=0\), sont \[ 0,\frac{\sqrt{2}}{2},1,\frac{\sqrt{2}}{2},0,-\frac{\sqrt{2}}{2},-1, -\frac{\sqrt{2}}{2},0\,. \]

Si on considère les indices pairs, à savoir \(n_k=2k\),
alors \((x_{n_k})_{k\geqslant 0}\) est la suite \(0,1,0,-1,0,1,0,-1,\dots\)
Si on considère les entiers multiples de \(4\), \(n_k=4k\),
alors \((x_{n_k})_{k\geqslant 0}\) est une suite constante puisque \(x_{n_k}=x_{4k}=\sin(k\pi)=0\) pour tout \(k\).

Ces deux exemples ont proposé des sous-suites le long desquelles on observait une certaine régularité, mais on peut considérer des sous-suites arbitraires, par exemple celle obtenue en prenant \(n_k=k^2+[\sqrt{k}]\), pour lesquelles on n'observe en général aucune régularité particulière.

Théorème:(Théorème de Bolzano-Weierstrass) De toute suite bornée \((x_n)_n\) on peut extraire une sous-suite convergente. Plus précisément: Si \(x_n\in [a,b]\) pour tout \(n\), alors il existe \(L\in [a,b]\) et une sous-suite \((x_{n_k})_k\) telle que \(x_{n_k}\to L\).

Soit \(L:= \limsup_{n\to \infty}x_n\), c'est-à-dire \[L=\lim_{n\to \infty} M_n\,,\] où \(M_n=\sup\{x_n,x_{n+1},\dots\}\). Considérons une suite \((\varepsilon_j)_{j\geqslant 1}\) positive, tendant vers zéro. (Pour fixer les idées, on peut choisir \(\varepsilon_j:= \frac{1}{j}\).)

\(j=1\): Par définition de la limite, il existe \(n_1'\) tel que \[ L-\tfrac{\varepsilon_1}{2}\leqslant M_{n_1'}\leqslant L+\tfrac{\varepsilon_1}{2}\,.\] Par définition du supremum, il existe \(n_1\geqslant n_1'\) tel que \[ L-\varepsilon_1\leqslant x_{n_1}\leqslant L+\varepsilon_1\,.\]
\(j=2\): Par définition de la limite, il existe \(n_2'\gt n_1\) tel que \[ L-\tfrac{\varepsilon_2}{2}\leqslant M_{n_2'}\leqslant L+\tfrac{\varepsilon_2}{2}\,.\] Par définition du supremum, il existe \(n_2\geqslant n_2'\) tel que \[ L-\varepsilon_2\leqslant x_{n_2}\leqslant L+\varepsilon_2\,.\]
etc.

Ainsi, on a construit une suite \((n_k)\) strictement croissante telle que pour tout \(k\), \[ L-\varepsilon_k\leqslant x_{n_k}\leqslant L+\varepsilon_k\,. \] Ceci signifie bien que \(x_{n_k}\to L\).

Exemple: Considérons la suite \((x_n)_{n\geqslant 0}\) définie par \[x_n=\cos(e^{3n}+e^{n^2}\sin(5n^3))\,.\] Puisque \(x_n|\in [-1,1]\) pour tout \(n\), le théorème garantit l'existence d'un réel \(L\in [-1,1]\) et d'une sous suite \((x_{n_k})_k\) telle que \(x_{n_k}\to L\) lorsque \(k\to \infty\).

Voyons un exemple simple dans lequel la sous-suite peut être donnée explicitement.

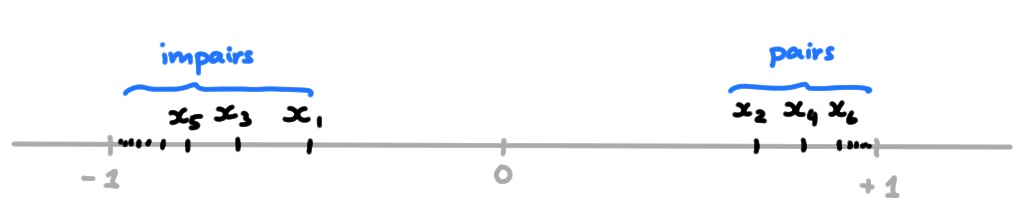
Exemple: Considérons la suite \((x_n)_{n\geqslant 0}\) définie par \[x_n=(-1)^n\frac{n}{n+1}\,,\] qui est bornée puisque \(|x_n|=\frac{n}{n+1}\leqslant 1\). Cette suite ne converge pas, mais le théorème garantit l'existence d'une sous-suite convergente. Ici, on peut extraire explicitement deux sous-suites convergentes, assez naturellement:

Si on ne regarde que les indices pairs, c'est-à-dire que l'on considère \(n_k=2k\), alors on obtient la sous-suite \[x_{2k}=\frac{2k}{2k+1}\,,\] qui converge vers \(1\) lorsque \(k\to\infty\).
Si on ne regarde que les indices impairs, c'est-à-dire que l'on considère \(n_k=2k+1\), alors on obtient la sous-suite \[x_{2k+1}=-\frac{2k+1}{2k+2}\,,\] qui converge vers \(-1\) lorsque \(k\to \infty\).

Donc dans cet exemple, on peut extraire de la suite deux sous-suites différentes, qui ont des limites différentes:

Pour finir, remarquons qu'en général, la conclusion du théorème n'est plus vraie si la suite n'est pas bornée:

Exemple: La suite \(x_n=n\) n'est pas bornée, et elle ne possède aucune sous-suite convergente.

Quiz 3.12-1 : Vrai ou faux?

Si une suite est bornée, alors elle converge.
Si une suite n'est pas bornée, alors elle diverge.
Si toutes les sous-suites d'une suite sont bornées, alors cette suite est bornée.
Si une suite possède une sous-suite bornée, alors elle est bornée.
Si une suite est minorée, alors elle possède une sous-suite convergente.
Toute suite possède une sous-suite convergente.
Si une suite possède une sous-suite convergente, alors elle est bornée.
Si \((a_n)\) est bornée, alors au moins une des suites \((a_{2k})_k\), \((a_{2k+1})_k\), est convergente.
Si une suite \(a_n\) est bornée, alors il existe un unique réel \(L\) et une unique sous-suite \(a_{n_k}\) telle que \(a_{n_k}\to L\).
⚡ Il existe une suite \(a_n\in [0,1]\) possédant la propriété suivante: pour tout \(L\in [0,1]\), il existe une sous-suite \((a_{n_k})_k\) telle que \(a_{n_k}\to L\) lorsque \(k\to\infty\).