Analyse 1 | S. Friedli (EPFL)

5.8 Séries absolument convergentes

Si \(\displaystyle\sum_n|a_n|\) converge, on dit que \(\displaystyle\sum_na_n\) est absolument convergente.

Exemple: La série \[\sum_{n\geqslant 1}\frac{(-1)^n}{n^2}\] est convergente (car c'est une série alternée satisfaisant au critère de Leibniz), mais elle est aussi absolument convergente, car \[\sum_{n\geqslant 1}\left|\frac{(-1)^n}{n^2}\right|=\sum_{n\geqslant 1}\frac{1}{n^2}\,,\] qui est convergente (\(p=2\gt 1\)). Donc l'alternance de signes, dans la série de départ, n'est pas essentielle pour garantir sa convergence.

Exemple: La série harmonique alternée est convergente, comme on sait, mais elle n'est pas absolument convergente, car en prenant la valeur absolue de chacun de ses termes on obtient \[\sum_{n\geqslant 1}\left|\frac{(-1)^{n+1}}{n}\right| =\sum_{n\geqslant 1}\frac{1}{n}\,,\] la série harmonique, qui est divergente. Donc la série harmonique alternée a ''besoin'' de l'alternance de ses signes pour pouvoir converger.

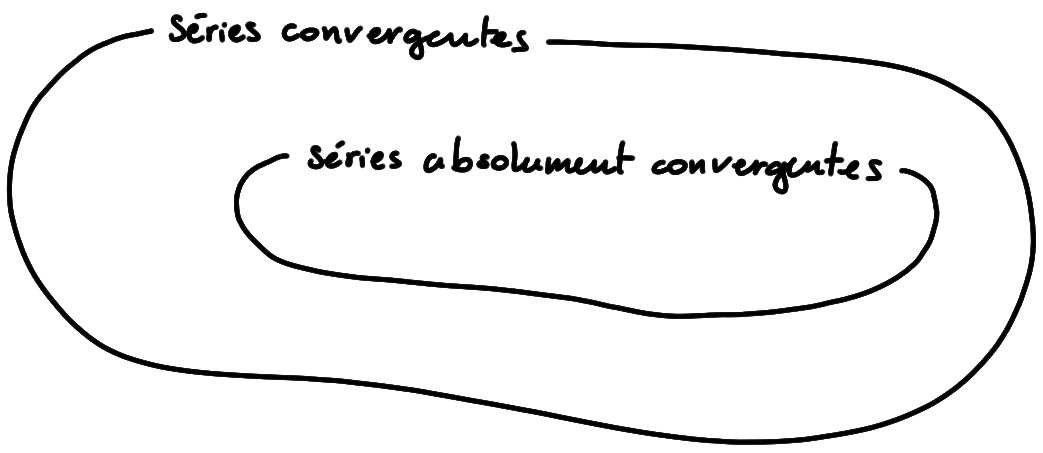
Ce dernier exemple montre qu'une série peut être convergente sans être absolument convergente. D'autre part, on a le résultat important suivant, qui montre que la notion de convergence absolue est plus forte que celle de convergence:

Théorème: Si \(\displaystyle\sum_na_n\) converge absolument, alors elle converge.

Donc l'ensemble des séries absolument convergentes forme un sous-ensemble de l'ensemble des séries convergentes:

Preuve:

Définissons \[\begin{aligned} s_n&:= a_1+\dots+a_n\\ \overline{s}_n&:=|a_1|+\dots+|a_n|\,. \end{aligned}\] Comme \(\sum_na_n\) est absolument convergente, la suite \(\overline{s}_n\) converge, ce qui implique que c'est aussi une suite de Cauchy. Or pour tout \(n\geqslant m\), par l'inégalité triangulaire, \[\begin{aligned} |s_n-s_m|&=\bigl|a_{m+1}+\dots+a_n\bigr|\\ &\leqslant |a_{m+1}|+\cdots +|a_n|\\ &=\overline{s}_n-\overline{s}_m\\ &=|\overline{s}_n-\overline{s}_m|\,. \end{aligned}\] Fixons \(\varepsilon\gt 0\). Comme \((\overline{s}_n)\) est une suite de Cauchy, il existe \(N\) tel que \(|\overline{s}_n-\overline{s}_m|\leqslant\varepsilon\) pour tout \(n,m\geqslant N\). Par l'inégalité ci-dessus, ceci implique que \(|s_n-s_m|\leqslant \varepsilon\) pour tout \(m,n\geqslant N\). On a donc montré que \((s_n)\) est une suite de Cauchy, et donc elle converge: \(\sum_na_n\) est convergente.

Ce résultat peut parfois être utile pour l'étude d'une série:

Exemple: Étudions la convergence de la série \[\sum_{n\geqslant 0} \frac{3\sin(n)-5\cos(n^2)}{2^n+\sqrt{n}}\,. \] Le numérateur contient des parties oscillantes qui compliquent l'étude de la convergence. Pourtant, \[ |3\sin(n)-5\cos(n^2)|\leqslant 3+5=8\,, \] et donc \[ 0\leqslant |a_n|= \Bigl|\frac{3\sin(n)-5\cos(n^2)}{2^n+\sqrt{n}} \Bigr| \leqslant \frac{8}{2^n}=:b_n\,. \] Comme \(\sum_nb_n=8\sum_n\frac{1}{2^n}\) converge (géométrique de raison \(r=\frac12\)), le critère de comparaison implique que \(\sum_n|a_n|\) converge. Donc \(\sum_na_n\) converge absolument, et par le théorème ci-dessus, ceci implique que \(\sum_na_n\) converge.

Dans les deux prochaines sections, nous verrons deux critères très utiles qui garantissent la convergence absolue (et donc la convergence) d'une série.

Quiz 5.8-1 : Vrai ou faux?

Soit \((s_n)\) la suite des sommes partielles d'une série \(\sum_na_n\). Si \(|s_n|\) converge, alors \(\sum_{n\geqslant 0}a_n\) converge absolument.
Soit \(\overline{s}_n:= |a_0|+|a_1|+\cdots +|a_n|\). Si \((\overline{s}_n)\) est majorée, alors \(\sum_{n\geqslant 0}a_n\) converge absolument.
Si \(\sum_na_n\) converge absolument, alors \(a_n\geqslant 0\) pour tout \(n\) suffisamment grand.
Si \(\sum_na_n\) converge absolument, et si \(\sum_n|a_n|=|L|\), alors \(\sum_na_n=\pm L\).
Si \(\sum_na_n\) ne converge pas absolument, alors \(|a_n|\) ne tend pas vers zéro.
Si \(\sum_na_n\) diverge, alors \(\sum_n|a_n|\) diverge.
Si \(\sum_{n\geqslant 0}a_n\) converge, que sa somme vaut \(s>0\), alors \(\sum_{n\geqslant 0}a_n\) converge absolument.
Si \(\sum_na_n\) converge, et si \(b_n\to 0\), alors \(\sum_na_nb_n\) converge.