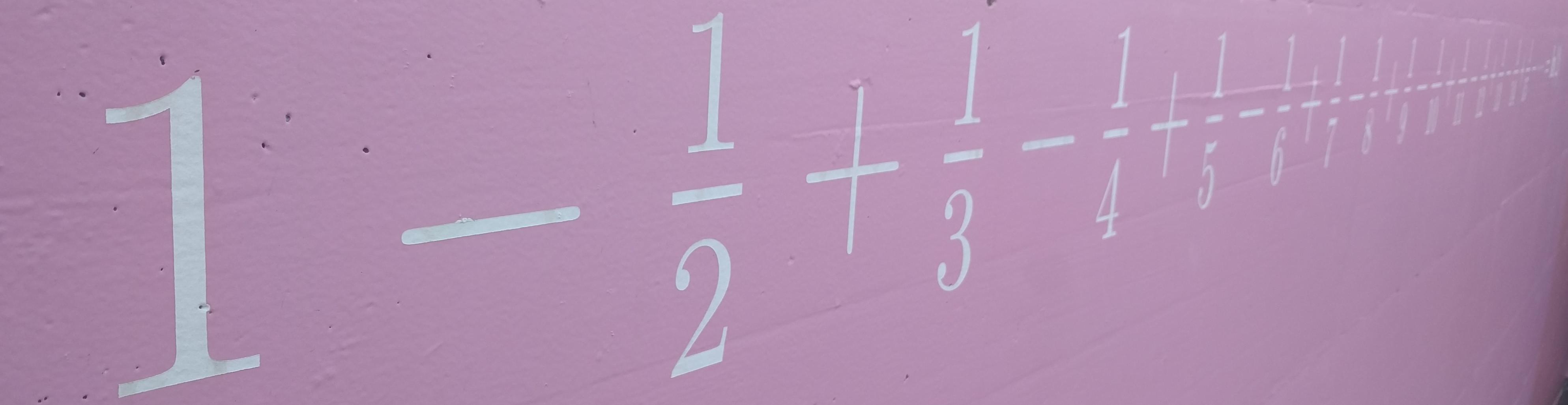Exemple: Étudions le développement de MacLaurin de \(f(x)=e^x\).

Puisque \(f^{(k)}(x)=e^x\) pour tout \(k\), \(f\in C^\infty(I)\), avec \(I=\mathbb{R}\). Pour tout \(n\) fixé, son \(DL(n)\) autour de \(0\) est donné par \[ e^{x}=1+x+\frac{x^2}{2!}+\frac{x^3}{3!}+\cdots+\frac{x^n}{n!} +R_n(x)\,, \] où \(R_n(x)=x^n\varepsilon_n(x)\), avec \[ \varepsilon_n(x)=x\frac{e^u}{(n+1)!}\,, \] où \(u\) est un nombre entre \(0\) et \(x\). Voyons si on peut prendre la limite \(n\to\infty\), en vérifiant les deux étapes décrites plus haut.

1. D'abord, la série de MacLaurin associée est \[ \sum_{k\geqslant 0}\frac{1}{k!}x^k\,. \] On a vu que cette série a un rayon de convergence infini, elle converge donc pour tout \(x\): \(I_s=\mathbb{R}\).
2. Ensuite, pour calculer la limite du reste, on commence par l'estimer comme suit: \(\forall x\in \mathbb{R}\), \[\begin{aligned} |R_n(x)|=|x^n\varepsilon_n(x)|&=\Bigl|x^{n+1}\frac{e^u}{(n+1)!} \Bigr|\\ &\leqslant |x|^{n+1}\frac{e^{|u|}}{(n+1)!}\\ &\leqslant e^{|x|}\frac{|x|^{n+1}}{(n+1)!} \end{aligned}\] Dans cette dernière inégalité, on a utilisé le fait que \(u\) est entre \(0\) et \(x\), et donc \(|u|\leqslant |x|\). Maintenant, puisque \(x\) est fixé, le critère de d'Alembert (pour les suites) implique que \[\lim_{n\to\infty}\frac{|x|^{n+1}}{(n+1)!}=0\,,\] on a donc bien que le reste tend vers zéro: \(\lim_{n\to \infty}R_n(x)=0\), pour tout \(x\in I_r=\mathbb{R}\).

Exemple: Considérons le sinus hyperbolique, \[ \sinh(x):= \frac{e^x-e^{-x}}{2}\,. \] Puisqu'on a déjà la série de Taylor de \(e^{x}\), et que celle-ci converge pour tout \(x\in \mathbb{R}\), il suffit d'écrire \[\begin{aligned} \sinh(x) &=\frac{1}{2}(e^x-e^{-x})\\ &=\frac{1}{2} \Bigl( \sum_{k\geqslant 0}\frac{x^k}{k!} - \sum_{k\geqslant 0}\frac{(-x)^k}{k!} \Bigr)\\ &= \sum_{k\geqslant 0}\frac{1}{k!}\frac{(1-(-1)^k)}{2}x^k\,. \end{aligned}\] Mais puisque \[\frac{1-(-1)^k}{2}= \begin{cases} 0&k \text{ pair,}\\ 1&k \text{ impair,}\\ \end{cases} \] seuls les termes d'indices impairs demeurent. On a donc \[ \boxed{\sinh(x) =x+\frac{x^3}{3!}+\frac{x^5}{5!}+\cdots =\sum_{k\geqslant 0}\frac{x^{2k+1}}{(2k+1)!}\,,\qquad \forall x\in \mathbb{R} } \] De même pour le cosinus hyperbolique, \[\cosh(x):=\frac{e^x+e^{-x}}{2}\,,\] \[ \boxed{\cosh(x) =1+\frac{x^2}{2!}+\frac{x^4}{4!}+\cdots =\sum_{k\geqslant 0}\frac{x^{2k}}{(2k)!}\,,\qquad \forall x\in \mathbb{R} } \]

Exemple: Considérons le développement de MacLaurin de \(f(x)=\sin(x)\in C^\infty(\mathbb{R})\). On peut écrire ses dérivées de façon compacte, \[ f^{(n)}(x)=\sin(x+n\tfrac{\pi}{2})\,, \] ce qui donne \(f^{(n)}(0)=\sin(n\frac{\pi}{2})\). On a donc que toutes les dérivées d'ordre pair sont nulles, \(f^{(2k)}(0)=0\), alors que \(f^{(2k+1)}(0)=(-1)^k\), ce qui donne une série de Taylor \[ \sum_{k\geqslant 0} \frac{(-1)^k}{(2k+1)!}x^{2k+1}\,. \] On vérifie facilement que cette série converge pour tout \(x\in I_s:= \mathbb{R}\). Le reste étant \(R_n(x)=x^{n+1}\frac{f^{(n+1)}(u)}{(n+1)!}\), et puisque \(|f^{(n+1)}(u)|\leqslant 1\), on a aussi que \(R_n(x)\to 0\) pour tout \(x\in I_r:= \mathbb{R}\). Ceci montre que la série de Taylor décrit \(f\) sur toute la droite: \[ \boxed{ \sin(x)=x-\frac{x^3}{3!}+\frac{x^5}{5!}-\cdots=\sum_{n\geqslant 0}\frac{(-1)^n}{(2n+1)!}x^{2n+1}\,,\qquad \forall x\in \mathbb{R} } \] On peut procéder de même pour montrer que \[ \boxed{ \cos(x)=1-\frac{x^2}{2!}+\frac{x^4}{4!}-\cdots=\sum_{n\geqslant 0}\frac{(-1)^n}{(2n)!}x^{2n}\,,\qquad \forall x\in \mathbb{R} } \]

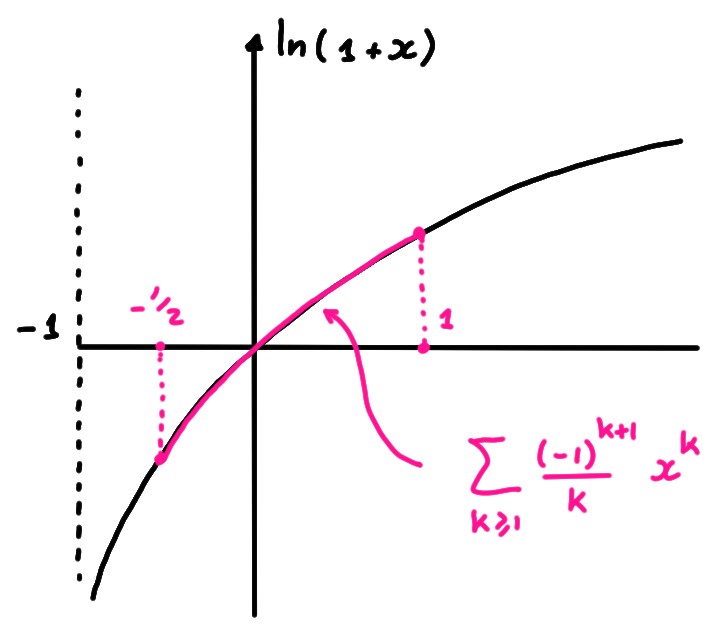
Exemple: Considérons \(f(x)=\log(1+x)\), définie sur \(I=]-1,+\infty[\). Sur \(I\), \(f\) est infiniment dérivable, et ses dérivées sont données par \[ f^{(k)}(x)=(-1)^{k+1}(k-1)!(1+x)^{-k}\,. \] Ainsi, sa série de MacLaurin est \[ \sum_{k\geqslant 1}\frac{(-1)^{k+1}}{k}x^k\,, \] et on a vu que l'intervalle de convergence de cette série entière est \(I_s:= ]-1,1]\),

L'étude du reste est plus délicate. Si \(x\in I_s\), \[\begin{aligned} |R_n(x)|&=|x^n\varepsilon_n(x)|\\ &=\Bigl| x^{n+1} \frac{f^{(n+1)}(u)}{(n+1)!} \Bigr|\\ &=\frac{1}{n+1} \Bigl|\frac{x}{1+u}\Bigr|^{n+1} \end{aligned}\] On voit que pour tendre vers zéro, il faut s'assurer que \(|\frac{x}{1+u}|\leqslant 1\). Distinguons les cas. D'une part, si \(x\geqslant 0\), alors \(u\geqslant 0\), et donc \[\left|\frac{x}{1+u}\right|=\frac{x}{1+u}\leqslant x\leqslant 1\,, \] ce qui permet d'écrire \[ |R_n(x)|\leqslant \frac{1}{n+1}\to 0\quad \text{ lorsque }n\to\infty\,. \] D'autre part, si \(-1\lt x\leqslant 0\) alors \(1+u\geqslant 1+x \gt 0\) et donc \[ \left|\frac{x}{1+u}\right|=\frac{-x}{1+u}\leqslant\frac{-x}{1+x}\,. \] Donc pour garantir \(|\frac{x}{1+u}|\leqslant 1\), on peut imposer \(\frac{-x}{1+x}\leqslant 1\), qui est équivalent à \(x\geqslant -\frac12\). Donc \(R_n(x)\to 0\) dès que \(x\in I_r:= [-\frac12,1]\). Ainsi, on a montré que \[ \boxed{\log(1+x)= \sum_{k\geqslant 1}\frac{(-1)^{k+1}}{k}x^k\,,\quad \forall x\in [-\tfrac12,1]} \]

Exemple: On peut montrer que pour tout \(x\in \mathbb{R}\), \[ \boxed{ \arctan(x)=x-\frac{x^3}{3}+\frac{x^5}{5}-\frac{x^7}{7}+\cdots= \sum_{k\geqslant 0}(-1)^{k}\frac{x^{2k+1}}{2k+1}\,. } \]

Exemple: Considérons \[ f(x)= \begin{cases} e^{-\frac1{x^2}}&\text{ si }x\neq 0\\ 0&\text{ si }x=0\,. \end{cases} \] Clairement, \(f\) est infiniment dérivable partout en dehors de \(x=0\). En travaillant un peu plus (laissé en exercice), on peut montrer que \(f\) est également infiniment dérivable en \(x=0\), et que ses dérivées en ce point sont toutes nulles: \[ f^{(k)}(0)=0\qquad \forall k\geqslant 1\,. \] On en déduit que le \(DL(n)\) en \(x_0=0\) existe, et est donnée par \[ f(x)=\underbrace{0+0\cdot x+0\cdot x^2+\cdots +0\cdot x^n}_{=0} +\underbrace{R_n(x)}_{=f(x)} \] On en déduit que sa série de MacLaurin est la série entière dont tous les termes sont nuls; elle converge donc en tout \(x\in \mathbb{R}\), mais ne représente évidemment pas la fonction...