Analyse 1 | S. Friedli (EPFL)

11.3 Séries entières et représentation de fonctions

Revenons à notre problème initial, qui était de prendre la limite \(n\to \infty\) pour une fonction qui possède, pour tout \(n\), un \(DL(n)\).

Soit \(I\) un intervalle ouvert, \(f\) une fonction définie sur \(I\), et \(x_0\in I\) un point fixé.

On sait, depuis la formule de Taylor, que si \(f\) est de classe \(C^{n}\) sur \(I\), alors elle possède un \(DL(n)\) en \(x_0\). Donc si on veut que \(f\) possède des développements limités de tous les ordres, on peut imposer qu'elle soit infiniment dérivable sur \(I\).

L'ensemble des fonctions infiniment dérivables sur \(I\) est défini par \[ C^\infty(I):=\bigl\{f:I\to \mathbb{R}\,\big|\,f\in C^k(I)\,\,\forall k\geqslant 1 \bigr\} \]

Exemple: Les fonctions fondamentales, telles que polynômes, fonctions trigonométriques, exponentielles et logarithmes, sont toutes infiniment dérivables sur leur domaine de définition.

Donc si \(f\in C^\infty(I)\), elle possède un développement limité à tous les ordres en \(x_0\), dont les coefficients sont donnés par \(a_k=\frac{f^{(k)}(x_0)}{k!}\): \[\begin{aligned} f(x)&= f(x_0)+ f'(x_0)(x-x_0)+R_1(x)\\ f(x)&= f(x_0)+ f'(x_0)(x-x_0)+ \tfrac{f^{(2)}(x_0)}{2!}(x-x_0)^2+R_2(x)\,.\\ f(x)&= f(x_0)+ f'(x_0)(x-x_0)+ \tfrac{f^{(2)}(x_0)}{2!}(x-x_0)^2 +\tfrac{f^{(3)}(x_0)}{3!} (x-x_0)^3 +R_3(x)\,.\\ \vdots & \\ f(x)&= f(x_0)+ f'(x_0)(x-x_0)+ \tfrac{f^{(2)}(x_0)}{2!}(x-x_0)^2 +\tfrac{f^{(3)}(x_0)}{3!} (x-x_0)^3 \cdots +\tfrac{f^{(n)}(x_0)}{n!}(x-x_0)^n +R_n(x)\,.\\ \vdots & \end{aligned}\] Nous allons maintenant décrire les contraintes à imposer pour garantir que dans la limite \(n\to\infty\), les parties principales permettent de reconstruire entièrement \(f(x)\).

On l'a déjà dit, dans la limite, les parties principales donnent naissance à une série entière: \[ \lim_{n\to\infty} \sum_{k=0}^n\frac{f^{(k)}(x_0)}{k!}(x-x_0)^k = \sum_{k= 0}^\infty\frac{f^{(k)}(x_0)}{k!}(x-x_0)^k\,,\] Il sera donc essentiel de s'assurer que le \(x\) qu'on considère appartient à l'intervalle de convergence de cette série.

Mais ça n'est pas encore suffisant: on voudra aussi que la limite des restes soit nulle, pour le \(x\) qu'on considère: \[ \lim_{n\to\infty}R_n(x)=0 \]

Le procédé peut donc être résumé de la façon suivante:

On calculera le rayon de convergence \(R\) et l'intervalle de convergence de la série entière \[\sum_{k= 0}^\infty\frac{f^{(k)}(x_0)}{k!}(x-x_0)^k\,,\] noté \(I_s\).
On déterminera tous les \(x\in I\) pour lesquels \(\lim_{n\to\infty}R_n(x)=0\); on notera \(I_r\) l'ensemble de ces \(x\).

Rappelons qu'à \(n\) fixé, \(R_n(x)\) étant le reste du \(DL(n)\) de \(f\) autour de \(x_0\), \[\lim_{x\to x_0}R_n(x)=0\,.\] Mais ici, ce que l'on fait est différent: on fixe un \(x\) proche de \(x_0\), et on demande que \[\lim_{n\to \infty}R_n(x)=0\,.\]

Si ces deux étapes peuvent être vérifiées rigoureusement, on aura montré que sur l'ensemble \[I':= I\cap I_s\cap I_r\,.\] \(f\) peut être représentée à l'aide de la série \[ f(x)= \sum_{k= 0}^\infty\frac{f^{(k)}(x_0)}{k!}(x-x_0)^k\,\qquad \forall x\in I'\,, \] appelée série de Taylor (ou développement de Taylor). Lorsque \(x_0=0\), on l'appelle série de MacLaurin (ou développement de MacLaurin).

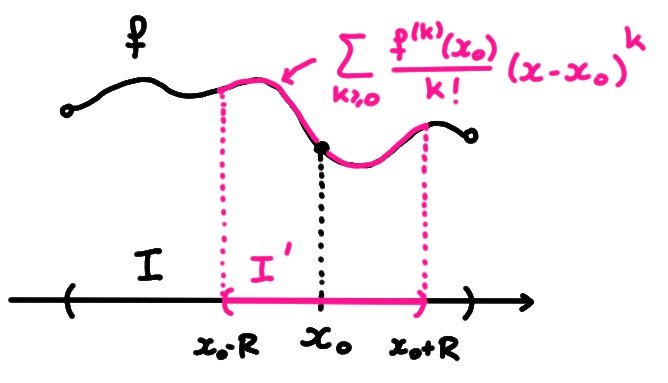
Une fonction infiniment dérivable \(f\), définie au voisinage du point \(x_0\), possède un développement de Taylor (DT) en \(x_0\) si elle peut être représentée par sa série de Taylor dans ce voisinage: \[ f(x)= \sum_{k= 0}^\infty\frac{f^{(k)}(x_0)}{k!}(x-x_0)^k\,. \]

Si la fonction peut effectivement être représentée par sa série de Taylor, cela signifie qu'elle peut être entièrement reconstruite, dans un voisinage de \(x_0\), à l'aide de la connaissance de toutes ses dérivées en \(x_0\).