On se représente souvent l'ensemble des nombres réels, noté \(\mathbb{R}\), comme tous les points d'une droite:

On se représente souvent l'ensemble des nombres réels, noté \(\mathbb{R}\), comme tous les points d'une droite:

Même si cette image est
utile pour l'intuition (en particulier pour se représenter des distances
ou comparer des grandeurs),
elle ne constitue évidemment pas une définition rigoureuse.
En particulier, elle n'exprime pas le fait que
les réels se prêtent bien au calcul, à savoir à la
manipulation abstraite de quantités, qu'elles
soient positives ou négatives, (très) petites ou (très) grandes.
De plus, les concepts fondamentaux de l'analyse (limite,
continuité, dérivabilité, intégrabilité)
se définissent précisément à l'aide de quelques notions simples
qui utilisent toute la structure des réels.
Donc avant de commencer à présenter l'analyse à proprement parler,
on se doit de définir quelles sont exactement les propriétés qui caractérisent
\(\mathbb{R}\).
On listera en particulier les règles de calcul qui donneront aux réels la
structure de ce qu'on appelle un corps.
La construction des nombres commence, en général, avec l'introduction des nombres naturels/entiers, avec lesquels on peut déjà compter (''un mouton, deux moutons, trois moutons, ...''): \[ \mathbb{N}:=\{0,1,2,3,4,\dots\}\,. \]
Puis viennent s'ajouter les entiers relatifs, obtenus à partir de \(\mathbb{N}\) en rajoutant toutes les quantités entières négatives (''il fait froid: \(-15\) degrés!'', ou ''\(3-7=-4\)''): \[ \mathbb{Z}:=\{\dots,-4,-3,-2,-1,0,1,2,3,4,\dots\}\,. \]
L'étape suivante est de considérer en plus toutes les proportions possibles entre deux grandeurs entières (''un demi litre de lait'', ''une heure et quart'', ''deux tiers des étudiants'',...), pour obtenir les nombres rationnels: \[ \mathbb{Q}=\bigl\{\tfrac{p}{q}\,\big|\,p,q\in \mathbb{Z}\,,q\neq 0\bigr\}\,. \] Les rationnels contiennent \(\mathbb{Z}\) (prendre \(q=1\)), donc ils contiennent des nombres arbitrairement grands, et peuvent être utilisés pour décrire des grandeurs astronomiques. Mais ils contiennent aussi des quotients aussi petits que l'on veut (\(\frac1{10}=0.1\), \(\frac1{100}=0.01\), etc.), et peuvent donc être utilisés pour décrire des grandeurs atomiques ou subatomiques.
Pourquoi, alors, ne pas se contenter de garder \(\mathbb{Q}\) pour faire de l'analyse?
Même s'il permet a priori de mesurer des grandeurs à
toutes les échelles possibles nécessaires de l'univers,
\(\mathbb{Q}\) souffre d'un défaut
majeur: il ne permet pas de tout mesurer!
En effet,
beaucoup de grandeurs physiques sont des quantités irrationnelles.
Voyons deux exemples.
Le nombre \(\pi\) est défini comme la longueur de la circonférence d'un disque dont le diamètre est égal à \(1\):
Il est surprenant d'apprendre que le développement décimal de ce nombre ne présente pas de régularité apparente: \[ \pi=3.1415926535897932384626433\dots \] On peut facilement trouver des rationnels qui approximent \(\pi\) à un niveau essentiellement arbitraire de précision (les décimales en rouge indiquent à partir d'où le rationnel cesse de donner une bonne approximation): \[\begin{aligned} \frac{22}{7}&=3.14{\color{red}285714286...}\\ \frac{333}{106}&=3.1415{\color{red}0943396...}\\ \frac{103993}{33102}&=3.141592653{\color{red}01...} & \text{etc.} \end{aligned}\] Pourtant, Johann Heinrich Lambert a montré en 1761 que \(\pi\) est irrationnel: il n'existe aucune paire \(p,q\in \mathbb{N}^*\) telle que \[\pi=\frac{p}{q}\,.\] Pour une preuve relativement courte, mais qui requiert beaucoup des notions d'analyse présentées dans ce cours, voir cette vidéo, ou encore celle-ci (les deux présentent la même preuve de l'irrationnalité de \(\pi\), due à Niven).
Bien avant la preuve de Lambert,
un problème géométrique encore plus simple montrait de manière embarrassante
l'importance des irrationnels:
L'école Pythagoricienne (env. 500BC) avait observé le fait suivant.
Considérons un triangle rectangle dont les deux cathètes ont longueur \(1\):
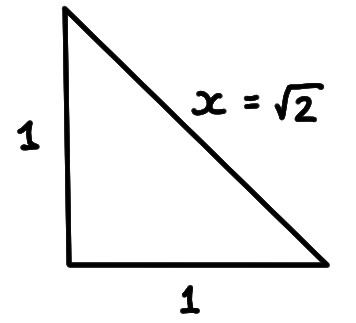
La longueur de l'hypothénuse est donnée par la solution \(x>0\) de l'équation \[x^2=1^2+1^2=2\,.\]
Lemme: Le nombre \(x\), solution de l'équation \(x^2=2\), est irrationnel.
On démontre l'affirmation par l'absurde.
Supposons que \(x\in\mathbb{Q}\), à savoir
qu'il existe des entiers \(p\) et \(q\) tels
\(x\) peut s'écrire \(x=\frac{p}{q}\).
On peut en fait supposer que \(p\) et \(q\) sont premiers
entre eux, c'est-à-dire qu'ils
n'ont aucun diviseur commun (s'ils ont un diviseur commun, on peut toujours
simplifier la fraction).
Mais si \(x=\frac{p}{q}\), alors
\(x^2=\bigl(\frac{p}{q}\bigr)^2=2\), c'est-à-dire \(p^2=2q^2\), ce qui
implique que \(p^2\) est pair (un multiple de \(2\)), et
donc que \(p\) est pair aussi (exercice!).
On peut alors écrire \(p\) sous la forme \(p=2e\), où \(e\)
est un entier. Ceci implique également que
\(q^2=\frac{p^2}{2}=2e^2\), et donc \(q\), par le même argument qu'avant, est
aussi
pair. Ceci implique que \(p\) et \(q\) sont tous deux divisibles par \(2\), ce
qui représente une
contradiction, puisqu'on a supposé que \(p\) et \(q\) n'avaient aucun diviseur
commun.
Étant irrationnel, l'expansion décimale \(\sqrt{2}\)
n'a pas de ''fin'', et
ne présente aucun motif particulier (pas de périodicité, etc.):
\[
\sqrt{2}=1.414213562373095048801688724209\dots
\]
De nos jours, on connaît plus de
dix mille milliards de décimales
de cette expansion.
Sans surprise, la circonférence du disque et l'hypothénuse du triangle
sont loin d'être les seuls irrationnels, donc
cette discussion montre que même si \(\mathbb{Q}\) constitue un ensemble de nombres
allant des échelles subatomiques à superastronomiques, il ne contient pas tous
les nombres nécessaires pour faire de la géométrie élémentaire.
'' On sait que les nombres de ce genre (en parlant de \(\sqrt{2}\)) ont tourmenté Pythagore et son école presque jusqu'à puisement. Étant accoutumés à des nombres si étranges depuis notre première enfance, nous devons prendre garde à ne pas sous-estimer l'intuition mathématique de ces anciens sages. Leur tourment était hautement honorable. Ils se rendaient compte qu'on ne peut trouver aucune fraction dont le carré soit exactement égal à \(2\). On peut en donner des approximations très approchées, comme par exemple \(\frac{17}{12}\), dont le carré, \(\frac{289}{144}\), est très proche de \(\frac{288}{144}\), c'est à dire de \(2\). On peut s'approcher encore plus près de \(2\) en considérant des fractions constituées au moyen de nombres plus grands que \(17\) et \(12\), mais on n'atteindra jamais exactement \(2\). ''E. Schrödinger, Physique quantique et représentation du monde
Et en fait, dans un sens que nous ne détaillerons pas ici, il y a beaucoup plus d'irrationnels qu'il n'y a de rationnels...
Il y a donc, dans la construction d'un bon ensemble de nombres, une
étape finale, qui consiste à compléter
\(\mathbb{Q}\) en lui ajoutant tous
les irrationnels pour obtenir \(\mathbb{R}\). Cette construction est délicate, et
nous ne la décrirons pas en détails car elle sortirait du cadre de ce cours.
Mais ce que nous ferons, dans les sections suivantes, sera de définir \(\mathbb{R}\)
en listant ses propriétés.
Nous dirons d'abord que c'est,
comme \(\mathbb{Q}\), un ensemble
dans lequel on peut faire de l'arithmétique, c'est à dire des calculs à l'aide
d'opérations telles que addition et multiplication.
Puis nous exigerons de \(\mathbb{R}\) une propriété additionnelle,
naturelle mais délicate à formuler (voir
supremum et infimum plus loin),
qui le distinguera radicalement de \(\mathbb{Q}\), et qui nous permettra de
commencer à construire l'analyse.
(En passant, nous montrerons que dans \(\mathbb{R}\), l'existence de
\(\sqrt{2}\) est bien garantie.)
Remarque: Ce que nous ne ferons pas, c'est de montrer qu'on peut effectivement construire un ensemble \(\mathbb{R}\) jouissant de toutes ces propriétés. Pour plus de détails sur la construction des réels, je renvoie le lecteur aux livres d'analyse plus avancés.
Deux références pour le lecteur intéressé: