12.1 Introduction
Le problème original du calcul intégral était de calculer des aires, des
longueurs et des volumes, pour des objets géométriques du plan ou de l'espace,
plus compliqués que les formes simples de la géométrie, tels que triangles,
rectangles, cercles, parallélépipèdes, sphères, ...
Plus tard, surtout après les travaux de Newton et Leibniz à la fin du XIIXème
siècle, le calcul intégral permettait d'aller bien plus loin que le
calcul des aires et de volumes, trouvant des applications à la mécanique,
thermodynamique, etc., plus tard à la théorie des probabilités, puis à tous les
domaines des sciences.
Aires de régions simples
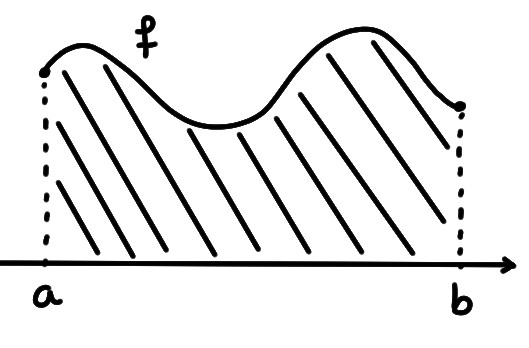
Nous nous concentrerons, dans cette introduction,
sur des régions particulières du plan, limitées par le
graphe d'une fonction et un axe.
Donc dans
cette section nous traiterons uniquement des fonctions dont les valeurs
sont positives; dans les sections suivantes on passera au cas plus général.
On va donc considérer une fonction sur un intervalle fermé et borné,
\(f:[a,b]\to \mathbb{R}\), telle que
\[ f(x)\geqslant 0 \qquad \forall x\in [a,b]
\]
On considérera la région délimitée par le graphe de \(f\), par l'axe \(Ox\), et
par les deux droites verticales \(x=a\) et \(x=b\):
Commençons par un cas très simple mais très important:
Exemple:
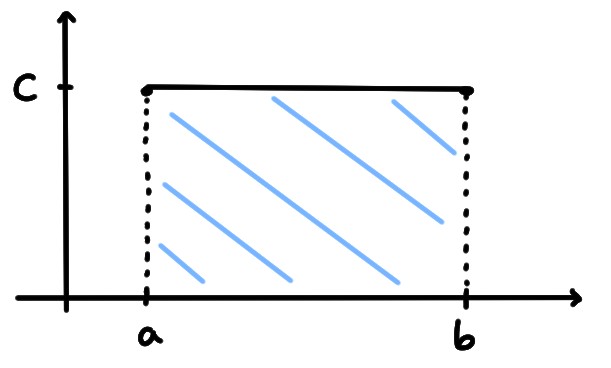
Considérons une droite horizontale, c'est-à-dire une
fonction constante, \(f(x)=C\) \(\forall x\in [a,b]\), où \(C\)
est constante strictement positive.
Dans ce cas, la région en question est un rectangle, et l'aire se calcule par
\[ \text{aire}=\text{base}\times\text{hauteur}=(b-a)\times C=C(b-a)\,.\]
Exemple:
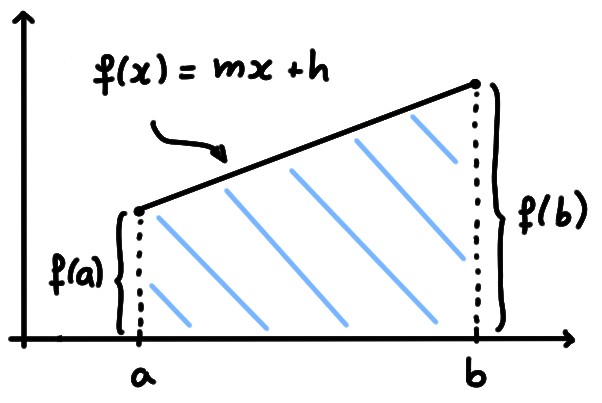
Si on considère maintenant la région délimitée par une droite de pente
non-nulle, d'équation
\[y=f(x)=mx+h\,\qquad \forall x\in [a,b]\,,\]
positive en tout point de \([a,b]\),
alors la région considérée est un trapèze (si d'aventure \(f(a)=0\) ou
\(f(b)=0\), c'est un triangle),
dont on calcule l'aire en faisant
\[\begin{aligned}
\text{aire}&=\text{moyenne des bases}\times\text{hauteur}\\
&=\frac{f(a)+f(b)}{2}\times (b-a)\\
&=\frac{(ma+h)+(mb+h)}{2}\times (b-a)\\
&=\frac{1}{2}m(b^2-a^2)+h(b-a)\,.
\end{aligned}\]
Exemple:
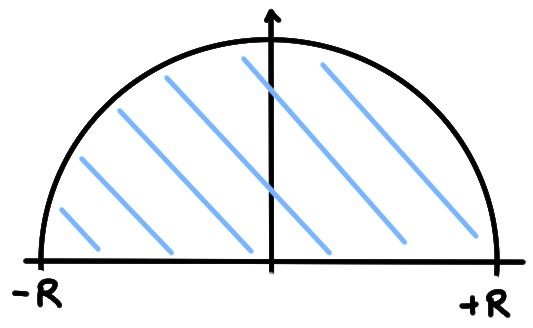
Finalement, si on considère
\[
f(x):= \sqrt{R^2-x^2}\qquad \forall x\in [-R,R]\,,
\]
alors la région considérée est un demi-disque de rayon \(R\),
et donc son aire est
\[ \text{aire}=\frac12 \pi R^2\,.
\]
Les exemples ci-dessus font partie des quelques cas de figures
géométriques du plan dont on peut calculer l'aire sans avoir recours au calcul
intégral.