Analyse 1 | S. Friedli (EPFL)

13.2 Type I

En guise d'introduction, considérons le problème suivant: comment intégrer une fonction continue, mais définie sur un intervalle qui n'est pas fermé, par exemple de la forme \(\left]a,b\right]\)?

Supposons donc que \(f:\left]a,b\right]\to\mathbb{R}\) est continue en tout point \(x_0\in \left]a,b\right[\), et que \(f\) est continue à gauche en \(b\). Lorsque \(f\) possède une limite à droite en \(a\), on peut la prolonger par continuité, et ensuite définir son intégrale au sens classique d'une fonction continue sur \([a,b]\).

Exemple: Considérons \(f(x)=x\log(x)\) sur \(\left]0,1\right]\), qui est bien continue. Puisque \[ \lim_{x\to 0^+}f(x)=0\,, \] On peut définir \[ \widetilde{f}(x):= \begin{cases} x\log(x)&\text{ si }0\lt x\leqslant 1\,,\\ 0&\text{ si } x=0\,,\\ \end{cases} \] et définir l'intégrale de \(f\) sur \(\left]0,1\right]\) comme l'intégrale de \(\widetilde{f}\) sur \([0,1]\). Puisque \(\widetilde{f}\) est continue, cette intégrale est bien définie. Puisque \[ \int x\log(x)\,dx = \frac{x^2}{2}\log(x)-\frac{x^2}{4}+C \] on peut considérer \[ \widetilde{F}(x)= \begin{cases} \frac{x^2}{2}\log(x)-\frac{x^2}{4}&\text{ si }0\lt x\leqslant 1\,,\\ 0&\text{ si }x=0\,, \end{cases} \] qui est une primitive de \(\widetilde{f}\) continue sur \([0,1]\). Ainsi, par le Théorème Fondamental, \[\begin{aligned} \int_0^1\widetilde{f}(x)\,dx =\widetilde{F}(1)-\widetilde{F}(0)=-\frac{1}{4}\,. \end{aligned}\]

Lorsque \(f\) n'a pas de limite lorsque \(x\to a^+\), \(f\) ne peut pas être prolongée par continuité.

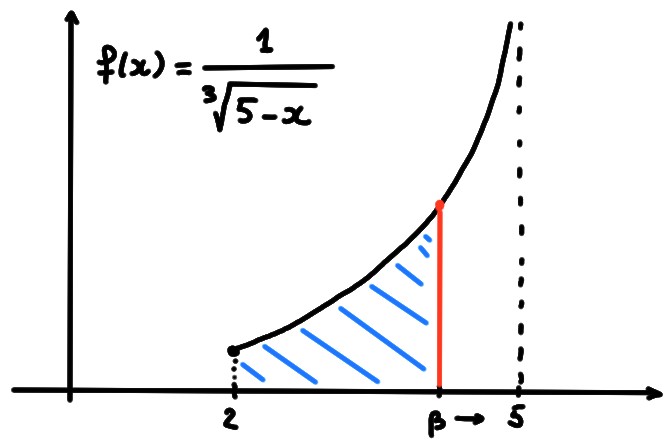
Exemple: Considérons \(f:]0,1]\to \mathbb{R}\), définie par \[ f(x)=\frac{1}{\sqrt{x}}\,,\] et essayons de calculer l'aire sous son graphe:

Le problème avec cette fonction est qu'elle n'est pas bornée, puisque \[ \lim_{x\to 0^+}f(x)=+\infty\,. \] Par conséquent, il n'est même pas clair que l'aire sous son graphe soit bien définie. On ne peut pas mettre en place la méthode classique d'intégration au sens de Riemann/Darboux: la somme de Darboux supérieure a son premier rectangle qui est toujours de hauteur infinie! Donc cette fonction ne peut pas s'intégrer de manière naïve, en sommant simplement des aires de rectangles, et on ne peut pas donner le sens classique au symbole ''\(\int_0^1\frac{1}{\sqrt{x}}\,dx\)''.

L'idée, pour intégrer cette fonction, va être de traiter le problème en \(x=0\) en utilisant un processus de limite.

En effet, si on fixe un nombre quelconque \(0\lt \varepsilon\lt 1\), petit, on peut restreindre \(f\) à l'intervalle \([\varepsilon,1]\). Comme \(f:[ \varepsilon,1]\to\mathbb{R}\) est continue (et par conséquent bornée), on peut l'intégrer de façon standard, et même utiliser le théorème fondamental: \[ \int_\varepsilon^1f(x)\,dx= \int_\varepsilon^1\frac{1}{\sqrt{x}}\,dx =2\sqrt{x}\,\Bigr|^1_\varepsilon=2(1-\sqrt{\varepsilon})\,. \] Cette intégrale dépend de \(\varepsilon\), mais elle se comporte bien lorsque \(\varepsilon\) s'approche de zéro (par la droite).

On peut en fait prendre la limite \(\varepsilon\to 0^+\), pour donner un sens à l'intégrale de \(f\) sur \(]0,1]\), au sens d'une limite: \[ \lim_{\varepsilon\to 0^+} \int_\varepsilon^1\frac{1}{\sqrt{x}}\,dx =2\,. \]

Ça peut paraître contre-intuitif: la région délimitée par le graphe de la fonction de ce dernier exemple n'est pas ''limitée'': elle s'étend infiniment loin le long de l'axe des \(y\gt 0\). Pourtant, son aire est finie: on pourrait la recouvrir entièrement à l'aide d'une quantité finie de peinture! Ceci est dû au fait que lorsque \(x\to 0^+\), \(f(x)\) tend vers l'infini mais ''pas trop vite''.

Ce phénomène est semblable à celui rencontré dans l'étude des séries convergentes, où il est possible de sommer une infinité de nombres strictement positifs, et obtenir une somme totale finie.

L'idée utilisée dans ce dernier exemple peut se généraliser:

Soit \(f\colon\left]a,b\right]\to \mathbb{R}\) telle que pour tout \(a\lt \alpha\lt b\), \(f\) soit continue sur \([\alpha,b]\). Si la limite \[ \int_{a^+}^bf(x)\,dx:= \lim_{\alpha\to a^+}\int_{\alpha}^bf(x)\,dx= \lim_{\varepsilon\to 0^+}\int_{a+\varepsilon}^bf(x)\,dx \] existe et est finie, on l'appelle l'intégrale généralisée de type I, et on dit qu'elle converge. Si la limite est \(\pm\infty\), ou si elle n'existe pas, on dit que l'intégrale généralisée diverge.
Soit \(f\colon\left[a,b\right[\to \mathbb{R}\) telle que pour tout \(a\lt \beta\lt b\), \(f\) soit continue sur \([a,\beta]\). Si la limite \[ \int_{a}^{b^-}f(x)\,dx := \lim_{\beta\to b^-}\int_{a}^\beta f(x)\,dx= \lim_{\varepsilon\to 0^+}\int_{a}^{b-\varepsilon}f(x)\,dx \] existe et est finie, on l'appelle l'intégrale généralisée de type I, et on dit qu'elle converge. Si la limite est \(\pm\infty\), ou si elle n'existe pas, on dit que l'intégrale généralisée diverge.

Exemple: Considérons l'intégrale généralisée de \(f(x)=\frac1x\) sur l'intervalle \(]0,1]\): \[\begin{aligned} \int_{0^+}^1\frac1x\,dx&= \lim_{\varepsilon \to 0^+}\int_{\varepsilon}^1\frac1x\,dx\\ &= \lim_{\varepsilon \to 0^+}\log (x)\Bigr|^1_\varepsilon\\ &= \lim_{\varepsilon \to 0^+}(-\log (\varepsilon))\\ &=+\infty\,, \end{aligned}\] donc l'intégrale diverge.

Dans ce dernier exemple, \(f(x)=\frac1x\) tend vers \(+\infty\) lorsque \(x\to 0^+\), ''trop vite'' pour que son intégrale généralisée soit finie.

Exemple: L'intégrale généralisée de \(f(x)=\frac{1}{\sqrt[3]{5-x}}\) sur \([2,5[\) converge, car \[\begin{aligned} \int_2^{5^-}\frac{1}{\sqrt[3]{5-x}} &= \lim_{\beta\to 5^-} \int_2^\beta\frac{1}{\sqrt[3]{5-x}}\\ &= \lim_{\beta\to 5^-} -\frac32(5-x)^{2/3}\Big|_2^{\beta}\\ &= \lim_{\beta\to 5^-} \frac32\Bigl\{3^{2/3}-(5-\beta)^{2/3}\Bigr\}\\ &= \frac{3^{5/3}}{2}\,. \end{aligned}\]

Remarquons que \(\lim_{x\to 5^{-}}f(x)=+\infty\).

Un critère de comparaison

Dans beaucoup de situations pratiques, on doit déterminer si une intégrale généralisée de type I converge ou diverge, sans se préoccuper de connaître sa valeur (au cas où elle converge). Pour ça, on aimerait éviter de passer par la connaissance de la primitive de \(f\), en utilisant une comparaison. On peut le faire si la fonction est de signe constant:

Soient \(f,g\colon\left]a,b\right]\to \mathbb{R}\) continues sur tout intervalle \([\alpha,b]\), \(a\lt \alpha \lt b\), et telles que \[ 0\leqslant f(x)\leqslant g(x)\qquad \forall x\in \left]a,b\right]\,. \] Alors:

Si \(\displaystyle \int_{a^+}^bg(x)\,dx\) converge, alors \(\displaystyle\int_{a^+}^bf(x)\,dx\) converge aussi.
Si \(\displaystyle\int_{a^+}^bf(x)\,dx=+\infty\) (diverge), alors \(\displaystyle\int_{a^+}^bg(x)\,dx=+\infty\) (diverge aussi).

Preuve:

Si on fixe \(a\lt \alpha\lt b\), alors par la propriété de l'intégrale classique, \[\int_\alpha^b f(x)\,dx\leqslant \int_\alpha^b g(x)\,dx\,.\] Remarquons que les deux côtés de cette inégalité sont des fonctions positives, monotones décroissantes en \(\alpha\). Puisque \(\int_\alpha^bg(x)\,dx\) est majorée par sa limite lorsque \(\alpha\to a^+\), qui est finie et vaut \(\int_{a^+}^bg(x)\,dx\), ceci implique aussi que \[\int_\alpha^b f(x)\,dx\leqslant \int_{a^+}^b g(x)\,dx\,.\] On obtient la première affirmation en prenant la limite \(\alpha\to a^+\) dans cette inégalité.

La deuxième se démontre de la même façon, en prenant d'abord la limite \(\alpha\to a^+\) dans \(\int_\alpha^bf(x)\,dx\).

Remarque: Remarquons que ce résultat est l'analogue continu direct du critère de comparaison pour les séries.

Exemple: Étudions la convergence de l'intégrale généralisée \[ \int_{1^+}^2\frac{1}{\sqrt{x^3-1}}\,dx\,. \] Le calcul de la primitive de \(\frac{1}{\sqrt{x^3-1}}\) étant hardu, on cherche plutôt à faire une comparaison avec l'intégrale d'une autre fonction, plus simple.

En effet, pour tout \(x\in ]1,2]\), on peut factoriser \(x^3-1\), \[ 0\leqslant f(x)=\frac{1}{\sqrt{x^3-1}} =\frac{1}{\sqrt{(x-1)(\underbrace{x^2+x}_{\geqslant 0}+1)}}\leqslant \frac{1}{\sqrt{x-1}}=g(x)\,. \] Mais maintenant, \[ \int_{1^+}^2g(x)\,dx= \lim_{\alpha\to 1^+}\int_{\alpha}^2g(x)\,dx= \lim_{\alpha\to 1^+}2\sqrt{x-1}\Bigr|^2_\alpha=2\quad(\text{converge})\,. \] Donc l'intégrale de \(f\) converge aussi.

On a donc montré que \(\int_{1^+}^2\frac{1}{\sqrt{x^3-1}}\,dx\) converge, sans avoir eu besoin de calculer une primitive de \(\frac{1}{\sqrt{x^3-1}}\).

Intégrales du type \(\displaystyle \int_{0^+}^b\frac{dx}{x^q}\)

On a vu dans les exemples que si \[ \lim_{x\to 0^+}f(x)=+\infty\,, \] alors la convergence/divergence de intégrale généralisée \(\int_{0^+}^bf(x)\,dx\) va dépendre de la ''vitesse'' à laquelle \(f(x)\) tend vers l'infini à l'approche de \(0^+\). Dans le cas des fonctions du type \(f(x)=\frac{1}{x^q}\), on peut distinguer exactement les cas en fonction de la valeur de l'exposant \(q\):

Théorème: Pour tout \(b\gt 0\), \[ \int_{0^+}^b\frac{dx}{x^q}= \begin{cases} \frac{b^{1-q}}{1-q}\text{ (converge)}& \text{ si }q\lt 1\,,\\ +\infty\text{ (diverge)}& \text{ si }q\geqslant 1\,. \end{cases} \]

Preuve:

On a déjà vu le cas \(q=1\) dans un exemple, donc on considère \(q\neq 1\). Fixons \(0\lt \alpha \lt b\). Par un calcul explicite de la primitive, \[ \int_{\alpha}^b\frac{dx}{x^q} = \frac{1}{1-q}\Bigl\{ \frac{1}{b^{q-1}}- \frac{1}{\alpha^{q-1}} \Bigr\} \] Puis il suffit de remarquer que

si \(q\gt 1\), alors \(\lim_{\alpha\to 0^+}\frac{1}{\alpha^{q-1}}= +\infty\), et
si \(q\lt 1\), alors \(1-q\gt 0\), et donc \( \lim_{\alpha\to 0^+}\frac{1}{\alpha^{q-1}} =\lim_{\alpha\to 0^+}\alpha^{1-q}=0\),

ce qui conclut la preuve.

Exemple: Considérons \[ \int_{0^+}^{\frac{\pi}{4}}\frac{1}{x^2\cos(x)}\,dx\,, \] qui est généralisée puisque \(\lim_{x\to 0^+}\frac{1}{x^2\cos(x)}=+\infty\). Comme \(0\lt \cos(x)\leqslant 1\) pour tout \(x\in ]0,\frac{\pi}{4}]\), on peut utiliser la comparaison \[ \int_{0^+}^{\frac{\pi}{4}}\frac{1}{x^2\cos(x)}\,dx\geqslant \int_{0^+}^{\frac{\pi}{4}}\frac{1}{x^2}\,dx=+\infty\,, \] puisque dans cette dernière, \(q=2\gt 1\).

Un critère via une limite de quotient

Une conséquence de la proposition énoncée plus haut:

Soient \(f,g:]a,b]\to \mathbb{R}_+\), continues, telles que \[ \lim_{x\to a^+}\frac{f(x)}{g(x)}=L\gt 0\,. \] Alors \(\displaystyle \int_{a^+}^bf(x)\,dx\) converge si et seulement si \(\displaystyle \int_{a^+}^bg(x)\,dx\) converge.

(Il existe bien sûr une affirmation analogue pour \(\displaystyle \int_{a}^{b^-}f(x)\,dx\).)

Preuve:

Par l'existence et positivité de la limite, il existe \(\delta\gt 0\) tel que \[ \frac{L}{2}\leqslant \frac{f(x)}{g(x)}\leqslant \frac{3L}{2}\,,\qquad \forall x\in ]a,a+\delta[\,. \] On a donc \[ 0\lt \frac{L}{2}g(x)\leqslant f(x) \leqslant \frac{3L}{2}g(x)\,,\qquad \forall x\in ]a,a+\delta[\,, \] d'où on peut obtenir les comparaisons voulues, à l'aide du critère de comparaison énoncé plus haut.

Exemple: Étudions la convergence de l'intégrale généralisée \[ \int_{-1^+}^1\frac{\sin(\tfrac{\pi}{2} x^2)}{\sqrt{x+1}}\,dx\,. \] Cette intégrale est bien généralisée puisque \(\lim_{x\to -1^+}f(x)=+\infty\). Pourtant, on remarque que ce qui fait tendre \(f\) vers l'infini, c'est la présence de \(\frac{1}{\sqrt{x+1}}\): le sinus ne pose pas de problème (à part pour le calcul de la primitive). Si on pose \[ g(x):= \frac{1}{\sqrt{x+1}}\,, \] alors \[\begin{aligned} \int_{-1^+}^1g(x) &=\lim_{\alpha\to -1^+} \int_{\alpha}^1\frac{1}{\sqrt{x+1}}\,dx\\ &=2\lim_{\alpha\to -1^+} \bigl(\sqrt{2}-\sqrt{\alpha+1}\bigr)\\ &=2\sqrt{2}\,. \end{aligned}\] Et comme \[ \lim_{x\to -1^+}\frac{f(x)}{g(x)}= \lim_{x\to -1^+}\sin(\tfrac{\pi}{2} x^2)=1\gt 0\,, \] l'intégrale généralisée de \(f\) converge aussi.

Exemple: L'exemple vu précédemment, \(\int_{1^+}^2\frac{1}{\sqrt{x^3-1}}\,dx\), peut aussi se traiter en utilisant la proposition. Posons \[ g(x)=\frac{1}{\sqrt{x-1}}\,, \] qui comme on sait a une intégrale généralisée sur \(]1,2]\) convergente (puisque \(q=\frac{1}{2}\lt 1\)). On remarque alors que \[ \lim_{x\to {1^+}}\frac{f(x)}{g(x)}= \lim_{x\to 1^+}\sqrt{\frac{x-1}{x^3-1}}= \lim_{x\to 1^+}\sqrt{\frac{1}{x^2+x+1}}=\frac{1}{\sqrt{3}}\gt 0\,, \] on en déduit, par la proposition, que \(\int_{1^+}^2\frac{1}{\sqrt{x^3-1}}\,dx\) converge.