Rappelons que l'intégrale
a été définie pour des fonctions bornées, définies
sur un intervalle \([a,b]\), fermé et borné. Dans ce cadre,
la continuité s'est avérée
une condition suffisante pour garantir l'intégrabilité.
Dans cette section, nous allons étendre l'intégration à des fonctions définies
sur des intervalles où elle n'est plus forcément bornée, par exemple sur un
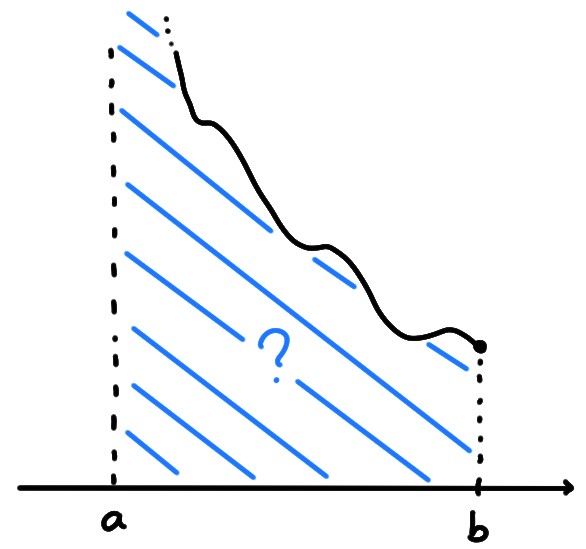
intervalle \(]a,b]\), possédant une asymptote verticale,
\[
\lim_{x\to a^+}f(x)=+\infty\,,
\]
ou alors sur des intervalles non-bornés, du type \([a,+\infty[\), tendant vers zéro, \[ \lim_{x\to\infty}f(x)=0\,. \]
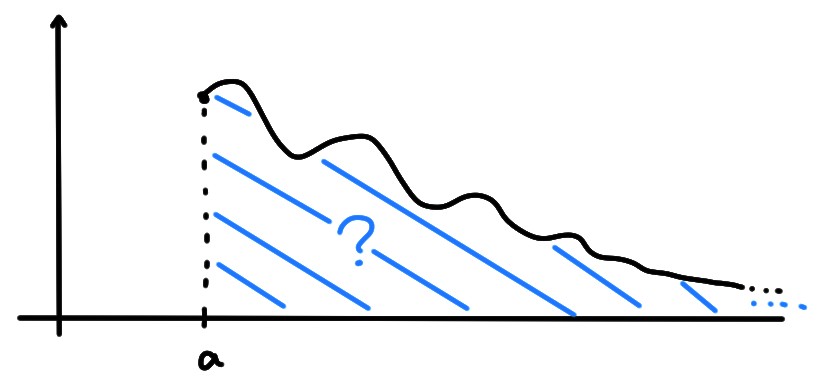
Des intégrales de ce type sont généralisées, puisqu'elles n'entrent pas dans le cadre de l'intégrale de Riemann/Darboux présentée jusqu'ici.
Dernière compilation: 2024-01-22 (20:49:38)
Sauf indication contraire, le contenu de ce document est soumis à une licence Creative Commons internationale, Attribution: Pas d'Utilisation Commerciale - Partage dans les Mêmes Conditions 4.0 (CC BY-NC-SA 4.0)
