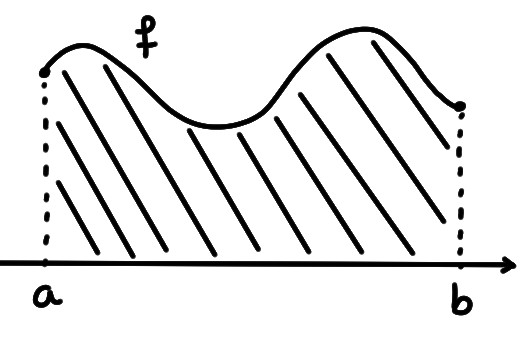
12.2 Définition de l'intégrale de Riemann-Darboux

Dans toute cette section, on fixera une fonction bornée \(f:[a,b]\to \mathbb{R}\).

Pour garder en tête l'interprétation en terme d'une ''aire sous la courbe'', les illustrations se feront la plupart du temps pour une fonction positive.

Pourtant, la construction de l'intégrale que l'on va donner ci-dessous est indépendante du signe de la fonction sur l'intervalle.

Subdivisions

L'idée générale de base de l'intégration est d'approximer un objet compliqué à l'aide d'une union d'objets simples. Dans l'intégrale d'une fonction, on approxime l'aire sous le graphe de \(f:[a,b]\to \mathbb{R}\) à l'aide de ''régions simples'' qui sont des rectangles.

La première étape est de diviser l'intervalle:

On appelle subdivision (aussi: partition) de l'intervalle \([a,b]\) toute collection ordonnée de nombres \[ a=x_0\lt x_1\lt x_2\lt \cdots \lt x_{n-1}\lt x_n=b\,. \] On notera en général une subddivision par la lettre \[\sigma=(x_0,x_1,x_2,\cdots,x_{n-1},x_n)\,.\]

Soit \(\sigma=(x_0,x_1,x_2,\cdots,x_{n-1},x_n)\) une subdivision de \([a,b]\). On définit, pour tout \(k\in \{1,\dots,n\}\), l'intervalle \[I_k:=[x_{k-1},x_k]\,.\]

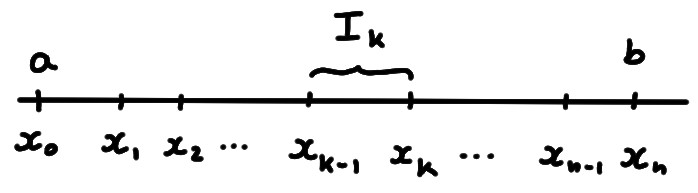
Notons qu'en général, les intervalles \(I_1,I_2,\dots,I_n\) ne sont pas forcément tous de même longueur.

On appelle subdivision régulière (à \(n\) éléments) de \([a,b]\) la subdivision dont les intervalles \(I_k\) ont tous taille \(\frac{b-a}{n}\), c'est-à-dire pour laquelle \(x_k=a+k\frac{b-a}{n}\): \[ \sigma=\bigl( a,a+\tfrac{b-a}{n}, a+2\tfrac{b-a}{n}, \dots, a+(n-1)\tfrac{b-a}{n}, b \bigr) \]

Une fois que l'on se donne une subdivision, on peut l'utiliser pour diviser la région sous le graphe de \(f\) en régions plus fines, qui commencent à ressembler à des rectangles:

Sommes de Darboux

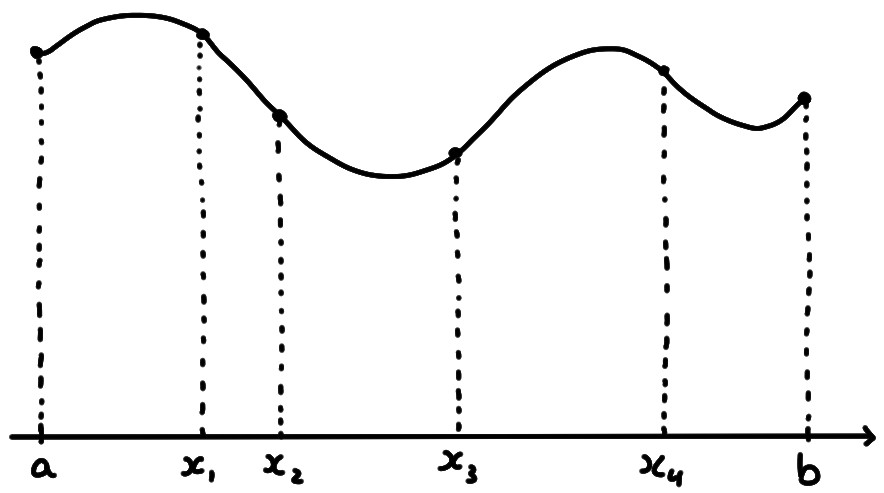
Pour une subdivision donnée \(\sigma=(x_0,x_1,x_2,\cdots,x_{n-1},x_n)\), introduisons pour tout \(k\in \{1,\dots,n\}\), les nombres \[ m_k:= \inf_{x\in I_k}f(x)\,,\qquad M_k:= \sup_{x\in I_k}f(x)\,, \] Puisqu'on suppose que \(f\) est bornée, ces nombres sont finis.

On peut alors définir deux sommes associées à la subdivision \(\sigma\):

Soit \(f:[a,b]\to \mathbb{R}\) une fonction bornée, et \(\sigma\) une subdivision de \([a,b]\). On définit:
  1. la somme de Darboux inférieure, \[ \underline{S}_\sigma(f):= \sum_{k=1}^nm_k(x_{k}-x_{k-1}) \,, \]
  2. la somme de Darboux supérieure \[ \overline{S}_\sigma(f):= \sum_{k=1}^nM_k(x_{k}-x_{k-1}) \,. \]

Par définition, \[ \underline{S}_\sigma(f)\leqslant \overline{S}_\sigma(f)\,. \] Considérons la fonction sur l'intervalle \(I_k=[x_{k-1},x_k]\). Dans le cas où \(f(x)\geqslant 0\), \(m_k(x_k-x_{k-1})\) (resp. \(M_k(x_k-x_{k-1})\)) représente l'aire d'un rectangle, dont le côté supérieur est situé en-dessous (resp. en-dessus) du graphe de \(f\).

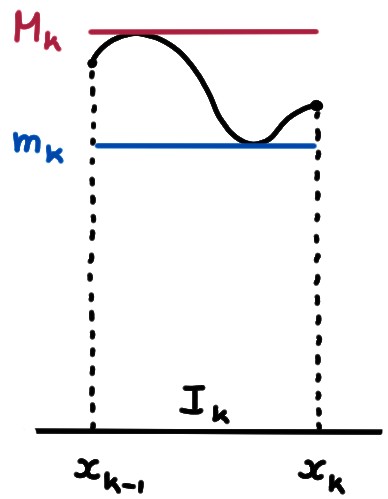
Donc sur \(I_k\), la vraie aire sous le graphe peut toujours être comparée aux aires de ces deux rectangles, ce qui a pour conséquence que globalement, l'aire sous la courbe peut être minorée et majorée par les sommes de Darboux: \[ \underline{S}_\sigma(f) \leqslant \text{aire} \leqslant \overline{S}_\sigma(f)\,. \]

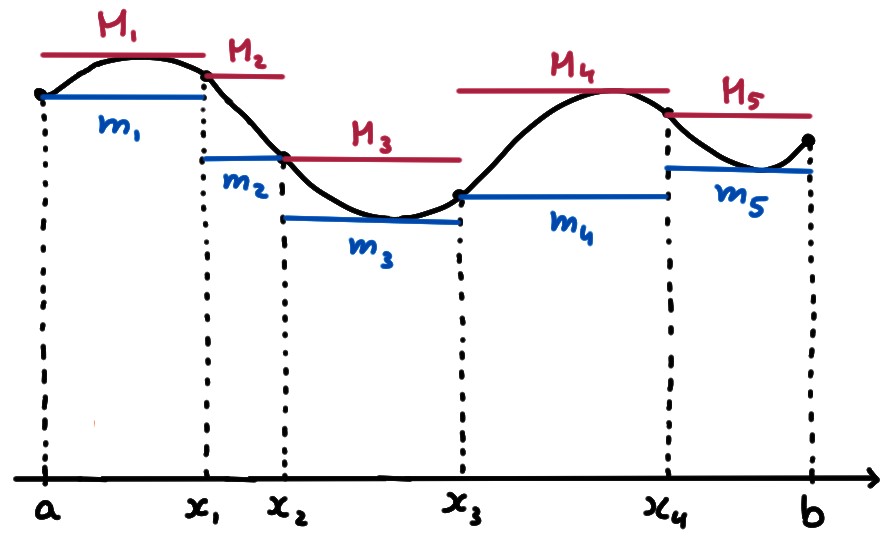
Voyons maintenant comment se comportent les sommes de Darboux lorsqu'on rajoute un point à la subdivision:

Lemme: Soit \(\sigma=(x_0,x_1,\dots,x_{k-1},x_k,\dots,x_n)\) une subdivision de \([a,b]\), et soit \(\sigma'=(x_0,x_1,\dots,x_{k-1},y,x_k,\dots,x_n)\) la subdivision obtenue en rajoutant un point \(y\) à \(\sigma\), entre \(x_{k-1}\) et \(x_k\). Alors \[ \underline{S}_{\sigma}(f) \leqslant \underline{S}_{\sigma'}(f) \leqslant \overline{S}_{\sigma'}(f) \leqslant \overline{S}_{\sigma}(f)\,. \]

A priori, \(\underline{S}_\sigma(f)\) et \(\overline{S}_\sigma(f)\) sont des nombres différents: \(\underline{S}_\sigma(f)\lt \overline{S}_\sigma(f)\). Mais le lemme ci-dessus nous dit qu'ils ne peuvent que se rapprocher lorsque l'on rajoute des points dans la subdivision. On s'attend donc à ce que pour des fonctions ''raisonnables'', il soit possible de rendre \(\underline{S}_\sigma(f)\) arbitrairement proche de \(\overline{S}_\sigma(f)\), en prenant une subdivision suffisamment fine:

Ceci motive la définition suivante:

Pour une fonction \(f:[a,b]\to \mathbb{R}\) bornée, on définit les nombres \[\begin{aligned} \underline{S}(f)&:= \sup_\sigma \underline{S}_\sigma(f)\,,\\ \overline{S}(f)&:= \inf_\sigma \overline{S}_\sigma(f)\,. \end{aligned}\] Si \(\underline{S}(f)=\overline{S}(f)\), on dit que \(f\) est intégrable au sens de Riemann/Darboux . On appelle le nombre \(S=\underline{S}(f)=\overline{S}(f)\equiv S\) l'intégrale de \(f\), et on le note \[S=\int_a^bf(x)\,dx\,.\] Par convention, on définit \[ \int_a^a f(x)\,dx:= 0\,. \]

Remarque: Le symbole \(\int_a^b f(x)\,dx\) représente un nombre, qui ne dépend pas du ''\(x\)'' qui apparaît deux fois. On appelle ce ''\(x\)'' une variable d'intégration. C'est une variable muette, dans le sens où elle est uniquement utilisée pour construire l'intégrale; l'intégrale n'en dépend pas explicitement. Donc on pourrait aussi écrire \[ I =\int_a^bf(z)\,dz =\int_a^bf(\alpha)\,d\alpha =\int_a^bf(m)\,dm=\cdots \] Les nombres \(a\) et \(b\) sont appelés bornes d'intégration.

À propos de la terminologie: Le symbole \(\int\), apparemment introduit par Newton, est une espèce de ''S'', qui peut rappeler l'origine de l'intégrale: ''somme''.

À strictement parler, l'intégrale au sens de Riemann passe par la définition des sommes de Riemann \[ S_\sigma^*(f)=\sum_{k=1}^nf(x_k^*)(x_k-x_{k-1})\,, \] où pour tout \(k=1,2,\dots,n\), \(x_k^*\) est un point quelconque choisi dans \(I_k=[x_{k-1},x_k]\). Ces sommes satisfont toujours \[\underline{S}_\sigma(f)\leqslant S_\sigma^*(f)\leqslant \overline{S}_\sigma(f)\,.\]

Quiz 12.2-1 : Soit \(f:[a,b]\to \mathbb{R}\) une fonction bornée, \(\sigma\) une subdivision de \([a,b]\), et \(\overline{S}_\sigma(f)\) et \(\underline{S}_\sigma(f)\) les sommes Darboux supérieures et inférieures. Vrai ou faux?
  1. \(\underline{S}_\sigma(f)\leqslant \overline{S}_\sigma(f)\).
  2. Si \(\underline{S}_\sigma(f)=\overline{S}_\sigma(f)\), alors \(f\) est intégrable.
  3. Si \(\underline{S}_\sigma(f)\lt \overline{S}_\sigma(f)\), alors \(f\) n'est pas intégrable.
  4. Si \(g:[a,b]\to \mathbb{R}\) est aussi bornée, telle que \(f(x)\leqslant g(x)\) pour tout \(x\in [a,b]\), alors \(\overline{S}_\sigma(f)\leqslant \overline{S}_\sigma(g)\).
  5. Si \(\sigma'\subset \sigma\), alors \(\overline{S}_{\sigma'}\geqslant \overline{S}_\sigma(f)\) et \(\underline{S}_{\sigma'}\leqslant \underline{S}_\sigma(f)\).
  6. Si \(\sup_\sigma \underline{S}_\sigma(f)=\inf_\sigma\overline{S}_\sigma(f)\), alors \(f\) est intégrable.

Dernière compilation: 2024-01-22 (20:49:38)

Sauf indication contraire, le contenu de ce document est soumis à une licence Creative Commons internationale, Attribution: Pas d'Utilisation Commerciale - Partage dans les Mêmes Conditions 4.0 (CC BY-NC-SA 4.0)