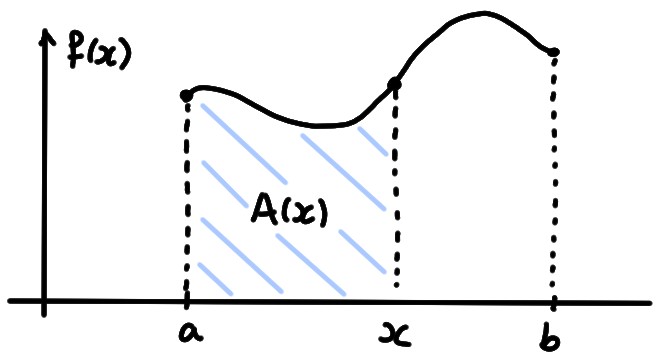
Comme son nom l'indique, \(A(x)\) peut être interprétée, lorsque \(f\) est positive, comme l'aire sous le graphe de \(f\), entre les droites verticales d'abscisses \(a\) et \(x\) respectivement. Cette aire dépend bien sûr du choix de \(x\):
Maintenant que l'on a défini l'intégrale et que l'on a étudié ses principales propriétés, revenons au problème plus appliqué, qui est celui de savoir comment calculer \(\int_a^bf(x)dx\).
Dans cette section, nous supposerons en général que \(f:[a,b]\to \mathbb{R}\) est continue.
Remarque: On a pris soin de nommer la variable d'intégration différemment (on a choisi ''\(t\)'', mais on aurait pu prendre n'importe quelle lettre différente de \(x\)), pour montrer que la dépendance de \(A(x)\) en \(x\) est dans la borne supérieure de l'intégrale.
Comme son nom l'indique, \(A(x)\) peut être interprétée, lorsque \(f\) est positive, comme l'aire sous le graphe de \(f\), entre les droites verticales d'abscisses \(a\) et \(x\) respectivement. Cette aire dépend bien sûr du choix de \(x\):
Par définition, on a \(A(a)=0\), et notre but est de calculer \(A(b)\).
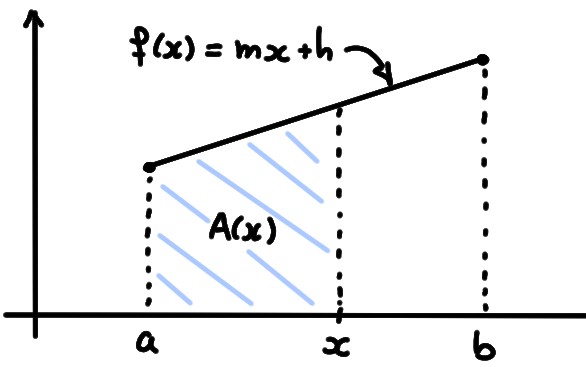
Exemple: Si \(f(x)=mx+h\), est positive sur \([a,b]\), alors \(A(x)\) est une aire de trapèze:
Cette propriété surprenante que l'on vient d'observer, à savoir que la dérivée de la fonction aire est égale à la fonction, est en fait toujours vraie...
Théorème: (Théorème Fondamental, première partie) Pour toute fonction \(f:[a,b]\to \mathbb{R}\) continue, \(x\mapsto A(x)\) est dérivable sur \(]a,b[\), et sa dérivée vaut \(f\): \[ A'(x)=f(x)\,\qquad \forall x\in ]a,b[\,. \]
Fixons \(x\in ]a,b[\), et montrons que \[\lim_{h\to 0^+} \frac{A(x+h)-A(x)}{h}=f(x)\,. \] D'abord, puisque \(a\lt x\lt x+h\), la relation de Chasles entraîne \[ A(x+h)=A(x)+\int_x^{x+h}f(t)\,dt\,, \] qui permet d'écrire \[ \frac{A(x+h)-A(x)}{h}= \frac1h \int_x^{x+h} f(t)dt\,. \] Maintenant, le Théorème de la Moyenne, appliqué à l'intégrale du membre de droite de cette dernière égalité, garantit l'existence d'un \(c_h\in ]x,x+h[\) tel que \[\frac1h \int_x^{x+h} f(t)dt=f(c_h)\,. \] Or lorsque \(h\to 0^+\), on a \(c_h\to x^+\), et comme \(f\) est continue en \(x\) cela donne \[ \lim_{h\to 0^+} \frac{A(x+h)-A(x)}{h}= \lim_{h\to 0^+} f(c_h)= \lim_{c\to x^+} f(c)=f(x)\,. \] On procède de même avec la limite \(h\to 0^-\), pour montrer que \[ \lim_{h\to 0^-} \frac{A(x+h)-A(x)}{h}= f(x)\,. \] Ceci montre donc que \(A'(x)\) existe et vaut \(f(x)\).
Les fonctions qui, comme \(A\), sont dérivables, et dont la dérivée vaut \(f\), portent un nom:
Exemple: Par exemple, \(F(x)=x-\frac{x^3}{3}\) est une primitive de \(f(x)=1-x^2\), puisque \[ F'(x)=\Bigl(x-\frac{x^3}{3}\Bigr)'=1-x^2=f(x)\qquad \forall x\,. \] Remarquons que \(G(x)=x-\frac{x^3}{3}+\frac{\pi^2}{6}\) est aussi une primitive de \(f(x)\), puisque la constante \(\frac{\pi^2}{6}\) a une dérivée nulle, et donc \(G'(x)=f(x)\).
On le voit dans ce dernier exemple: lorsqu'une fonction possède une primitive,
elle en possède une infinité, puisqu'on peut toujours ajouter une
constante arbitraire qui ne contribue pas à la dérivée.
Le lemme suivant a déjà été démontré précédemment (conséquence
du Théorème des accroissements finis,
ici).
Lemme: Soit \(I\) un intervalle ouvert, et soient \(F,G:I\to \mathbb{R}\) deux primitives de \(f\), alors il existe une constante \(C\) telle que \[ F(x)=G(x)+C \quad \forall x\in I\,. \]
Avant de poursuivre, une conséquence de ce qui précède:
Lemme: Si \(f:[a,b]\to\mathbb{R}\) est continue, alors \(A:[a,b]\to \mathbb{R}\) est continue.
La continuité en les points \(x_0\in ]a,b[\) suit de la dérivabilité démontrée plus haut. Il reste donc à vérifier la continuité sur le bord. Pour démontrer la continuité à droite en \(a\), on peut profiter du fait que \(f\) est bornée (puisqu'elle est continue): il existe une constante \(C\) telle que\(|f(t)|\leqslant C\) pour tout \(t\in [a,b]\). Par conséquent, \[|A(x)|= \Bigl|\int_a^xf(t)\,dt\Bigr|\leqslant \int_a^x|f(t)|\,dt\leqslant C\int_a^x\,dt=C|x-a|\,, \] qui implique \[ \lim_{x\to a^+}A(x)=0=A(a)\,. \] On montre de même que \(\lim_{x\to b^-}A(x)=A(b)\).
Théorème: (Théorème Fondamental, deuxième partie) Soit \(f:[a,b]\to \mathbb{R}\) continue, et soit \(F:[a,b]\to \mathbb{R}\) une primitive de \(f\) sur \(]a,b[\), continue sur \([a,b]\). Alors \[ \int_a^bf(x)\,dx=F(b)-F(a)\,. \]
Parfois, on utilisera aussi la notation \[ F(x)\Big|^b_a:= F(b)-F(a)\,. \]
On sait que la fonction aire \(A(x)=\int_a^xf(t)\,dt\) est une primitive de \(f\). Donc, par le lemme précédent, il existe une constante \(C\) telle que \(A(x)=F(x)+C\) pour tout \(x\in ]a,b[\). Par continuité, ceci implique aussi que \(A(a)=F(a)+C\) et \(A(b)=F(b)+C\). On trouve la valeur de \(C\) en remarquant que \(A(a)=0\), ce qui implique \(C=-F(a)\). On a donc \[ \int_a^bf(x)\,dx=A(b)=F(b)-F(a)\,.\]
Exemple: On a déjà vu une primitive de \(f(x)=1-x^2\): \(F(x)=x-\frac{x^3}{3}\). On peut donc recalculer l'aire sous la parabole d'Archimède: \[\begin{aligned} \int_{-1}^1(1-x^2)\,dx&=F(1)-F(-1)\\ &= \Bigl( 1-\frac{1^3}{3} \Bigr) - \Bigl( (-1)-\frac{(-1)^3}{3} \Bigr)\\ &=\frac43\,. \end{aligned}\]
Le Théorème Fondamental a montré que le calcul d'une intégrale peut, en
principe, se réduire à un calcul de primitive. Or la recherche d'une primitive
peut souvent représenter un
travail considérable, même pour des fonctions simples.
Nous allons donc, après avoir dit quelques généralités,
passer un certain temps à décrire quelques-unes de
méthodes classiques de calcul de primitives, appelées aussi
méthodes d'intégration.
Dernière compilation: 2024-10-05 (22:34:29)
Sauf indication contraire, le contenu de ce document est soumis à une licence Creative Commons internationale, Attribution: Pas d'Utilisation Commerciale - Partage dans les Mêmes Conditions 4.0 (CC BY-NC-SA 4.0)
