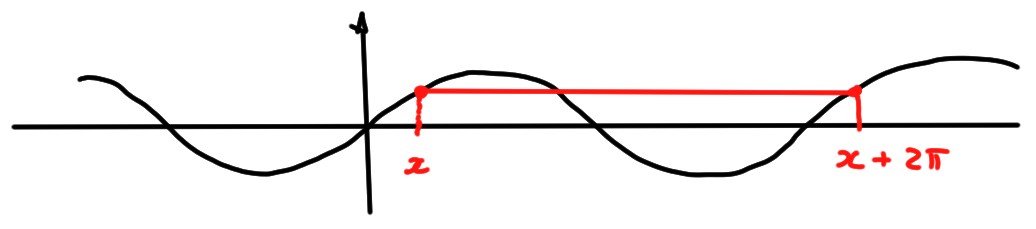
Exemple: \(f(x)=\sin (x)\) est périodique, de période \(T=2\pi\):
Remarque: Si \(f\) est \(t\)-périodique, elle est aussi \(\pm 2t\)-périodique, \(\pm 3t\)-périodique, etc.
Exemple: \(f(x)=\sin (x)\) est périodique, de période \(T=2\pi\):

Exemple: \(f(x)=\tan (x)\) (sur son domaine) est \(\pi\)-périodique car \[ \tan(x+\pi) =\frac{\sin(x+\pi)}{\cos(x+\pi)}=\frac{-\sin(x)}{-\cos(x)}=\tan(x)\,. \]
Exemple: Considérons une fonction constante: \(f(x)=C\). On a bien \(f(x+t)=f(x)\) pour tout \(x\) et tout \(t\gt 0\), donc \(f\) est \(t\)-périodique pour tout \(t>0\). Mais comme il n'existe pas de plus petit \(t\) strictement positif avec cette propriété, la fonction n'a pas de ''période'' à proprement parler.
Exemple:
Considérons la fonction
\[
f(x)=
\begin{cases}
1&\text{ si }x\in \mathbb{Q}\,,\\
0&\text{ si }x\in \mathbb{R}\setminus\mathbb{Q}\,.
\end{cases}
\]
Montrons que si \(t\in \mathbb{Q}\) est
un rationnel quelconque, alors \(f\) est \(t\)-périodique.
En effet, prenons un \(x\in \mathbb{R}\) quelconque. Si \(x\in \mathbb{Q}\), alors \(f(x)=1\),
et comme \(x+t\in \mathbb{Q}\), on a aussi \(f(x+t)=1\).
Si \(x\in \mathbb{R}\setminus\mathbb{Q}\), alors \(f(x)=0\),
et comme \(x+t\in\mathbb{R}\setminus \mathbb{Q}\), on a aussi \(f(x+t)=0\).
Dans tous les cas, \(f(x+t)=f(x)\).
Ici aussi, comme il n'existe pas de ''plus petit rationnel \(t\gt 0\)'', \(f\)
n'a pas de période.
Remarquons qu'en général, la somme de deux fonctions périodiques n'est pas forcément périodique!
Exemple: \(f(x)=\sin(2\pi x)\) est périodique, de période \(T_f=1\), et \(g(x)=\sin(\sqrt{2}\pi x)\) est périodique, de période \(T_g=\sqrt{2}\). Par contre, \(f+g\) n'est pas périodique, puisque \(\sqrt{2}\) étant irrationnel, aucun multiple de \(T_g\) ne coïncidera avec un multiple de \(T_f\).
On peut garantir que \(f+g\) est aussi périodique, mais en imposant une condition particulière sur \(T_f\) et \(T_g\):
Lemme: Soit \(f:\mathbb{R}\to\mathbb{R}\) périodique, de période \(T_f\), et \(g:\mathbb{R}\to\mathbb{R}\) périodique, de période \(T_g\). Alors \(f+g\) et \(f-g\) sont périodiques si \(\frac{T_f}{T_g}\in \mathbb{Q}\).
Si \(\frac{T_f}{T_g}\in \mathbb{Q}\), il existe deux entiers \(p,q\) tels que \(\frac{T_f}{T_g}=\frac{p}{q}\). Ceci signifie que \(qT_f=pT_g\). Ceci implique que si on définit \(\tilde{t}=q T_f\), alors pour tout \(x\), \[\begin{aligned} (f\pm g)(x+\tilde{t})=f(x+\tilde{t})\pm g(x+\tilde{t})&= f(x+q T_f)\pm g(x+q T_f)\\ &=\underbrace{f(x+q T_f)}_{=f(x)}\pm \underbrace{g(x+p T_g)}_{=g(x)}\\ &=(f\pm g)(x)\,, \end{aligned}\] ce qui implique que \(f\pm g\) est périodique.
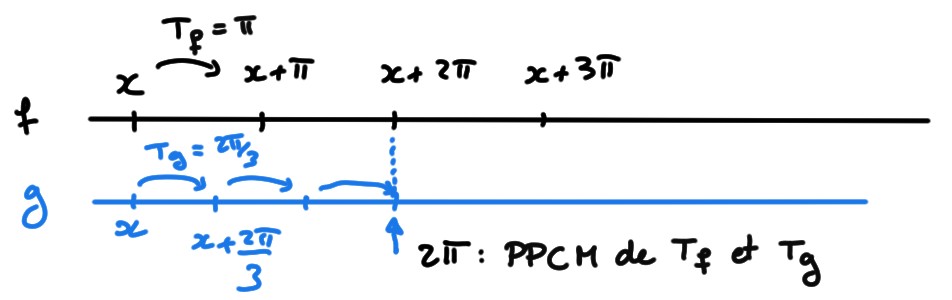
Exemple: La fonction \(f(x)=\sin^2(x)\) a pour période \(T_f=\pi\), et \(g(x)=\cos(3x)\) a pour période \(T_g=\frac{2\pi}{3}\). Comme \[ \frac{T_f}{T_g}=\frac{3}{2}\in \mathbb{Q}\,, \] on conclut par le lemme que \(f+ g\) et \(f-g\) sont périodiques. Mais comment calculer les périodes de ces fonctions?