Analyse 1 | S. Friedli (EPFL)

7.4 Limites latérales \(x\to x_0^\pm\)

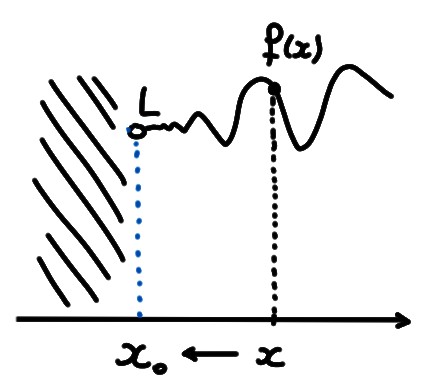
On parle alors de limite latérale si les valeurs d'une fonction tendent vers une valeur lorsqu'on s'approche d'un point \(x_0\) en maintenant le signe de \(x-x_0\) constant:

Soit \(x_0\in \mathbb{R}\).

Soit \(f\) une fonction définie sur un intervalle de la forme \(]x_0,x_0+\alpha[\) (\(\alpha\gt 0\)). On dit que \(f\) tend vers \(L\in \mathbb{R}\) lorsque \(x\) tend vers \(x_0\) par la droite si pour tout \(\varepsilon\gt 0\) il existe \(\delta\gt 0\) tel que \(|f(x)-L|\leqslant \varepsilon\) dès que \(0\lt x-x_0\leqslant \delta\), c'est-à-dire \(x_0\lt x\leqslant x_0+\delta\). On notera: \[\boxed{ \lim_{x\to x_0^+}f(x)=L\,.} \]
Soit \(f\) une fonction définie sur un intervalle de la forme \(]x_0-\alpha,x_0[\) (\(\alpha\gt 0\)). On dit que \(f\) tend vers \(L\in \mathbb{R}\) lorsque \(x\) tend vers \(x_0\) par la gauche si pour tout \(\varepsilon\gt 0\) il existe \(\delta\gt 0\) tel que \(|f(x)-L|\leqslant \varepsilon\) dès que \(-\delta\leqslant x-x_0\lt 0\), c'est-à-dire \(x_0-\delta\leqslant x\lt x_0\). On notera: \[\boxed{\lim_{x\to x_0^-}f(x)=L\,.} \]

Donc une fonction peut par exemple posséder une limite latérale à droite en \(x_0\), sans être du tout définie à gauche de \(x_0\):

Exemple: Par exemple, \(f(x)=\sqrt{x}\) est définie seulement sur \(\mathbb{R}_+=[0,+\infty[\), et \[ \lim_{x\to 0^+}f(x)=0\,. \]

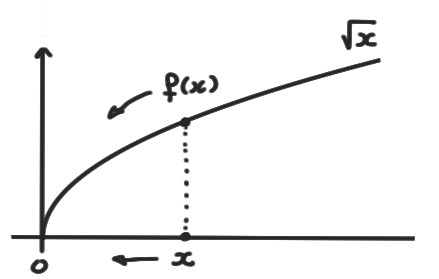
En effet, pour tout \(\varepsilon\gt 0\), on a \(|f(x)|=\sqrt{x}\leqslant \varepsilon\) si et seulement si \(x\leqslant \varepsilon^2\), et donc on peut prendre \(\delta:= \varepsilon^2\).

Mais une fonction peut être définie de part et d'autre de \(x_0\), et n'avoir qu'une seule limite latérale:

Exemple: Considérons, sur \(\mathbb{R}^*\), la fonction \[ f(x):= \begin{cases} 1-x^2&\text{ si }x\lt 0\,,\\ \pi&\text{ si }x=0\,,\\ \sin(1/x)&\text{ si }x\gt 0\,. \end{cases} \] Alors \(f\) n'a pas de limite à droite en \(x_0=0\), comme on sait, mais \[\lim_{x\to 0^-}f(x)=1\,.\]

Intuitivement, si les limites latérales en un point existent et sont égales, alors la vraie limite en ce point existe et prend la même valeur:

Théorème: Soit \(f\) définie dans un voisinage épointé de \(x_0\). Les deux affirmations ci-dessous sont équivalentes:

\(\displaystyle\lim_{x\to x_0}f(x)=L\)
\(\displaystyle\lim_{x\to x_0^+}f(x)=\lim_{x\to x_0^-}f(x)=L\)

Preuve:

Supposons que \(\lim_{x\to x_0}f(x)=L\), c'est-à-dire que pour tout \(\varepsilon\gt 0\) il existe un \(\delta\gt 0\) tel que \(|f(x)-L|\leqslant \varepsilon\) dès que \(0\lt |x-x_0|\leqslant \delta\). Or \(0\lt x-x_0\leqslant \delta\) et \(-\delta\leqslant x-x_0\lt 0\) impliquent évidemment \(0\lt |x-x_0|\leqslant \delta\). Et donc \(\lim_{x\to x_0^+}f(x)=\lim_{x\to x_0^-}f(x)=L\)
Maintenant, supposons que \(\lim_{x\to x_0^+}f(x)=\lim_{x\to x_0^-}f(x)=L\), et fixons \(\varepsilon\gt 0\). On a d'une part l'existence d'un \(\delta_->0\) tel que \(|f(x)-L|\leqslant \varepsilon\) dès que \(-\delta_-\leqslant x-x_0\lt 0\), et d'autre part l'existence d'un \(\delta_+>0\) tel que \(|f(x)-L|\leqslant \varepsilon\) dès que \(0\lt x-x_0\leqslant \delta_+\). En prenant \(\delta:= \min\{\delta_-,\delta_+\}\), on garantit que si \(0\lt |x-x_0|\leqslant \delta\), alors \(-\delta_-\leqslant x-x_0\lt 0\) et \(0\lt x-x_0\leqslant \delta_+\), et donc dans tous les cas, \(|f(x)-L|\leqslant \varepsilon\).

Il existe naturellement une version latérale du Théorème des deux gendarmes, ou du théorème sur l'équivalence avec les limites par des sous-suites, dans le cas des limites latérales.

Exemple: Considérons \[ f(x)=x\left\lfloor\frac1x \right\rfloor\,, \] qui est bien définie en tout \(x\neq 0\). Pour calculer sa limite lorsque \(x\to 0\), commençons par rappeler que par la définition de valeur entière, \[ \frac1x -1\lt \left\lfloor\frac1x \right\rfloor \leqslant \frac1x\,,\qquad \forall x\neq 0\,. \] On utilise cette double inégalité pour étudier les limites latérales en zéro:

Si on la multiplie des deux côtés par \(x\gt 0\), \[ \underbrace{x\left(\frac1x -1\right)}_{=1-x}\lt f(x) \leqslant \underbrace{x\cdot\frac1x}_{=1}\,,\qquad \forall x\gt 0\,. \] Puisque \(\lim_{x\to 0^+}(1-x)=1\), le Théorème des deux gendarmes (en version ''latérale'') implique que \[ \lim_{x\to 0^+}f(x)=1\,. \]
Si on la multiplie des deux côtés par \(x\lt 0\), \[ \underbrace{x\left(\frac1x -1\right)}_{=1-x} \gt f(x) \geqslant \underbrace{x\cdot\frac1x}_{=1}\,,\qquad \forall x\lt 0\,. \] Puisque \(\lim_{x\to 0^-}(1-x)=1\), le Théorème des deux gendarmes (en version ''latérale'') implique que \[ \lim_{x\to 0^-}f(x)=1\,. \]

Puisque les limites larérales existent et sont égales, \[ \lim_{x\to 0}f(x)=1\,. \]

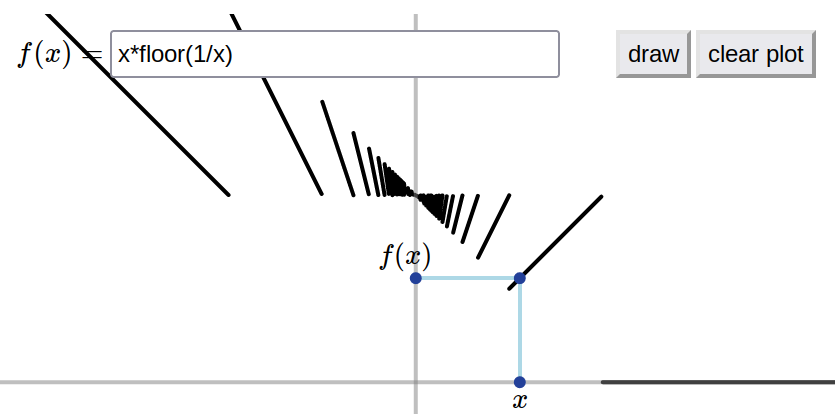
Le théorème précédent est aussi utile pour montrer qu'une limite \(x\to x_0\) n'existe pas. Pour ce faire, on pourra

montrer qu'une des limites latérales, \(x\to x_0^+\) ou \(x\to x_0^-\), n'existe pas, ou
montrer que les limites latérales \(x\to x_0^+\) et \(x\to x_0^-\), existent mais ont des valeurs différentes.

Exemple: Considérons \[ f(x)=\frac{|x^2-1|}{x-1}\,, \] et montrons que la limite \(\displaystyle\lim_{x\to 1}f(x)\) n'existe pas.

D'abord, remarquons que \(|x^2-1|=|x-1|\cdot|x+1|\). Ensuite, si \(x\) est proche de \(1\), alors \(|x+1|=x+1\), mais \[ |x-1|= \begin{cases} +(x-1)&\text{ si }x>1\,,\\ -(x-1)&\text{ si }x<1\,. \end{cases} \] On peut donc facilement calculer les limites latérales: \[ \lim_{x\to 1^-}f(x)= \lim_{x\to 1^-}\frac{-(x-1)(x+1)}{x-1}= \lim_{x\to 1^-}-(x+1)=-2\,, \] \[ \lim_{x\to 1^+}f(x)= \lim_{x\to 1^+}\frac{(x-1)(x+1)}{x-1}= \lim_{x\to 1^+}(x+1)=2\,, \] Comme les limites latérales existent mais sont inégales, on conclut que \(f(x)\) n'a pas de limite lorsque \(x\to 1\).

Quiz 7.4-1 : Vrai ou faux?

Si \(\lim_{x\to x_0^+}f(x)\) et \(\lim_{x\to x_0^-}f(x)\) existent, alors \(\lim_{x\to x_0}f(x)\) existe.
Si \(f\) est impaire et si \(\lim_{x\to 0^+}f(x)=L\), alors \(\lim_{x\to 0^-}f(x)=-L\).
Si \(f\) est paire, alors \(\lim_{x\to 0^+}f(x)\) existe et est égale à \(\lim_{x\to 0^-}f(x)\).
Si \(\lim_{x\to 0^+}f(x)=L\) et \(\lim_{x\to 0^-}f(x)=-L\), alors \(f\) est impaire.