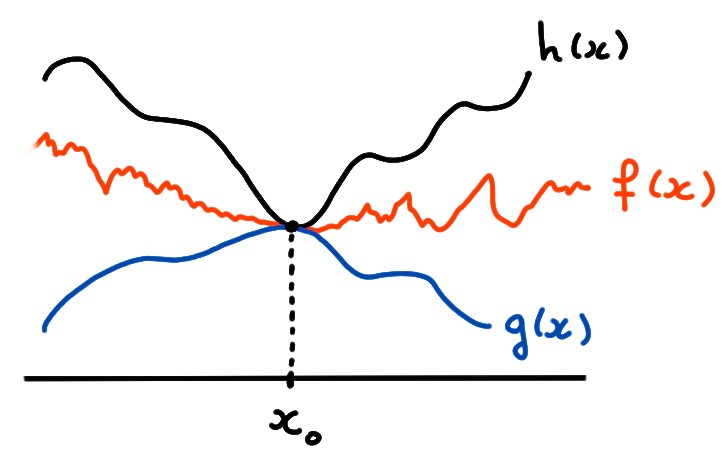
Le résultat suivant est l'analogue de celui vu précédemment pour les suites; il propose de calculer une limite \(x\to x_0\) en comparant \(f(x)\), proche de \(x_0\), à deux fonctions plus simples dont on sait calculer la limite. On formule le résultat pour la limite \(x\to x_0\), mais il peut aussi se formuler pour les limites latérales (section suivante).
Théorème: (Théorème des deux gendarmes) Soit \(f\) définie sur un voisinage \(V\) épointé de \(x_0\). Soient \(g,h\), également définies sur \(V\), telles que
Fixons \(\varepsilon\gt 0\). Puisque \(\lim_{x\to x_0} g(x)=\lim_{x\to x_0} h(x)=L\), il existe un \(\delta\gt 0\) tel que \(|g(x)-L|\leqslant \varepsilon\) et \(|h(x)-L|\leqslant \varepsilon\) pour tout \(0\lt |x-x_0|\leqslant \delta\). Ceci implique que si \(0\lt |x-x_0|\leqslant \delta\), alors \[ f(x)-L\leqslant h(x)-L\leqslant |h(x)-L|\leqslant\varepsilon\,, \] mais aussi \[ f(x)-L\geqslant g(x)-L\geqslant -|g(x)-L|\geqslant-\varepsilon\,. \] Et donc \(|f(x)-L|\leqslant \varepsilon\).
Exemple: Considérons la fonction \[ f(x)= |x|\sin \left(\frac{1}{\sqrt{5|x|}}\right)\,, \] bien définie dans un voisinage épointé de \(x_0=0\). Pour calculer sa limite lorsque \(x\to 0\), on peut remarquer que \(-1\leqslant \sin(\cdots)\leqslant +1\), et donc pour tout \(x\neq 0\), \[\underbrace{-|x|}_{=g(x)}\leqslant f(x)\leqslant \underbrace{|x|}_{=h(x)}\] Comme \(\lim_{x\to 0 }g(x)=\lim_{x\to 0}h(x)=0\), le théorème des deux gendarmes implique que \(\lim_{x\to 0}f(x)=0\).
Dernière compilation: 2024-10-05 (22:34:28)
Sauf indication contraire, le contenu de ce document est soumis à une licence Creative Commons internationale, Attribution: Pas d'Utilisation Commerciale - Partage dans les Mêmes Conditions 4.0 (CC BY-NC-SA 4.0)
