L'idée est de construire deux suites convergentes \((a_n)_{n\geqslant 0}\) et \((b_n)_{n\geqslant 0}\). Celles-ci sont construites par récurrence:

1. Posons \(a_0:= a\), \(b_0:= b\). Par définition, \(f(a_0)\lt h\lt f(b_0)\).
2. Pour \(n\geqslant 0\), supposons que \(a_n\) et \(b_n\) ont déjà été définis, et que \(f(a_n)\leqslant h\leqslant f(b_n)\). Considérons alors le point milieu de \(a_n\) et \(b_n\): \[c_n:= \frac{a_n+b_n}{2}\,. \]
   • Si \(f(c_n)\leqslant h\), on pose \(a_{n+1}:= c_n\), \(b_{n+1}:= b_n\).
   • Si \(f(c_n)\gt h\), on pose \(a_{n+1}:= a_n\), \(b_{n+1}:= c_n\). Par définition de \(a_{n+1}\) et \(b_{n+1}\), \(f(a_{n+1})\leqslant h\leqslant f(b_{n+1})\).

Maintenant que les suites \((a_n)_{n\geqslant 0}\) et \((b_n)_{n\geqslant 0}\) ont été construites, regardons-les de plus près:

• À chaque étape de l'algorithme ci-dessus, \(a_{n+1}\) est soit \(a_n\), soit \(c_n\). Comme \(c_n\gt a_n\), ceci implique que dans tous les cas, \(a_{n+1}\geqslant a_n\). De plus, chaque \(a_n\) est inférieur à \(b\). Par conséquent, \((a_n)_{n\geqslant 0}\) est croissante et majorée, donc elle converge: notons sa limite \[c_-:= \lim_{n\to \infty} a_n\,.\]
• À chaque étape de l'algorithme ci-dessus, \(b_{n+1}\) est soit \(b_n\), soit \(c_n\). Comme \(c_n\lt b_n\), ceci implique que dans tous les cas, \(b_{n+1}\leqslant b_n\). De plus, chaque \(b_n\) est supérieur à \(a\). Par conséquent, \((b_n)_{n\geqslant 0}\) est décroissante et minorée, donc elle converge: notons sa limite \[c_+:= \lim_{n\to \infty} b_n\,.\]
• Comme à chaque étape exactement un des points devient le point milieu, on a \[ |a_{n+1}-b_{n+1}|=\frac12 |a_n-b_n|=\cdots=\frac{1}{2^{n+1}}|a-b|\to 0\,. \] Par l'inégalité triangulaire, on a donc que \[ |c_--c_+|\leqslant |c_--a_n|+|a_n-b_n|+|b_n-c_+| \to 0\,, \] ce qui implique que \(c_-=c_+\), que l'on peut donc écrire simplement \(c\).

On utilise maintenant de manière essentielle la continuité de \(f\):

1. D'une part, comme \(a_n\to c_-\) et \(f(a_n)\leqslant h\) pour tout \(n\), on a que \[ f(c)=f(c_-)=\lim_{n\to \infty} f(a_n)\leqslant h\,. \]
2. D'autre part, comme \(b_n\to c_+\) et \(f(b_n)\geqslant h\) pour tout \(n\), on a que \[ f(c)=f(c_+)=\lim_{n\to \infty} f(b_n)\geqslant h\,. \]

Ceci implique bien que \(f(c)=h\).

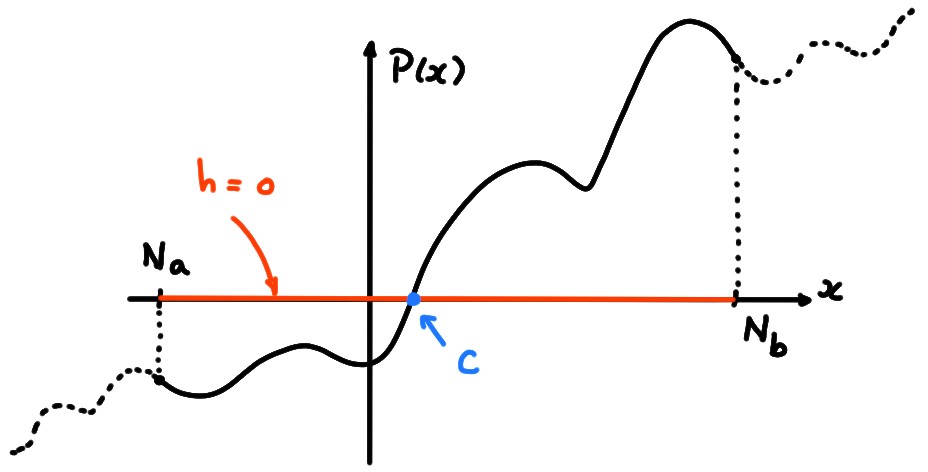
Considérons un polynôme de degré impair, à coefficients réels: \[ P(x)=a_0+a_1x+a_2x^2+\dots a_nx^n\, \] où \(n\) est impair, et \(a_n\neq 0\). Rappelons que ce polynôme est une fonction continue de la variable \(x\).

Sans perte de généralité, supposons que \(a_n\gt 0\). Comme \(n\) est impair, on a \[ \lim_{x\to+\infty}P(x)=+\infty\,,\qquad \lim_{x\to-\infty}P(x)=-\infty\,. \] Il existe donc un réel \(N_a\lt 0\) tel que \(P(N_a)\lt 0\), et un réel \(N_b\gt 0\) tel que \(P(N_b)\gt 0\).

En appliquant le Théorème de la valeur intermédiaire sur l'intervalle \([N_a,N_b]\), avec \(h=0\), on conclut: il existe \(c\in ]N_a,N_b[\) tel que \(P(c)=0\).

On sait que \(f\) atteint son minimum et son maximum: \[ f(x^*)=\max_{x\in [a,b]}f(x)\,,\qquad f(x_*)=\min_{x\in [a,b]}f(x)\,. \] Puisque \(f(x_*)\leqslant f(x)\leqslant f(x^*)\) pour tout \(x\in [a,b]\), on a \[\mathrm{Im} (f)\subset [f(x_*),f(x^*)]\,.\] Si \(x_*=x^*\), alors \(f\) est constante et donc \(\mathrm{Im} (f)\) ne contient qu'un point (qu'on peut considérer comme un intervalle fermé et borné). Sinon, on peut supposer sans perte de généralité que \(x_*\lt x^*\).

En choisissant un \(h\in [f(x_*),f(x^*)]\) quelconque, le théorème de la valeur intermédiaire garantit qu'il existe un \(c\in ]x_*,x^*[\) tel que \(f(c)=h\). Par conséquent, \(h\in \mathrm{Im} (f)\), et donc \[[f(x_*),f(x^*)] \subset \mathrm{Im} (f)\,.\] On a donc montré que \(\mathrm{Im} (f)=[f(x_*),f(x^*)]\), qui est bien un intervalle fermé et borné.