Une fonction continue définie sur un intervalle compact, c'est-à-dire fermé et borné (donc du type \([a,b]\)), possède plusieurs propriétés remarquables. Commençons par définir ce que signifie être continue sur un intervalle fermé et borné:
Une première propriété importante est qu'une fonction continue sur un compact ne peut pas prendre de valeurs arbitrairement grandes:
Théorème: Soit \(f:[a,b]\to \mathbb{R}\) continue. Alors \(f\) est bornée.
Par l'absurde,
supposons que \(f\) n'est pas majorée.
Alors pour tout \(n\gt 0\) il existe
\(x_n\in [a,b]\) tel que \(f(x_n)\gt n\), et donc \(f(x_n)\to +\infty\).
Par construction, \((x_n)_n\) est bornée.
Par le Théorème de
Bolzano-Weierstrass, il existe une sous-suite \((x_{n_k})_k\)
et \(x^*\in [a,b]\)
telle que \(\lim_{k\to\infty}x_{n_k}= x^*\). Mais donc, puisque \(f\) est
continue, elle est en particulier continue en \(x^*\), et donc
\[
f(x^*)=\lim_{k\to\infty}f(x_{n_k})=\lim_{n\to \infty} f(x_n)=+\infty\,,
\]
ce qui est impossible (puisque \(f(x^*)\) doit être un nombre fini!).
Donc \(f\) est majorée.
En adaptant l'argument, on montre que \(f\) est minorée.
Une deuxième propriété, très utile dans les problèmes d'optimisation: si une fonction est continue sur un compact, elle atteint toujours son minimum et son maximum:
Théorème: Soit \(f:[a,b]\to \mathbb{R}\) continue. Alors \(f\) atteint son minimum et son maximum: il existe \(x_*\) et \(x^*\in[a,b]\) tels que \[ \min_{x\in [a,b]}f(x)=f(x_*)\,,\qquad \max_{x\in [a,b]}f(x)=f(x^*)\,. \]
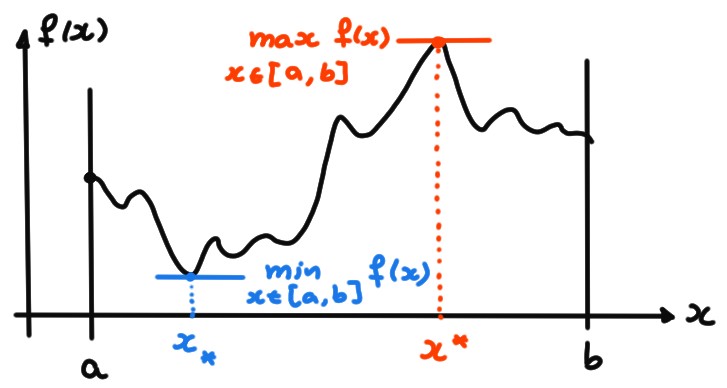
Par le théorème précédent, \(f\) est bornée, et donc
\[
s:= \sup_{x\in [a,b]}f(x)
\]
est bien défini. Nous allons montrer qu'il existe un point \(x^*\in [a,b]\) où
\(f\) prend cette valeur \(s\).
Considérons la suite \(\varepsilon_n:= \frac1n\).
Par définition du supremum, pour tout \(n\) il existe \(x_n\in [a,b]\) tel que
\[
s-\varepsilon_n\leqslant f(x_n)\leqslant s\,.
\]
Par construction, \(f(x_n)\to s\) lorsque \(n\to\infty\).
Mais, comme \((x_n)_n\) est bornée (elle vit dans \([a,b]\)!),
le Théorème de
Bolzano-Weierstrass garantit qu'il existe une
sous suite \((x_{n_k})_k\), et un \(x^*\in [a,b]\),
tels que \(\lim_{k\to\infty}x_{n_k}=x^*\).
Calculons \(f(x^*)\). Puisque \(f\) est continue sur \([a,b]\), elle est en
particulier continue en \(x^*\). Comme \(x_{n_k}\to x^*\), on a donc
\[
f(x^*)=\lim_{k\to\infty}f(x_{n_k})\,.
\]
Mais, puisque \((f(x_{n_k}))_k\) est une sous-suite de \((f(x_n))_n\), elle
converge vers la même limite:
\[
f(x^*)=\lim_{k\to\infty}f(x_{n_k})
=\lim_{n\to\infty}f(x_n)=s\,.
\]
On a donc
\[ f(x^*)
=\sup_{x\in [a,b]}f(x)
=\max_{x\in [a,b]}f(x)\,.
\]
On procède de même pour la construction d'un point \(x_*\) où \(f\) atteint son
minimum.
Exemple: Considérons \(f:[0,2]\to \mathbb{R}\), définie par \[ f(x)=x^3\sin(x^2+\cos(x))\,. \] Cette fonction est continue (c'est un produit de \(x^3\) avec une composée de fonctions continues), donc par le théorème, il existe \(x_*\in [0,2]\) et \(x^*\in [0,2]\) tels que \[ f(x_*)=\min_{x\in [0,2]}f(x)\,,\qquad f(x^*)=\max_{x\in [0,2]}f(x)\,. \]
Pour souligner l'importance des hypothèses dans le théorème ci-dessus, voyons comme le résultat n'est plus vrai en général lorsqu'une des hypothèses n'est pas vérifiée:
Exemple: (Une fonction sur un intervalle compact, mais qui n'est pas continue en un point.) Soit \(f:[0,1]\to \mathbb{R}\) définie par \[ f(x):= \begin{cases} x&\text{ si }0\leqslant x\lt \frac12\,,\\ 0&\text{ si } x=\frac12\,,\\ x-1&\text{ si } \frac12\lt x\leqslant 1\,.\\ \end{cases} \] Cette fonction est continue partout sauf en \(\frac12\), et elle ne possède ni de maximum ni de minimum:
Exemple: (Une fonction continue, sur un intervalle borné mais pas fermé.) Considérons \[f(x)=\frac{1}{1-x^2}\,,\qquad \text{sur } ]-1,1[\,.\] Alors \(f\) possède un minimum, atteint en \(x_*=0\), mais pas de maximum:
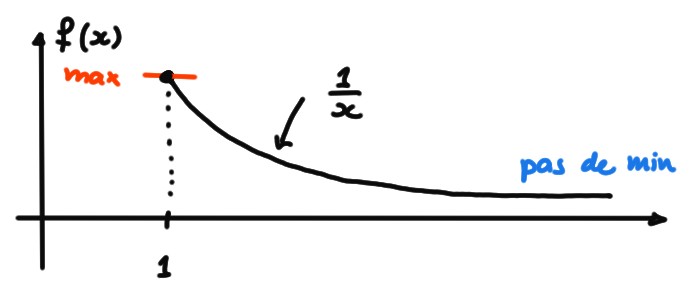
Exemple: (Une fonction continue sur un intervalle fermé mais pas borné.) Soit \[f(x)=\frac{1}{x}\,,\qquad \text{ sur } [1,+\infty[\,.\] Alors \(f\) possède un maximum, atteint sur le bord en \(x^*=1\), mais pas de minimum:
Dernière compilation: 2024-12-04 (07:30:07)
Sauf indication contraire, le contenu de ce document est soumis à une licence Creative Commons internationale, Attribution: Pas d'Utilisation Commerciale - Partage dans les Mêmes Conditions 4.0 (CC BY-NC-SA 4.0)
