Analyse 1 | S. Friedli (EPFL)

8.2 Prolongement par continuité

Supposons qu'une fonction ait un ''trou'' dans son domaine, au point \(x_0\). Si l'on veut étendre le domaine de cette fonction, de façon à ce que son domaine contienne aussi \(x_0\), comment doit-on définir \(f(x_0)\)?

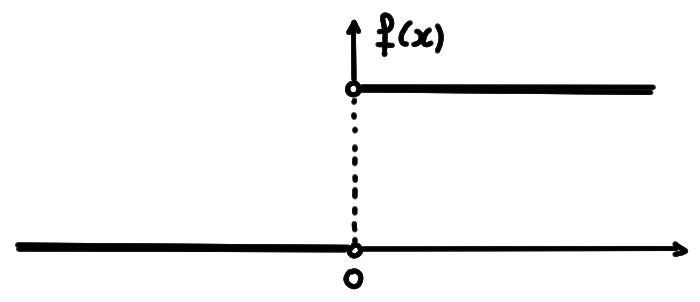
Soit \(I\) un intervalle, \(x_0\in I\), et soit \(I':= I\setminus\{x_0\}\). On obtient donc \(I\) en rajoutant à \(I'\) le point \(x_0\).

Soit maintenant une fonction \(f:I'\to\mathbb{R}\), c'est-à-dire définie sur \(I\) à l'exception du point \(x_0\).

Si on veut étendre le domaine de \(f\) à tout \(I\), il faut choisir une valeur pour \(f(x_0)\). Ce choix est a priori arbitraire, mais une façon naturelle de le faire est de donner à \(f\), au point \(x_0\), une valeur qui est semblable à celles qu'elle prend dans le voisinage de \(x_0\).

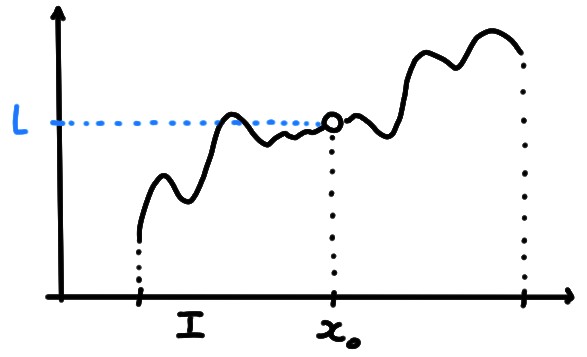
Plus précisément: si le nombre \[ L= \lim_{x\to x_0}f(x) \] existe, il est naturel de l'utiliser pour définir la valeur de \(f\) au point \(x_0\): \[ f(x_0):= L\,. \] Cette procédure est surtout utilisée dans le cas où \(f\) est, au départ, continue en tout point de \(I'\):

Si la limite \(L\) existe, la nouvelle fonction \[\begin{aligned} \widetilde{f}:I&\to \mathbb{R}\\ x&\mapsto \begin{cases} f(x)&\text{ si }x\neq x_0\,,\\ L&\text{ si }x=x_0\,. \end{cases} \end{aligned}\] est continue en tout point de \(I\); elle s'appelle la prolongée de \(f\) par continuité:

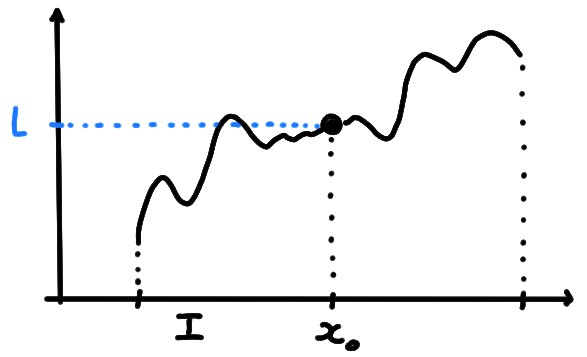
Du point de vue du graphe, on est parti d'une fonction qui était déjà continue en tous les points de \(I'\), et l'existence de \(L\) a permis de simplement ''boucher le trou'', pour rendre la fonction continue sur tout \(I\).

Exemple: Considérons la fonction \(f:\mathbb{R}\setminus\{3\}\to \mathbb{R}\), définie par \[ f(x):= \begin{cases} \sqrt{4-x}&\text{ si }x\lt 3\,,\\ x-2&\text{ si }x\gt 3\,. \end{cases} \] On a montré précédemment que \(f\) est continue en tout point \(x\neq 3\). On a aussi calculé \[ \lim_{x\to 3}f(x)=1\,. \] On peut donc prolonger cette fonction par continuité à tout \(\mathbb{R}\), en définissant \[ \widetilde{f}(x):= \begin{cases} \sqrt{4-x}&\text{ si }x\lt 3\,,\\ 1&\text{ si }x=3\,,\\ x-2&\text{ si }x\gt 3\,. \end{cases} \]

Exemple: Considérons \(f:\mathbb{R}^*\to\mathbb{R}\), définie par \[f(x):=\frac{\sin (x)}{x}\,.\]

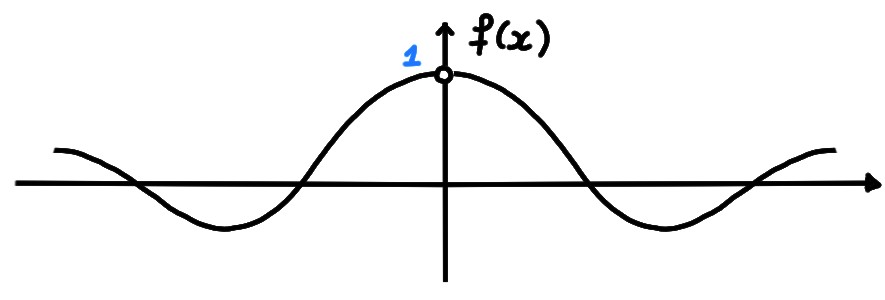
Clairement, \(f\) est continue en tout point \(x_0\in \mathbb{R}^*\). On sait que \[ \lim_{x\to 0}f(x)= \lim_{x\to 0}\frac{\sin(x)}{x}=1\,, \] donc \(f\) peut être prolongée par continuité à tout \(\mathbb{R}\). Sa prolongée est donnée par \[ \widetilde{f}(x)= \begin{cases} \frac{\sin(x)}{x}&\text{ si }x\neq 0\,,\\ 1&\text{ si }x=0\,. \end{cases} \]

On ne peut pas toujours, comme dans les deux exemples précédents, ''boucher le trou'' pour rendre une fonction continue partout:

Exemple: Soit \(f:\mathbb{R}^*\to\mathbb{R}\) définie par \[ f(x):= \begin{cases} 0&\text{ si }x\lt 0\,,\\ 1&\text{ si }x\gt 0\,. \end{cases} \]

Alors \(f\) est continue en tout point de \(\mathbb{R}_*\), Mais comme \(\lim_{x\to 0}f(x)\) n'existe pas (puisque \(\lim_{x\to 0^-}f(x)=0\) est différent de \(\lim_{x\to 0^+}f(x)=1\)), cette fonction ne peut pas être prolongée par continuité.

Quiz 8.2-1 : Soit \(x_0\in ]-1,1[\) et soit \(f\) une fonction continue en chaque point de \(]-1,1[\setminus\{x_0\}\). Vrai ou faux?

\(f\) est continue en \(x_0\).
La limite \(\lim_{x\to x_0}f(x)\) existe.
Au moins une des limites latérales \(\lim_{x\to x_0^{\pm}}f(x)\) existe.
Il existe une prolongée par continuité \(\widetilde{f}:]-1,1[\to \mathbb{R}\).
Si \(\lim_{x\to x_0}f(x)\) existe, alors la fonction \(g:\mathbb{R}\setminus\{x_0\} \to \mathbb{R}\), définie par \(g(x):=\frac{f(x)}{f(x)^2+1}\) pour tout \(x\neq x_0\), est prolongeable par continuité en \(x_0\).