Analyse 1 | S. Friedli (EPFL)

8.5 Continuité et calcul de limites

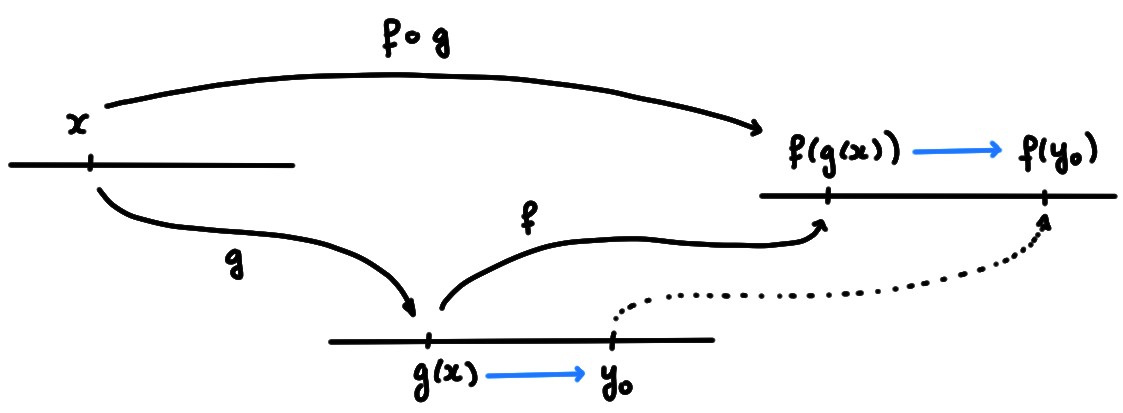
On a déjà vu que si une fonction \(f\) est continue en un point \(x_*\), alors pour toute suite \((x_n)\) tendant vers \(x_*\), \[ \lim_{n\to \infty} f(x_n)=f\bigl(\lim_{n\to\infty}x_n\bigr)=f(x_*). \] Voyons maintenant un résultat analogue, mais dans lequel la suite \(x_n\) (dont la variable est l'entier \(n\)) est remplacée par une fonction \(g(x)\) (dont la variable est un réel \(x\)):

Théorème: Soit \(f(y)\) définie dans le voisinage d'un point \(y_0=L\), et continue en ce point \(y_0\).

Si \(g\) est définie dans un voisinage de \(x_0\), et si \(\displaystyle\lim_{x\to x_0}g(x)=y_0\), alors \[\lim_{x\to x_0}f(g(x))=f(y_0)\,.\]
Si \(g\) est définie sur un domaine contenant un intervalle de la forme \(]a,+\infty[\), et si \(\displaystyle\lim_{x\to \infty}g(x)=y_0\), alors \[\lim_{x\to \infty}f(g(x))=f(y_0)\,.\]

Preuve:

On démontre la première affirmation.

Fixons \(\varepsilon\gt 0\). On procède en deux étapes:

Puisque \(f\) est continue en \(y_0\), il existe \(\eta\gt 0\) tel que \(|f(y)-f(y_0)|\leqslant \varepsilon\) dès que \(0\lt |y-y_0|\leqslant \eta\).
Ensuite, puisque \(\lim_{x\to x_0}g(x)=y_0\), il existe \(\delta\gt 0\) tel que \(|g(x)-y_0|\leqslant \eta\) dès que \(0\lt |x-x_0|\leqslant \delta\).

Prenons donc un \(x\) tel que \(0\lt |x-x_0|\leqslant \delta\). En utilisant la première étape avec \(y=g(x)\), on a \[ |f(g(x))-f(y_0)| =|f(y)-f(y_0)| \leqslant \varepsilon\,. \] Ceci montre bien que \(\lim_{x\to x_0}f(g(x))=f(y_0)\).

La deuxième affirmation se démontre de la même façon.

En d'autres termes, lorsqu'on étudie une limite d'une composée \(f(g(x))\), dans laquelle on sait que \(g(x)\to y_0\), et que \(f\) est continue au point \(y_0\), alors on peut ''rentrer la limite dans \(f\)'': \[ \lim f(g(x))=f\bigl(\lim g(x)\bigr)=f(y_0)\,. \]

Exemple: Considérons la limite \[ \lim_{x\to\infty}\sqrt{\frac{x}{x+1}}\,. \] On voit ici que \(g(x)=\frac{x}{x+1}\to 1\) lorsque \(x\to \infty\). Montrons que \(f(x)=\sqrt{x}\) est continue en \(y_0=1\). En effet, puisque \[\begin{aligned} |f(x)-f(1)|= |\sqrt{x}-\sqrt{1}|= \frac{|x-1|}{\sqrt{x}+1}\leqslant |x-1|\,, \end{aligned}\] on a bien que \(\lim_{x\to 1}f(x)=f(1)\).

On peut donc ''rentrer la limite dans \(f\)'' \[ \lim_{x\to\infty}\sqrt{\frac{x}{x+1}}= \sqrt{\lim_{x\to\infty}\frac{x}{x+1}}=\sqrt{1}=1\,. \]