9.9 Extréma locaux et le Théorème de Rolle
Soit \(f\) définie en \(x_0\) et dans son voisinage. On dit que

Bien-sûr, un maximum/minimum global est aussi local.

Le point de départ de cette section est le résultat suivant. Il suggère que la dérivée peut s'avérer être un outil pour la recherche de minimums/maximums:

Lemme: Soit \(f\) définie en \(x_0\) et dans son voisinage. Si \(f\) possède un minimum/maximum local en \(x_0\), et si \(f\) est dérivable en \(x_0\), alors \[f'(x_0)=0\,.\]

Supposons que \(f\) possède un maximum local en \(x_0\): \(\exists \delta\gt 0\) tel que \(f(x)\leqslant f(x_0)\) pour tout \(x\in I:= ]x_0-\delta,x_0+\delta[\).

  • Si \(x\in I\), \(x\gt x_0\), on a toujours \(f(x)-f(x_0)\leqslant 0\) puisque \(x_0\) est un maximum local, et donc aussi (puisque \(x-x_0\gt 0\)) \[\frac{f(x)-f(x_0)}{x-x_0}\leqslant 0 \]
    En prenant \(x\to x_0^+\), cela donne \[ f'(x_0)=\lim_{x\to x_0^+} \frac{f(x)-f(x_0)}{x-x_0}\leqslant 0\,. \]
  • En procédant de même pour un \(x\lt x_0\), on \[\frac{f(x)-f(x_0)}{x-x_0}\geqslant 0\,, \] et donc en prenant \(x\to x_0^-\), on montre que \(f'(x_0)\geqslant 0\).
Puisque \(f\) est dérivable en \(x_0\), on doit avoir \(f'(x_0)=f'_+(x_0)=f'_-(x_0)\), et puisque ce nombre est à la fois \(\leqslant 0\) et \(\geqslant 0\), on a \(f'(x_0)=0\).

Remarque: L'affirmation contraire n'est pas vraie: si \(f\) est dérivable en \(x_0\) et si \(f'(x_0)=0\), cela n'implique pas que \(f\) possède un minimum ou un maximum local en \(x_0\)! Prendre par exemple \(f(x)=x^3\) au point \(x_0=0\):

Comme \(f'(x)=3x^2\), on a \(f'(0)=0\), bien que \(0\) ne soit ni un minimum ni un maximum local.

Théorème:[Théorème de Rolle] Soit \(f:[a,b]\to \mathbb{R}\) continue, dérivable sur \(]a,b[\). Si \(f(a)=f(b)\), alors il existe \(c\in ]a,b[\) tel que \[f'(c)=0\,.\]

Si \(f\) est constante, \(f(a)=f(x)=f(b)\) pour tout \(x\in ]a,b[\), sa dérivée est nulle et donc on peut prendre n'importe quel point \(c\in]a,b[\), et avoir \(f'(c)=0\).

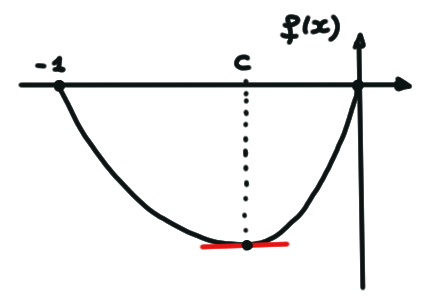
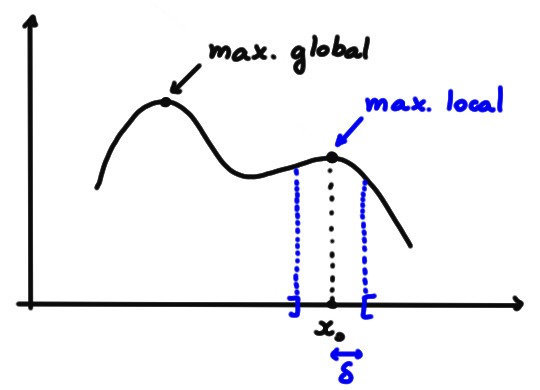
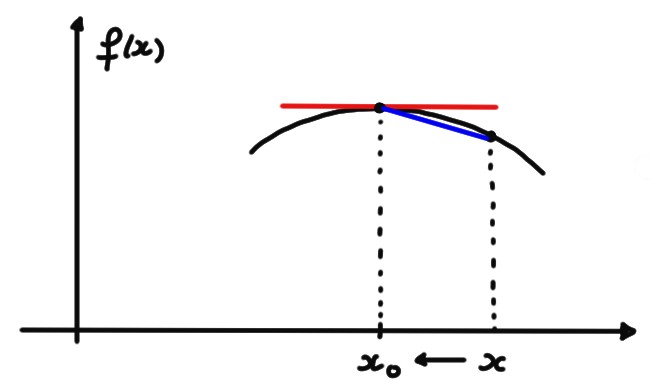
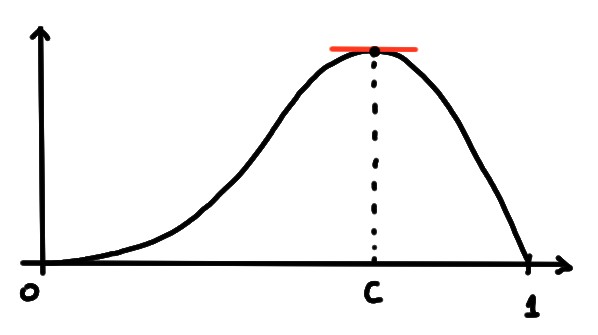
Supposons donc que \(f\) n'est pas constante. Comme \(f\) est continue sur l'intervalle compacte \([a,b]\), elle atteint son maximum en un point \(x^*\in [a,b]\), et son minimum en un point \(x_*\in [a,b]\). Comme \(f\) n'est pas constante, au moins un de ces points se trouve strictement à l'intérieur de l'intervalle. Supposons que c'est \(x^*\in ]a,b[\). Comme \(x^*\) est un maximum global, c'est aussi un maximum local, et par le lemme précédent \(f'(x^*)=0\).

L'interprétation géométrique du Théorème de Rolle est claire: si le graphe d'une fonction lisse (continue et dérivable) part d'un point \(A=(a,f(a))\) et arrive en un point \(B=(b,f(b))\) qui est à la même hauteur que \(A\), alors il existe au moins un point de son graphe où la droite tangente est horizontale:

Exemple: Soit \(f:[0,1]\to\mathbb{R}\), définie par \[ f(x):= \sin (\pi x^2)\cos(x)\,. \] Comme \(f\) est continue et dérivable, et comme \(f(0)=f(1)=0\), il existe \(c\in ]0,1[\) tel que \(f'(c)=0\).

Dans ce cas, \(c\) est solution de l'équation non-linéaire \[2\pi c\cos(\pi c^2)\cos(c)-\sin(\pi c^2)\sin(c)=0\,, \] et ne peut pas être donné explicitement.

Parfois, le point \(c\) peut se calculer explicitement:

Exemple: Soit \(f:[-1,0]\to \mathbb{R}\) définie par \[ f(x):= x^4+x\,. \] On a \(f(-1)=f(0)=0\), et donc par le Théorème de Rolle il existe \(c\in ]-1,0[\) tel que \(f'(c)=0\).

De plus, comme \(f'(x)=4x^3+1\), on a \[ f'(c)=0\,\Longleftrightarrow\, 4c^3+1=0\,\Longleftrightarrow\, c=-\sqrt[3]{\frac14}\,. \]

Bien-sûr, si une des conditions du théorème n'est pas vérifiée, la conclusion du théorème n'est plus garantie (en général).

Exemple: Soit \(f:[0,2]\to \mathbb{R}\), définie par \[ f(x):=|x-1|\,. \] Ici \(f(0)=f(2)=1\), mais il n'existe aucun \(c\in ]0,2[\) tel que \(f'(c)=0\).

Ce n'est pas une contradiction avec le Théorème de Rolle, puisque \(f\) ne satisfait pas aux hypothèses: elle est continue sur \([0,2]\), dérivable en tout point de \(]0,2[\) sauf en \(x=1\).

Quiz 9.9-1 : Soit \(f\) définie en \(x_0\) et dans son voisinage. Vrai ou faux?
  1. Si \(x_0\) est à la fois un minimum et un maximum local, alors \(f\) est constante dans un petit intervalle autour de \(x_0\).
  2. Si \(x_0\) est un maximum ou un minimum local, alors \(f\) est dérivable en \(x_0\).
  3. Si \(f\) possède un minimum local en \(x_0\), alors \(f\) est continue en \(x_0\).
  4. Si \(f\) n'est pas dérivable en \(x_0\), alors \(x_0\) n'est ni un minimum, ni un maximum local.
  5. Si \(f\) possède un maximum local en \(x_0\), alors \(f(x)\leqslant f(x_0)\) pour tout \(x\).
  6. ⚡ Si \(f\) est dérivable partout et si \(x_0\) est un minimum local stricte, alors \(f'(x_0)=0\), et il existe \(\delta\gt 0\) tel que \(f'(x)\neq 0\) pour tout \(x\in ]x_0-\delta,x_0[\cup]x_0,x_0+\delta[\).
Quiz 9.9-2 : Parmi ces affirmations, lesquelles sont toujours vraies?
  1. Soit \(f:[a,b]\to\mathbb{R}\) continue. Si il existe un point \(c\in ]a,b[\) où \(f\) est dérivable et \(f'(c)=0\), alors \(f\) est dérivable sur \(]a,b[\).
  2. Soit \(f:[a,b]\to \mathbb{R}\) continue sur \(]a,b[\), dérivable sur \(]a,b[\), telle que \(f(a)=f(b)\). Alors il existe \(c\in ]a,b[\) tel que \(f'(c)=0\).
  3. Soit \(f:[a,b]\to \mathbb{R}\) continue sur \(]a,b[\), dérivable sur \(]a,b[\), telle que \(f(a)>f(b)\). Alors il existe \(c\in ]a,b[\) tel que \(f'(c)<0\).
  4. Soit \(f:[a,b]\to \mathbb{R}\) continue sur \([a,b]\), dérivable sur \(]a,b[\), et telle qu'il existe \(c\in ]a,b[\) tel que \(f'(c)>0\). Alors \(f(a)< f(b)\).
  5. Soit \(f:[a,b]\to \mathbb{R}\) continue sur \(]a,b[\), dérivable sur \(]a,b[\), telle que \(\lim_{x\to a^+}f(x)=\lim_{x\to b^-}f(x)\). Alors il existe \(c\in ]a,b[\) tel que \(f'(c)=0\).
  6. ⚡ Soit \(f:[a,b]\to \mathbb{R}\) continue sur \([a,b]\), telle que \(f(a)=f(b)\). Alors il existe au moins un point \(c\in ]a,b[\) où \(f\) est dérivable.
  7. Soit \(f:\mathbb{R}\to \mathbb{R}\) dérivable en tout point \(x_0\in [a,b]\), telle que \(f(a)=f(b)\). Alors il existe \(c\in ]a,b[\) tel que \(f'(c)=0\).
Quiz 9.9-3 : (MAN 2021) Vrai ou faux? Si \(f(x)=e^{x(x-1)(x-\pi)}+e^{\sin^2(x)}\), alors il existe \(x\in ]0,\pi[\) tel que \(f'(x)=0\).
  1. FAUX
  2. VRAI

Dernière compilation: 2024-12-04 (07:30:07)

Sauf indication contraire, le contenu de ce document est soumis à une licence Creative Commons internationale, Attribution: Pas d'Utilisation Commerciale - Partage dans les Mêmes Conditions 4.0 (CC BY-NC-SA 4.0)