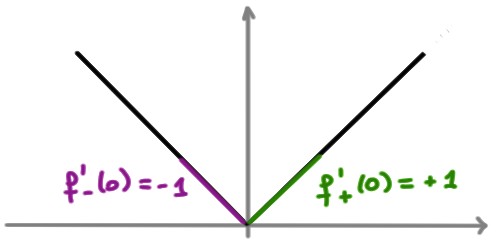
Exemple: On sait que \(f(x)=|x|\) n'est pas dérivable en \(x_0=0\):
Pour parler de la dérivabilité d'une fonction en un point \(x_0\), il
faut que cette fonction soit définie dans un voisinage épointé de
\(x_0\). Ceci signifie en particulier que \(f\) doit être définie
des deux côtés de \(x_0\).
Si \(f\) n'est définie que d'un côté de \(x_0\),
on peut tout de même introduire une notion de dérivée latérale:
Observons que la dérivabilité à gauche (resp. à droite) en \(x_0\) implique qu'il existe une droite tangente à gauche (resp. à droite) au point \((x_0,f(x_0))\).
Il peut donc exister des fonctions qui peuvent être dérivables à gauche ou à droite en un point, mais sans être dérivable en ce point.
Exemple: On sait que \(f(x)=|x|\) n'est pas dérivable en \(x_0=0\):

L'existence et l'égalité des dérivées latérales en un point entraîne la dérivabilité en ce point:
Théorème: \(f\) est dérivable en \(x_0\) si et seulement si \(f'_-(x_0)\) et \(f'_+(x_0)\) existent et sont égales (et dans ce cas, \(f'(x_0)=f'_-(x_0)=f'_+(x_0)\)).
Par définition, \[\begin{aligned} f'_-(x_0)&=\lim_{x\to x_0^-} \frac{f(x)-f(x_0)}{x-x_0}\,,\\ f'_+(x_0)&=\lim_{x\to x_0^-} \frac{f(x)-f(x_0)}{x-x_0}\,. \end{aligned}\] Donc ces deux limites existent et sont égales si et seulement si \[ \lim_{x\to x_0} \frac{f(x)-f(x_0)}{x-x_0} \] existe et prend la même valeur.
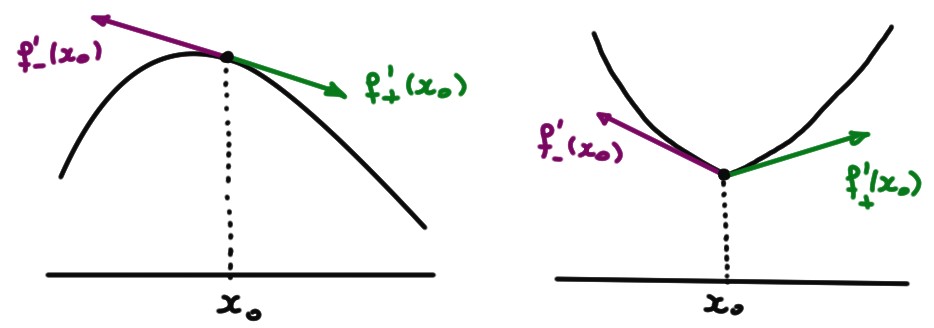
Soient \(f,g\) deux fonctions définies sur toute la droite, et \(x_*\in \mathbb{R}\). Considérons la fonction \(f\) suivante, définie par morceaux: \[ f(x):= \begin{cases} g(x)&\text{ si }x\leqslant x_*\,,\\ h(x)&\text{ si }x> x_*\,. \end{cases} \] Si \(f\) est continue en \(x_*\), on pourra tester la dérivabilité de \(f\) en \(x_*\), par le théorème précédent, en calculant les dérivées latérales de \(f\) en \(x_*\), et en vérifiant qu'elle sont égales.
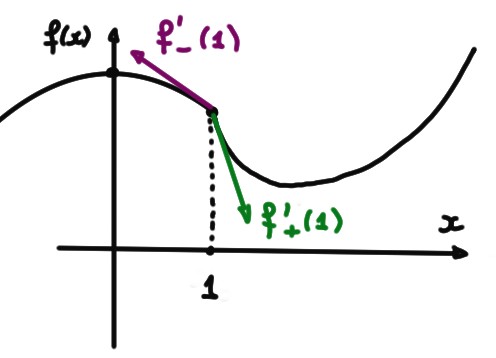
Exemple:
Étudions la dérivabilité de
\[
f(x)=
\begin{cases}
g(x)=3-x^2&\text{ si }x\leqslant 1\,,\\
h(x)=x^3-3x^2+4&\text{ si }x>1\,
\end{cases}
\]
au point \(x_*=1\).
Remarquons que \(f\) est continue en ce point puisque
\[
\lim_{x\to 1^-}f(x)=
\lim_{x\to 1^-}g(x)=2=
\lim_{x\to 1^+}h(x)=
\lim_{x\to 1^+}f(x)\,,
\]
qui est également égale à \(f(1)=2\).
Pour tester la dérivabilité,
\[\begin{aligned} f'_-(1)
&=\lim_{x\to 1^-}\frac{f(x)-f(1)}{x-1}\\
&=\lim_{x\to 1^-}\frac{g(x)-g(1)}{x-1}\\
&=\lim_{x\to 1^-}\frac{(3-x^2)-2}{x-1}
=-2
\end{aligned}\]
\[\begin{aligned} f'_+(1)
&=\lim_{x\to 1^+}\frac{f(x)-f(1)}{x-1}\\
&=\lim_{x\to 1^+}\frac{h(x)-g(1)}{x-1}\\
&=\lim_{x\to 1^+}\frac{(x^3-3x^2+4)-2}{x-1}
=-3
\end{aligned}\]
Comme \(f'_-(1)\neq f'_+(1)\), \(f\) n'est pas dérivable en \(1\).
Exemple:
Soit
\[f(x):=
\begin{cases}
x^2+a x+1&\text{ si }x\lt 0\,,\\
\sin(2x)+b&\text{ si }x\geqslant 0\,.
\end{cases}
\]
Remarquons qu'en dehors de \(0\), \(f\) est partout dérivable, quelles que
soient les valeurs de \(a\) et \(b\).
Déterminons les paramètres
\(a,b\) de manière à ce que \(f\) soit
dérivable en \(x_0=0\).
Pour être dérivable en \(0\), il faut d'abord que \(f\) soit continue en
\(0\). Commençons donc par assurer que \(f\) est continue en \(0\).
Pour cela, remarquons que \(f(0)=\sin(2\cdot 0)+b=b\),
\[
\lim_{x\to 0^+}f(x)
=\lim_{x\to 0^+}(\sin(2x)+b)
=b\,,
\]
et
\[
\lim_{x\to 0^-}f(x)=\lim_{x\to 0^-}(x^2+ax+1)=1\,.
\]
Pour avoir la continuité en \(0\), on doit donc imposer \(b=1\).
Passons à la dérivabilité en \(0\).
Puisqu'on peut dorénavant considérer que \(b=1\), on calcule d'abord
\[\begin{aligned}
f'_-(0)&=
\lim_{h\to 0^-}\frac{f(h)-f(0)}{h}\\
&= \lim_{h\to 0^-}\frac{(h^2+ah+1)-1}{h}\\
&= \lim_{h\to 0^-}(a+h)=a\,,
\end{aligned}\]
puis
\[\begin{aligned}
f'_+(0)
&= \lim_{h\to 0^+}\frac{f(h)-f(0)}{h}\\
&= \lim_{h\to 0^+}\frac{(\sin(2h)+1)-1}{h}
\lim_{h\to 0^+}\frac{\sin(2h)}{h}=
2\,.
\end{aligned}\]
Comme \(f\) est dérivable en \(0\) si et seulement si \(f'_-(0)=f'_+(0)\),
la seule possibilité est d'imposer \(a=2\).