Analyse 1 | S. Friedli (EPFL)

9.1 Définition de la dérivée, exemples

00:00

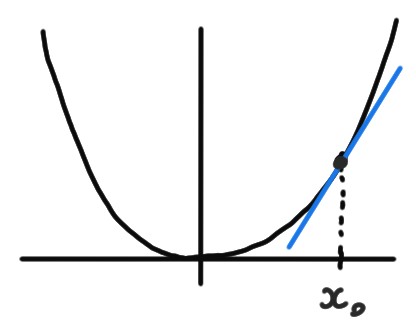
Une question géométrique naturelle, et très utile pour l'étude d'une fonction, est de savoir comment calculer l'équation de la droite tangente au graphe d'une fonction, en un point $(x_0,f(x_0))$ :

0,0

x_0

f(x_0)

\text{Voir la sécante}

x

f(x)

A

\text{Pente de la tangente: }1.2495

\text{Pente de la sécante: }1.5450

Pour connaître l'équation de cette droite, de la forme $y=mx+h\,,$ on commence par chercher sa pente $m$ . Et quand on cherche la pente d'une droite, on a besoin de deux points sur cette droite et ici, on n'en a qu'un, à savoir le point $(x_0,f(x_0))$ .

L'idée est de passer par un processus de limite. En effet, introduisons un deuxième point sur le graphe, $(x,f(x))$ , où $x$ est un point différent de $x_0$ , et considérons la sécante passant par les points $(x_0,f(x_0))$ et $(x,f(x))$ . La pente de cette sécante est donnée par $\frac{f(x)-f(x_0)}{x-x_0}\,.$ Lorsque $x$ est proche de $x_0$ , cette pente approxime celle de la droite que l'on cherche, $m$ . Dans la limite $x\to x_0$ (tester sur l'animation ci-dessus), elle devrait même tendre exactement vers $m$ : $\lim_{x\to x_0}\frac{f(x)-f(x_0)}{x-x_0}=m\,.$ L'existence de la limite ci-dessus n'est pas garantie en générale.

Soit

f

définie en

x_0\in \mathbb{R}

et dans son voisinage. On dit que

f

est dérivable en $x_0$ si le nombre

f'(x_0)

défini par la limite

f'(x_0)=\lim_{x\to x_0}\frac{f(x)-f(x_0)}{x-x_0}

existe (et est fini). On appelle

f'(x_0)

la dérivée (ou nombre dérivé) de $f$ au point $x_0$ .

Remarque: Dans la limite qui définit $f'(x_0)$ , ci-dessus, la variable $x$ est utilisée uniquement pour calculer la limite; on dit qu'elle est muette. On donc peut écrire $f'(x_0)$ de différentes manières: $\begin{aligned} f'(x_0) &=\lim_{x\to x_0}\frac{f(x)-f(x_0)}{x-x_0}\\ &=\lim_{z\to x_0}\frac{f(z)-f(x_0)}{z-x_0}\\ &=\lim_{h\to 0}\frac{f(x_0+h)-f(x_0)}{h}\,, \end{aligned}$ où, dans la dernière égalité, on a fait le changement de variable $h:= z-x_0$ .

Exemple: Soit $f(x)=x^2$ . Au point $x_0=1$ , $f'(1)=\lim_{h\to 0}\frac{f(1+h)-f(1)}{h} =\lim_{h\to 0}\frac{(1+h)^2-1^2}{h}=2\,.$

Donc la tangente à la parabole au point d'abscisse

x_0=1

a une pente de

2

. Son équation est donc de la forme

y=2x+b

, et comme elle doit passer par le point

(1,f(1))=(1,1)

, on trouve

b=-1

. Donc la tangente au point

(1,1)

a pour équation

y=2x-1

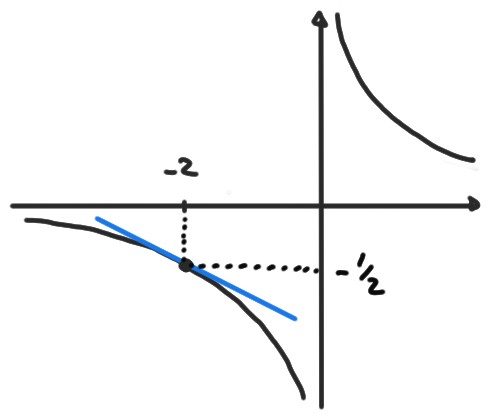
Exemple: Soit $f(x)=\frac{1}{x}$ . Au point $x_0=-2$ , $f'(-2) =\lim_{x\to -2}\frac{f(x)-f(-2)}{x-(-2)} =\lim_{x\to -2}\frac{\frac{1}{x}-\frac{1}{-2}}{x+2} =-\frac14\,.$

Origines possibles de la non-dérivabilité en un point

Voyons quelques exemples de fonctions qui ne sont pas dérivables.

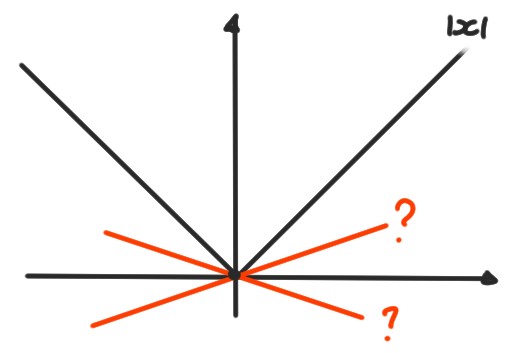
Exemple: Considérons $f(x)=|x|$ . Au point $x_0=0$ , la dérivée s'obtient en prenant la limite $x\to 0$ du rapport $\frac{f(x)-f(0)}{x-0}=\frac{|x|}{x}= \begin{cases} -1&\text{ si }x<0\,,\\ +1&\text{ si }x>0\,.\\ \end{cases}$ Or ce signe n'a pas de limite quand $x\to 0$ , donc $f$ n'est pas dérivable en $x_0=0$ . Cela fait sens du point de vue géométrique, puisqu'en ce point son graphe ne possède pas de droite tangente naturellement définie:

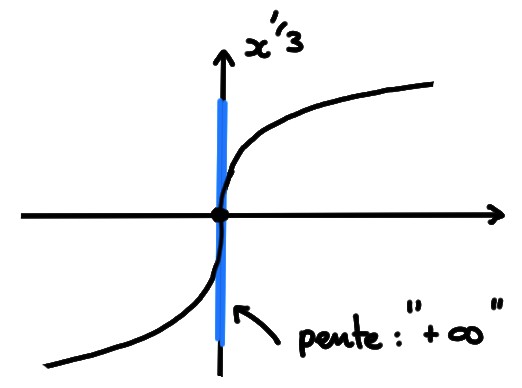
Exemple: Considérons $f(x)=\sqrt[3]{x}$ . Au point $x_0=0$ , la dérivée s'obtient en prenant la limite $x\to 0$ du rapport $\frac{f(x)-f(0)}{x-0}=\frac{\sqrt[3]{x}}{x}= \frac{1}{\sqrt[3]{x^2}}\,.$ Or cette limite est $+\infty$ , donc $f$ n'est pas dérivable en $x_0=0$ . Cela fait sens du point de vue géométrique, puisqu'en ce point son graphe possède une droite tangente, mais verticale (de pente infinie):

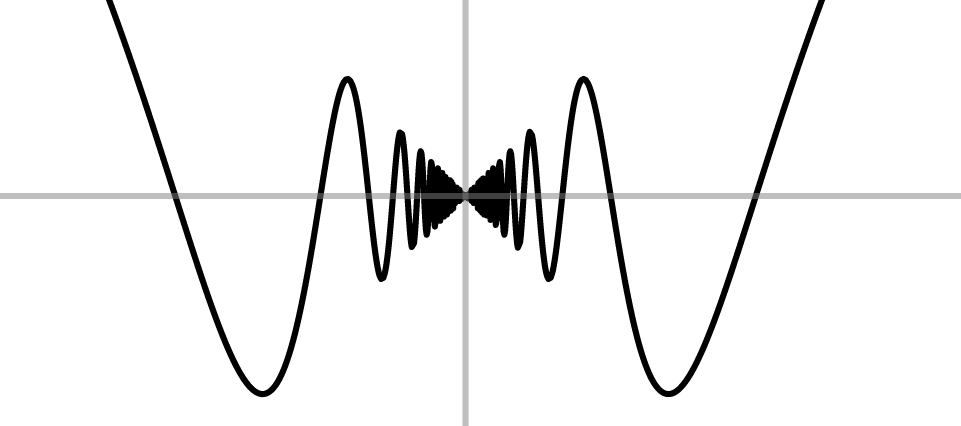
Exemple: Considérons $f(x)= \begin{cases} x\sin(\frac1x)&\text{ si }x\neq 0\,,\\ 0&\text{ si }x= 0\,. \end{cases}$ Au point $x_0=0$ , le rapport donnant la pente de la droite de la sécante est $\frac{f(x)-f(0)}{x-0}=\sin(\tfrac1x)\,,$ qui comme on le sait ne possède pas de limite lorsque $x\to 0$ . Donc $f$ n'est pas dérivable en $0$ :

Taux d'accroissement et la notation de Leibniz

De par sa signification géométrique, la dérivée est toujours une limite d'un quotient de deux quantités qui tendent vers zéro. (C'est pour ça que les indéterminations '' $\frac00$ '' sont si importantes!) $f'(x_0)=\lim_{x\to x_0}\frac{f(x)-f(x_0)}{x-x_0}\,.$ Interprétons cette limite en introduisant des nouvelles notations:

$\Delta f:= f(x)-f(x_0)$ représente l'incrément de la fonction.
$\Delta x:= x-x_0$ représente l'incrément de la variable.

D'un point de vue quantitatif, ces deux incréments sont petits lorsque $x$ est proche de $x_0$ ; $\Delta f$ dit exactement de combien $f$ varie lorsque $x$ s'écarte de $x_0$ d'une distance $\Delta x$ :

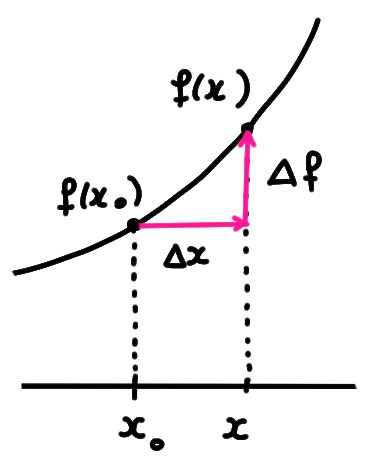
Ensuite, l'existence de la dérivée, $f'(x_0)=\lim_{x\to x_0}\frac{\Delta f}{\Delta x}\,,$ signifie que quand l'incrément $\Delta x$ est petit, alors $\Delta f$ est essentiellement proportionnel à $\Delta x$ , la constante de proportionnalité étant $f'(x_0)$ : $\Delta f\simeq f'(x_0)\Delta x$ On conclut que la dérivée $f'(x_0)$ représente le taux d'accroissement local de $f$ en $x_0$ : si on varie la variable de $x_0$ à $x_0+\Delta x$ , alors la valeur de la fonction passe de $f(x_0)$ à $f(x_0)+\Delta f$ , où $\Delta f$ est essentiellement proportionnel à $\Delta x$ , comme dans la relation ci-dessus.

Si on admet pendant un instant qu'il est possible de considérer des incréments infiniment petits, de la fonction et de la variable, que l'on notera respectivement

df

dx

, alors la dérivabilité de

f

x_0

signifie que ces deux infiniment petits sont proportionnels, la constante de proportionalité étant précisément la dérivée en

x_0

df=f'(x_0)dx\,.

La notation suivante, appelée notation de Leibniz, est donc naturelle:

f'(x_0) =\frac{df}{dx}(x_0)

Dérivabilité implique continuité

On l'a dit, pour que $f$ soit dérivable en $x_0$ , il faut que sa droite tangente soit bien définie; elle doit être assez lisse en $x_0$ . En particulier, son graphe ne peut pas faire de saut en $x_0$ :

Lemme: Si $f$ est dérivable en $x_0$ alors elle est continue en $x_0$ .

Preuve:

Si $f$ est dérivable en $x_0$ , alors en multipliant et divisant par $x-x_0$ , $\begin{aligned} \lim_{x\to x_0}(f(x)-f(x_0)) &= \lim_{x\to x_0}\Bigl[ \underbrace{\frac{f(x)-f(x_0)}{x-x_0}}_{\to f'(x_0)}\Bigr] \underbrace{(x-x_0)}_{\to 0}\\ &=f'(x_0)\cdot 0\\ &=0\,. \end{aligned}$ Donc $\lim_{x\to x_0}f(x)=f(x_0)$ , et donc $f$ est continue en $x_0$ .

Remarque: Attention, la réciproque de l'affirmation du lemme n'est pas vraie. C'est-à-dire que ''continuité'' n'implique pas ''dérivabilité''. Par exemple, on a vu que $f(x)=|x|$ n'est pas dérivable en $x_0=0$ , pourtant elle est bien continue en ce point.

On a vu ci-dessus plusieurs façons de construire une fonction qui est continue mais pas dérivable en un point. Il est naturel de se poser la question de savoir s'il existe des fonctions qui sont continues partout mais dérivables nulle part.

Considérons

f(x):= \sum_{n\geqslant 0} \frac{\cos(9^nx)}{2^n}\,.

Puisque

0\leqslant \left|\frac{\cos(9^nx)}{2^n}\right| \leqslant \frac{1}{2^n}\,,

cette fonction est bien définie pour tout

x\in \mathbb{R}

; elle est paire. Avec un peu plus de travail, on peut montrer qu'elle est aussi continue sur

\mathbb{R}

. Et avec encore un peu plus de travail, on peut montrer qu'elle n'est dérivable en aucun point de

\mathbb{R}

0,0

x

f(x)

Quiz 9.1-1 : Soit

f

dérivable en

x_0

, dont la dérivée est notée

f'(x_0)

. Alors

le nombre $f(x_0)$ est bien défini
$\displaystyle \lim_{h\to 0}\frac{f(x_0)-f(x_0-h)}{h}=f'(x_0)$
$\displaystyle \lim_{h\to 0}\frac{f(2x_0+h)-f(2x_0)}{h}=2f'(x_0)$
$\displaystyle \lim_{z\to x_0}\frac{f(z)-f(x_0)}{z-x_0}=f'(x_0)$
$\displaystyle \lim_{h\to 0}\frac{f(x_0+h^2)-f(x_0)}{h}=0$
$\displaystyle \lim_{h\to 0}\frac{f(x_0+h)^2-f(x_0)^2}{h}=f'(x_0)^2$

Quiz 9.1-2 : Soient

f,g:\mathbb{R}\to\mathbb{R}

dérivables en

x_0

. et soit

h:\mathbb{R}\to\mathbb{R}

définie par

h(x):= \begin{cases} f(x)&\text{ si }x\lt x_0\,,\\ g(x)&\text{ si }x\geqslant x_0\,.\\ \end{cases}

Alors

h

est dérivable en

x_0

, et

h'(x_0)=g'(x_0)

VRAI
FAUX

Quiz 9.1-3 : Soit

f

définie sur un intervalle ouvert contenant

x_0

, dérivable en

x_0

. Vrai ou faux?

$f$ est continue en $x_0$ .
Si $f(x_0)=2$ , alors $f'(x_0)=0$ .
⚡ $f$ est dérivable dans tout un voisinage de $x_0$ .
$f$ est continue dans un voisinage de $x_0$ .
Il existe $\delta>0$ tel que sur $]x_0-\delta,x_0+\delta[$ , le graphe de $f$ est une droite.
Il existe $\delta>0$ tel que $f$ est monotone sur $]x_0-\delta,x_0]$ et sur $[x_0,x_0+\delta[$ .