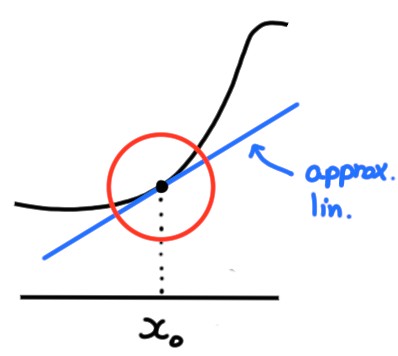
9.2 Dérivée et approximation linéaire
Répétons l'intérêt géométrique de la dérivabilité:
lorsque \(f\) est dérivable au point \(x_0\), le nombre
\(D=f'(x_0)\) représente la pente de la droite tangente au graphe de \(f\) au
point \((x_0,f(x_0))\).
Mais la dérivabilité représente aussi un intérêt
analytique, puisqu'elle
fournit une façon particulière de représenter la fonction au voisinage de
\(x_0\).
Commençons par illustrer ce fait sur un exemple simple:
Exemple:
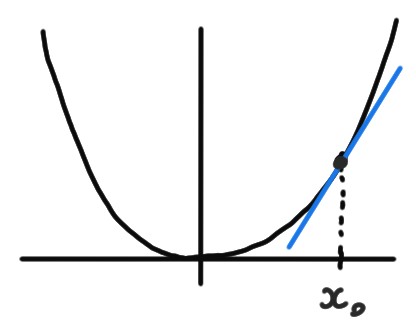
Considérons \(f(x)=x^2\) au voisinage de \(x_0=1\).
On a déjà vu dans la section précédente que \(f\) était dérivable en \(x_0=1\),
puisque
\[ f'(1)=\lim_{x\to 1}\frac{x^2-1^2}{x-1}=2\,.
\]
Si on définit, pour tout \(x\neq 1\),
\[ r_1(x):=
\frac{x^2-1^2}{x-1}-2\,,
\]
alors
\[
\lim_{x\to 1}r_1(x)=0\,.
\]
On peut de plus écrire
\[\begin{aligned}
x^2 &=1^2+(x^2-1^2)\\
&=1^2+\frac{x^2-1^2}{x-1}(x-1)\\
&=1^2+\Bigl(2+\bigl(\frac{x^2-1^2}{x-1}-2\bigr)\Bigr)(x-1)\\
&=1^2+\bigl(2+r_1(x)\bigr)(x-1)\\
&=\underbrace{1^2}_{=f(1)}+\underbrace{2}_{f'(1)}(x-1)+r_1(x)(x-1)\\
\end{aligned}\]
En d'autres termes, on peut écrire
\[\begin{aligned}
f(x)
&=f(1)+(f'(1)+r_1(x))(x-1)\\
&={\color{blue}f(1)+f'(1)(x-1)}+r_1(x)(x-1)
\end{aligned}\]
La fonction \({\color{blue}x\mapsto f(1)+f'(1)(x-1)}\) n'est autre que
l'équation de la droite tangente au graphe de \(x^2\) en \(x_0=1\);
elle approxime les valeurs de \(f(x)\) lorsque \(x\) est
proche de \(x_0\):
\[
f(x)\simeq {\color{blue}f(1)+f'(1)(x-1)}
\]
Puis, le terme ''\(+r_1(x)(x-1)\)'' est la correction qui donne l'écart entre la
vraie fonction et son approximation.
Ce que nous venons d'apprendre dans le cas \(f(x)=x^2\)
est vrai plus généralement:
Théorème: Soit \(f\) une fonction définie en \(x_0\) et dans son voisinage.
Alors:
\(f\) est dérivable en \(x_0\) et sa dérivée en ce point vaut \(f'(x_0)=D\)
si et seulement si
il existe une fonction \(r_{x_0}(x)\) définie dans un voisinage épointé de
\(x_0\)
telle que \(\lim_{x\to x_0}r_{x_0}(x)=0\), et telle que \(f\) peut être
représentée, dans ce voisinage, comme suit:
\[
f(x)=f(x_0)+(D+r_{x_0}(x))(x-x_0)\,.
\]
Preuve:
Si \(f\) est dérivable en \(x_0\) et \(f'(x_0)=D\), alors
\[\lim_{x\to x_0}
\frac{f(x)-f(x_0)}{x-x_0}=D\,,
\]
que l'on peut écrire
\[\lim_{x\to x_0}\Bigl\{\frac{f(x)-f(x_0)}{x-x_0}-D\Bigr\}=0\,.
\]
Donc si on définit la fonction
\[r_{x_0}(x):= \frac{f(x)-f(x_0)}{x-x_0}-D\,,
\]
alors par ce qui est écrit au-dessus, cette dernière satisfait
\(\lim_{x\to x_0}r_{x_0}(x)=0\). De plus, en isolant \(f(x)\) dans la définition
de \(r_{x_0}\), on voit que
\[ f(x)=f(x_0)+(D+r_{x_0}(x))(x-x_0)\,.
\]
Inversément, si cette relation est satisfaite pour une fonction \(r_{x_0}\)
satisfaisant \(\lim_{x\to x_0}r_{x_0}(x)=0\),
alors
\[ \frac{f(x)-f(x_0)}{x-x_0}=D+r_{x_0}(x)\,,
\]
et la limite de ce quotient existe puisque
\[
\lim_{x\to x_0} \frac{f(x)-f(x_0)}{x-x_0}
=D+\lim_{x\to x_0}r_{x_0}(x)=D\,,
\]
ce qui implique que \(f\) est dérivable en \(x_0\)
et que \(f'(x_0)=D\).
Une fonction dérivable en \(x_0\) peut donc s'écrire
\[\begin{aligned}
f(x)
&=f(x_0)+(f'(x_0)+r_{x_0}(x))(x-x_0)\\
&={\color{blue}f(x_0)+f'(x_0)(x-x_0)}+r_{x_0}(x)(x-x_0)\,,
\end{aligned}\]
où \(\lim_{x\to x_0}r_{x_0}(x)=0\).
Cette représentation est utile si on considère \(x\) proche de \(x_0\), car dans
ce cas le terme \(r_{x_0}(x)(x-x_0)\) est petit, et si on
le néglige, on obtient une approximation de \(f\) au voisinage de
\(x_0\), appelée l'approximation linéaire:
\[
f(x)\simeq {\color{blue}f(x_0)+f'(x_0)(x-x_0)}
\]
Cette approximation est celle qui consiste simplement à approximer le graphe de
\(f\), proche de \(x_0\), par celui
de sa droite tangente au point \((x_0,f(x_0))\):
Sur les deux premiers niveaux de régularité d'une fonction
On a pour l'instant deux notions de régularité pour une fonction \(f\) au
voisinage d'un point \(x_0\). Décrivons ce qu'elle représente en qualité
d'approximation.
-
La continuité:
Si \(f\) est continue en \(x_0\),
alors les valeurs de \(f(x)\) sont proches de \(f(x_0)\) lorsque \(x\)
est proche de \(x_0\), qui est
une approximation d'ordre zéro de \(f\) au voisinage de \(x_0\):
\[
\boxed{f(x)\simeq f(x_0)}
\]
-
La dérivabilité:
Si \(f\) est dérivable en \(x_0\), alors elle peut être représentée comme
ci-dessus, et si on néglige \(r_{x_0}(x)\),
on obtient
l'approximation linéaire, appelée aussi
approximation du premier ordre,
de \(f\) au voisinage de \(x_0\):
\[\boxed{f(x)\simeq {\color{blue}f(x_0)+f'(x_0)(x-x_0)}}\]
L'approximation à l'ordre zéro revient à approximer \(f(x)\)
par la constante \(f(x_0)\), mais
l'approximation linéaire est plus précise, puisqu'elle tient compte de
comment \(f\) varie au voisinage de \(x_0\)!
Comparons ces approximations sur un exemple simple:
Exemple:
Supposons que l'on veuille calculer \(1.998^4\).
Écrivons \(1.998^4=f(1.998)\), où \(f(x)=x^4\). Ce que l'on aimerait faire est
donc d'estimer la valeur de \(f\) en un point \(x=1.998\) qui est proche de
\(x_0=2\).
- À l'ordre zéro,
\[1.998^4=f(1.998)\simeq f(2)= 2^4=16\,.\]
- Au premier ordre,
\[\begin{aligned} 1.998^4=
f(1.998)&\simeq f(2)+f'(2)(1.998-2)\\
&= 2^4+4\cdot 2^3(1.998-2)\\
&=15.936
\end{aligned}\]
Sachant que la vraie valeur est \(1.998^4=15.9360959...\),
l'approximation à l'ordre zéro représente donc une erreur d'environ \(0.4\%\),
alors que celle du premier ordre, moins de \(0.001\%\)!
Nous verrons plus tard comment aller au-delà de l'approximation linéaire,
lorsque nous calculerons des développements limités.