9.11 La règle de Bernoulli-l'Hôpital

Nous allons voir maintenant un outil puissant qui, lorsqu'il est bien utilisé, permet d'étudier des indéterminations qu'aucune des méthodes présentées jusqu'ici ne permettait d'aborder.

Malgré tout, cet outil a un prix: il ne s'applique que dans certaines situations très particulières (voir les hypothèses ci-dessous), et sa justification est délicate.

Théorème:(Règle de Bernoulli-l'Hôpital) Soient \(f,g:]a,b[\to \mathbb{R}\) dérivables , telles que

  1. \(g(x)\neq 0\) et \(g'(x)\neq 0\) pour tout \(x\in ]a,b[\),
  2. la limite \[\lim_{x\to a^+}\frac{f(x)}{g(x)}\] est une indétermination du type ''\(\frac{0}{0}\)'' ou ''\(\frac{\pm\infty}{\pm\infty}\)'', c'est-à-dire que \[\lim_{x\to a^+}f(x)=\lim_{x\to a^+}g(x)=L\,,\] où \(L\in \{0,+\infty,-\infty\}\).
Si \[ \lim_{x\to a^+}\frac{f'(x)}{g'(x)}=R\,,\] où \(R\) est soit un réel, soit \(+\infty\), soit \(-\infty\), alors \[ \lim_{x\to a^+}\frac{f(x)}{g(x)}=R\,.\] Le résultat ci-dessus reste valable si on remplace partout

Commençons par traiter le cas où \(L=0\) et \(R\in \mathbb{R}\).

Fixons un \(x\in ]a,b[\) (que l'on fera ensuite \(\to a^+\)).



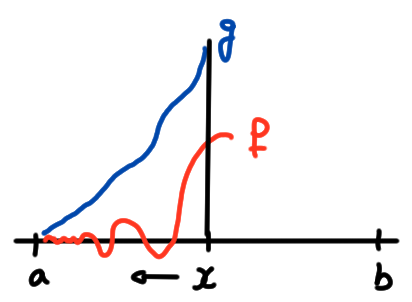
Comme \(\lim_{x\to a^+}f(x)=\lim_{x\to a^+}g(x)=L=0\), on peut prolonger \(f\) et \(g\) par continuité à \([a,x]\), en posant \(f(a):= 0\), \(g(a):= 0\). Comme maintenant \(f\) et \(g\) sont continues sur \([a,x]\) et dérivables sur \(]a,x[\), on peut utiliser la généralisation du Théorème des accroissements finis (fin de la section précédente), pour garantir l'existence d'un point \(c_x\in ]a,x[\) tel que \[ f'(c_x) =\frac{f(x)-f(a)}{g(x)-g(a)}g'(c_x)\,. \] Ceci nous permet de récrire le quotient (puisque ni \(g\) ni \(g'\) ne s'annulent dans \(]a,b[\)): \[ \frac{f(x)}{g(x)} =\frac{f(x)-0}{g(x)-0} =\frac{f(x)-f(a)}{g(x)-g(a)} =\frac{f'(c_x)}{g'(c_x)} \] Maintenant, prenons la limite \(x\to a^+\). Comme \(a\lt c_x\lt x\), on a \(c_x\to a^+\) lorsque \(x\to a^+\), et donc \[ \lim_{x\to a^+} \frac{f(x)}{g(x)}= \lim_{x\to a^+} \frac{f'(c_x)}{g'(c_x)}= \lim_{x\to a^+} \frac{f'(x)}{g'(x)}=R\,. \] Passons maintenant au cas où \(L=+\infty\) et \(R\in \mathbb{R}\).

On a donc \(\lim_{x\to a^+}f(x)=+\infty\), \(\lim_{x\to a^+}g(x)=+\infty\), et la limite \[ \lim_{x\to a^+}\frac{f'(x)}{g'(x)}=R \] est finie.
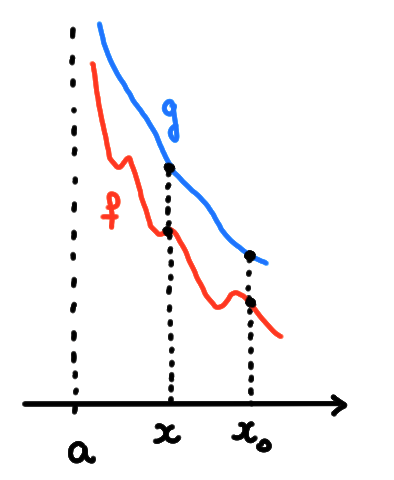
En préparation, fixons \(a\lt x\lt x_0\lt b\) et écrivons \[\begin{aligned} \Bigl|\frac{f(x)}{g(x)}-R\Bigr| &\leqslant \Bigl|\frac{f(x)}{g(x)}- \frac{f(x)-f(x_0)}{g(x)-g(x_0)} \Bigr|+ \Bigl| \frac{f(x)-f(x_0)}{g(x)-g(x_0)} -R\Bigr|\\ &\leqslant \Bigl|\frac{f(x)}{g(x)}\Bigr| \cdot \underbrace{\Bigl| 1-\frac{1-\frac{f(x_0)}{f(x)}}{1-\frac{g(x_0)}{g(x)}} \Bigr|}_{=:\varphi_{x_0}(x)}+ \underbrace{ \Bigl| \frac{f(x)-f(x_0)}{g(x)-g(x_0)} -R\Bigr|}_{=:\psi_{x_0}(x)}\\ \end{aligned}\] Maintenant, \[\begin{aligned} \Bigl|\frac{f(x)}{g(x)}-R\Bigr| &\leqslant \Bigl|\frac{f(x)}{g(x)}\Bigr| \varphi_{x_0}(x) +\psi_{x_0}(x)\\ &\leqslant \Bigl|\frac{f(x)}{g(x)}-R\Bigr| \varphi_{x_0}(x) +|R|\varphi_{x_0}(x) +\psi_{x_0}(x)\,, \end{aligned}\] et on peut isoler \(\Bigl|\frac{f(x)}{g(x)}-R\Bigr|\) dans cette dernière inégalité: \[\begin{aligned} \Bigl|\frac{f(x)}{g(x)}-R\Bigr| \leqslant \frac{|R|\varphi_{x_0}(x)+\psi_{x_0}(x)}{1-\varphi_{x_0}(x)}\,. \end{aligned}\] Voyons maintenant comment le côté droit peut être rendu arbitrairement petit en prenant \(x\) et \(x_0\) suffisamment proches de \(a\). D'abord, appliquons le TAFG sur \([x,x_0]\): il existe \(c_{x,x_0}\in ]x,x_0[\) tel que \[ \psi_{x_0}(x)=\Bigl| \frac{f(x)-f(x_0)}{g(x)-g(x_0)} -R\Bigr|=\Bigl| \frac{f'(c_{x,x_0})}{g'(c_{x,x_0})} -R\Bigr|\,. \] Par hypothèse, \(\frac{f'(x)}{g'(x)}\to R\). Donc en fixant \(\varepsilon\gt 0\), on peut prendre un \(x_0>a\) suffisamment proche de \(a\), de façon à ce que pour tout \(a\lt x\lt x_0\), \(0\leqslant \psi_{x_0}(x)\leqslant \varepsilon\). Ensuite, remarquons qu'à \(x_0\) fixé, on a toujours \(\lim_{x\to a^+}\varphi_{x_0}(x)=0\). On a donc \[ \lim_{x\to a^+} \Bigl|\frac{f(x)}{g(x)}-R\Bigr| \leqslant \varepsilon\,. \] Comme \(\varepsilon\gt 0\) est arbitraire, on a bien montré que \[ \lim_{x\to a^+}\frac{f(x)}{g(x)}=R\,, \] ce qu'on voulait démontrer.

La règle de BH, si elle s'applique de part et d'autre d'un point \(a\), permet évidemment de calculer des limites \(x\to a\):

Exemple: Étudions la limite \[ \lim_{x\to 0}\frac{\sin (x)-x}{x^3} \] Clairement, \(f(x)=\sin(x)-x\) et \(g(x)=x^3\) satisfont aux hypothèses du théorème: toutes deux sont dérivables dans un voisinage de \(x=0\), ni \(g\) ni \(g'\) ne s'annulent dans un voisinage épointé de \(x=0\), et toutes deux tendent vers zéro lorsque \(x\to 0\). On peut alors étudier la limite du quotient des dérivées : \[ \lim_{x\to 0}\frac{f'(x)}{g'(x)}= \lim_{x\to 0}\frac{\cos (x)-1}{3x^2}=-\frac16 \] Comme cette limite existe et est finie, on peut conclure par le théorème que \[ \lim_{x\to 0}\frac{\sin (x)-x}{x^3}= \lim_{x\to 0}\frac{f(x)}{g(x)}= \lim_{x\to 0}\frac{f'(x)}{g'(x)}=-\frac16\,. \]

\(\bigstar\) On n'utilise surtout pas la règle de BH pour calculer des limites fondamentales, telles que \[ \lim_{x\to 0}\frac{\sin(x)}{x}=1 \quad{\color{red}!!!} \] En effet si on voulait utiliser BH pour cette limite, on devrait dériver le sinus: \((\sin (x))'=\cos(x)\). Or si on relit la preuve de comment on montre que la dérivée du sinus c'est le cosinus, on se rend compte qu'elle repose sur la connaissance de ... \(\lim_{x\to 0}\frac{\sin(x)}{x}\)!

Donc la limite ''\(\lim_{x\to 0}\frac{\sin(x)}{x}=1\)'' doit être considérée comme fondamentale, calculée uniquement à partir de la définition de base du sinus, dans le cercle trigonométrique.

Même si elle est formulée pour des indéterminations qui concernent des quotients, la règle de BH permet en fait de calculer des indéterminations de tous les types. Ceci se fait en récrivant la fonction dont ont aimerait calculer la limite, de façon a y faire apparaître un quotient.

Exemple: (Une indétermination ''\(0\cdot \infty\)'') \[\begin{aligned} \lim_{x\to 0^+}x\log(x) = \lim_{x\to 0^+}\frac{\log(x)}{\frac1x} &\stackrel{BH}{=} \lim_{x\to 0^+}\frac{\frac1x}{-\frac1{x^2}}\\ &=-\lim_{x\to 0^+}x=0\,. \end{aligned}\]

Exemple: (Une indétermination ''\(1^\infty\)'') \[\lim_{x\to +\infty}\Bigl(\frac{x}{x+2}\Bigr)^x\,.\] Puisque \(\frac{x}{x+2}>0\) pour tout \(x\) suffisamment grand et positif, on peut exponentier: \[ \Bigl(\frac{x}{x+2}\Bigr)^x =\exp\Bigl( x\log\bigl(\frac{x}{x+2}\bigr) \Bigr) \] Comme l'exponentielle est continue, on pourra rentrer la limite (une fois qu'on aura vérifié que la limite dans l'exposant existe): \[ \lim_{x\to +\infty} \bigl(\frac{x}{x+2}\bigr)^x =\exp\Bigl(\lim_{x\to +\infty} x\log\bigl(\frac{x}{x+2}\bigr) \Bigr) \] Étudions donc la limite à l'intérieur de l'exponentielle. En réarrangeant, on fait apparaître une limite ''\(\frac00\)'': \[\begin{aligned} \lim_{x\to +\infty} x\log\bigl(\frac{x}{x+2}\bigr) &=\lim_{x\to +\infty} \frac{\log(x)-\log(x+2)}{\frac1x} \\ &\stackrel{BH}{=}\lim_{x\to +\infty}\frac{\frac1x-\frac1{x+2}}{-\frac1{x^2}} \\ &=-2\lim_{x\to +\infty} \frac{x^2}{x(x+2)}=-2\,. \end{aligned}\] On a donc \[\lim_{x\to +\infty}\Bigl(\frac{x}{x+2}\Bigr)^x=\exp(-2)\,.\]

\(\bigstar\) Avant de se lancer corps et âme dans l'utilisation de la règle de BH, on a tout intérêt de s'arrêter un moment et se demander si elle est vraiment nécessaire, et surtout si ses hypothèses sont satisfaites...

Exemple: Considérons \[ \lim_{x\to 0}\frac{\sin(x^7)\cos(\sin(x^8))}{x^7}\,.\] Numérateur et dénominateur sont des fonctions dérivables , mais est-ce qu'on veut vraiment se mettre à dériver le numérateur?

Or on voit que la composée \(\cos(\sin(x^8))\) a une limite qui vaut \(1\) (différente de zéro), donc elle ne pose pas de problème, on peut simplement la séparer du reste, puis faire un changement de variable \(z=x^7\), pour obtenir \[\begin{aligned} \lim_{x\to 0}\frac{\sin(x^7)\cos(\sin(x^8))}{x^7} &= \underbrace{\bigl(\lim_{x\to 0}\cos(\sin(x^8))\bigr)}_{=1} \Bigl( \lim_{x\to 0}\frac{\sin(x^7)}{x^7} \Bigr)\\ &=\lim_{z\to 0}\frac{\sin(z)}{z}=1\,. \end{aligned}\]

Exemple: Considérons \[ \lim_{x\to \infty}\frac{x+\sin(x^2)}{3x} \] Cette limite est de la forme \(\lim_{x\to+\infty}\frac{f(x)}{g(x)}\) et se calcule directement, en mettant en évidence le terme dominant au numérateur, \[ \lim_{x\to \infty}\frac{x+\sin(x^2)}{3x} = \lim_{x\to \infty}\frac{x(1+\frac{\sin(x^2)}{x})}{3x} = \lim_{x\to \infty}\left(\frac{1}{3}+\frac{\sin(x^2)}{3x}\right)=\frac13\,. \] Cette limite fournit un exemple de cas où numérateur et dénominateur sont tous les deux dérivables, mais le quotient \(\frac{f'(x)}{g'(x)}\) n'a pas de limite puisque \[ \frac{f'(x)}{g'(x)}= \frac{1+2x\cos(x^2)}{1}=1+2x\cos(x^2)\,, \] qui n'a pas de limite lorsque \(x\to \infty\). Donc la règle de BH ne s'applique pas.



Utilisation répétée de la règle

L'idée utilisée dans ce dernier exemple permet de revenir sur quelque chose que nous avons déjà rencontré dans le chapitre sur les suites, à savoir la hiérarchie de comportements à l'infini des polynômes, exponentielles et logarithmes.

On aura alors parfois besoin d'utiliser la règle de BH plus d'une fois:

Exemple: \[ \lim_{x\to \infty}\frac{x^2}{e^{3x}} \stackrel{BH}{=} \lim_{x\to \infty}\frac{2x}{3e^{3x}} \stackrel{BH}{=} \frac23 \lim_{x\to \infty}\frac{1}{3e^{3x}} =\frac{2}{9}\times 0=0\,. \]

Généralisons:

Lemme: Pour toute base \(a\gt 1\), tout \(\alpha \gt 0\) et tout \(m\gt 0\), \[ \lim_{x\to\infty} \frac{x^\alpha}{a^{mx}}=0\,,\qquad \lim_{x\to\infty} \frac{(\log_a(x))^\alpha}{x^m}=0\,. \]

Considérons la première limite. Deux remarques permettent de simplifier le calcul.

  • D'abord, on peut toujours écrire \[ a^{mx}=e^{m'x} \,, \] où \(m'=m\log(a)\). Or puisque \(a\gt 1\), on a \(m'\gt 0\). Donc il suffit de démontrer le résultat pour la base \(e\).
  • Puisque \(\alpha\leqslant \lfloor\alpha\rfloor+1\), il suffit aussi de démontrer le résultat pour des \(\alpha\) entiers, c.-à-d. \(\alpha=k\in \mathbb{N}\).
Fixons donc \(m\gt 0\), et montrons que pour tout entier \(k\geqslant 1\), \[ \lim_{x\to\infty} \frac{x^k}{e^{mx}}=0\,. \] Dans le cas où \(k=1\), \[ \lim_{x\to \infty}\frac{x}{e^{mx}} \stackrel{BH}{=} \lim_{x\to \infty}\frac{1}{me^{mx}} =0\,. \] Supposons alors que le résultat a été démontré pour un entier \(k\). On a \[\begin{aligned} \lim_{x\to \infty}\frac{x^{k+1}}{e^{mx}} &\stackrel{BH}{=} \lim_{x\to \infty}\frac{(x^{k+1})'}{(e^{mx})'}\\ &=\frac{k+1}{m} \lim_{x\to \infty}\frac{x^k}{e^{mx}}\\ &=0\,, \end{aligned}\] et donc le résultat est vrai pour \(k+1\).

La deuxième limite est une conséquence de la première. En effet, ne posant \(y=\log_a(x)\), \[ \lim_{x\to\infty} \frac{(\log_a(x))^\alpha}{x^m}= \lim_{y\to\infty}\frac{y^\alpha}{a^{my}}=0\,. \]

Quiz 9.11-1 : Soient \(f,g:]a,b[\to \mathbb{R}\) dérivables, et \(g\) telle que \(g(x)\neq 0\) et \(g'(x)\neq 0\) pour tout \(x\in ]a,b[\). Parmi les affirmations ci-dessous, lesquelles sont toujours vraies?
  1. () Si \(\lim_{x\to a^+}f(x)\) et \(\lim_{x\to a^+}g(x)\) existent, alors \(\lim_{x\to a^+}\frac{f(x)}{g(x)}\) existe.
  2. () Si \(f\) et \(g\) peuvent être prolongées par continuité à \([a,b[\), alors \(\lim_{x\to a^+}\frac{f(x)}{g(x)}\) existe.
  3. () Si \(\lim_{x\to a^+}f(x)\) et \(\lim_{x\to a^+}g(x)\) existent, alors \(\lim_{x\to a^+}\frac{f'(x)}{g'(x)}\) existe.
  4. () Si \(\lim_{x\to a^+}f(x)\) et \(\lim_{x\to a^+}g(x)\) existent, alors \(\lim_{x\to a^+}\frac{f(x)}{g(x)}\) existe.
  5. () \( \lim_{x\to a^+}\frac{f(x)}{g(x)} = \lim_{x\to a^+}\bigl(\frac{f(x)}{g(x)}\bigr)' \).
  6. () \(\lim_{x\to a^+}\bigl(\frac{f(x)}{g(x)}\bigr)' =\lim_{x\to a^+}\frac{f'(x)}{g'(x)}\).
  7. () \(\lim_{x\to a^+}\frac{f(x)}{g(x)}=\lim_{x\to a^+}\frac{f'(x)}{g'(x)}\).
  8. () Si \(\lim_{x\to a^+}f(x)=\lim_{x\to a^+}g(x)=0\), et si si \(\lim_{x\to a^+}\frac{f(x)}{g(x)}\) n'existe pas, alors \(\lim_{x\to a^+}\frac{f'(x)}{g'(x)}\) n'existe pas.
  9. () Si \(\lim_{x\to a^+}\frac{f'(x)}{g'(x)}=D\), alors \(f'\) et \(g'\) sont bornées sur \(]a,b[\).
  10. () Si \(\lim_{x\to a^+}\frac{f'(x)}{g'(x)}\) n'existe pas, alors \(\lim_{x\to a^+}\frac{f(x)}{g(x)}\) n'existe pas.
  11. () Si \(\lim_{x\to a^+}\frac{f(x)}{g(x)}=+\infty\), alors \(\lim_{x\to a^+}\frac{f'(x)}{g'(x)}=+\infty\).
  12. () Si \(\lim_{x\to a^+}\frac{f'(x)}{g'(x)}=D\), et si \(\alpha,\beta\) sont des constantes, alors \(\lim_{x\to a^+}\frac{f(x)+\alpha}{g(x)+\beta}=D\).
Quiz 9.11-2 : Vrai ou faux?
  1. () \(\displaystyle \lim_{x\to 0^+} \frac{1}{x}=\lim_{x\to 0^+}\frac{0}{1}\)
  2. () \(\displaystyle \lim_{x\to 0} \frac{x^2-1}{x^2+1} =\lim_{x\to 0}\frac{(x^2-1)'}{(x^2+1)'}\)
  3. () \(\displaystyle \lim_{x\to \infty} \frac{x^2-1}{x^2+1} =\lim_{x\to \infty}\frac{(x^2-1)'}{(x^2+1)'}\)




---- (Dernière modification: 2022-11-23 (11:14:12)) ----