Analyse 1 | S. Friedli (EPFL)

2.4 Exponentielle complexe

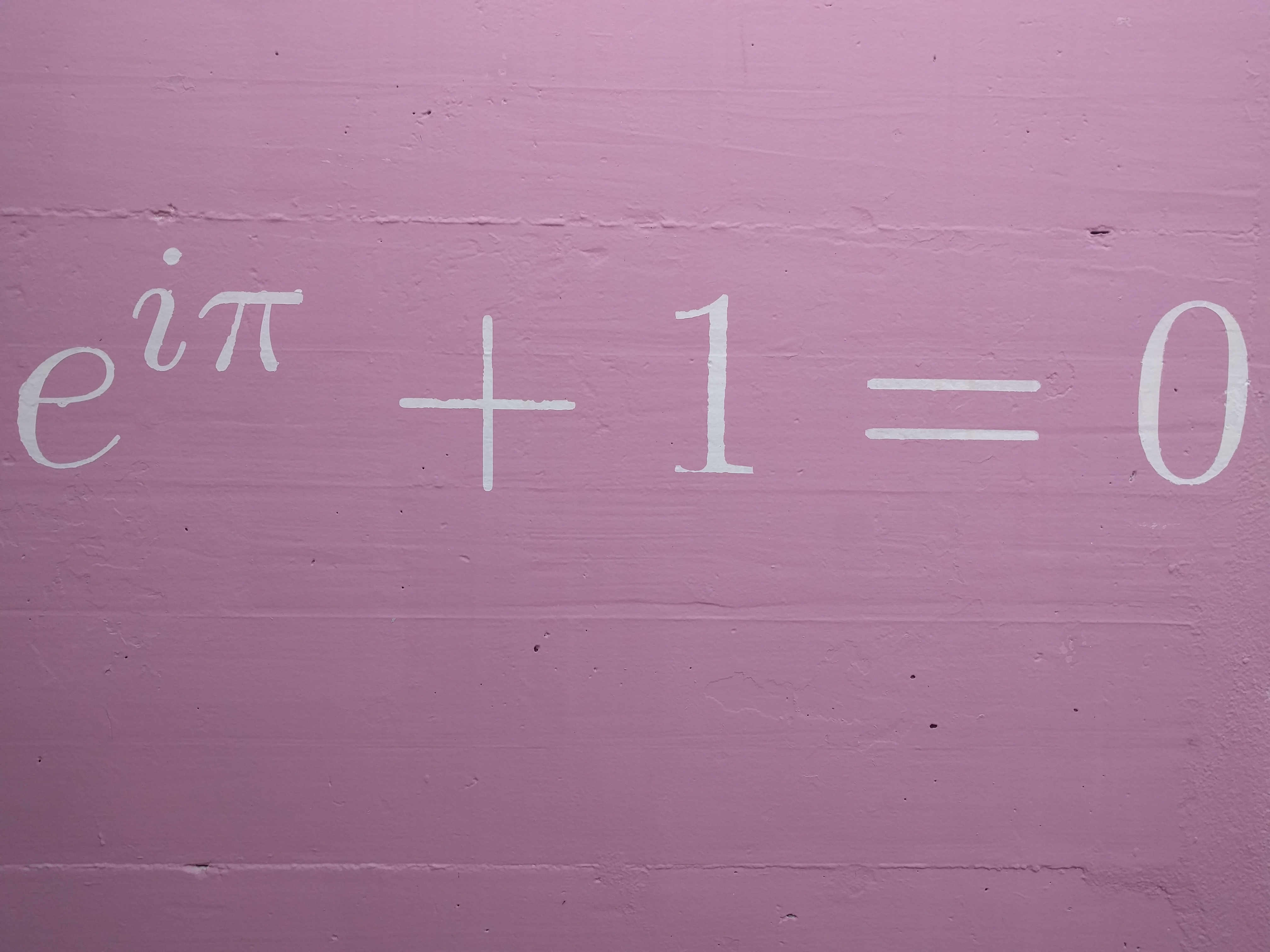
Considérons la fonction \(\varphi:\mathbb{R}\to \mathbb{C}\) définie par \[\varphi(\theta):= \cos \theta +\mathsf{i} \sin \theta\,. \] Par la propriété de l'argument, \[\varphi(\theta)\varphi(\theta')=\varphi(\theta+\theta')\,.\] Cette relation n'est pas sans rappeler la propriété de base de la fonction exponentielle (définie sur \(\mathbb{R}\)): \[e^xe^y=e^{x+y}\,.\]

On peut profiter de cette analogie pour introduire une nouvelle fonction sur \(\mathbb{C}\):

Soit \(z\in \mathbb{C}\). Alors l'exponentielle de \(z\) est définie par \[ \exp(z):= e^{\mathrm{Re}(z)}(\cos(\mathrm{Im}(z))+\mathsf{i}\sin(\mathrm{Im}(z))). \]

Remarque: Dans cette définition, la partie ''\(e^{\mathrm{Re}(z)}\)'' est l'exponentielle classique (du réel \(\mathrm{Re}(z)\)), et ''\(\cos\)'' et ''\(\sin\)'' sont les fonctions trigonométriques usuelles. En particulier, si \(\mathrm{Im}(z)=0\), c'est-à-dire si \(z\) est un nombre réel, alors \(\exp(z)\) coïncide avec ''l'exponentielle de \(z\)'' au sens classique du terme. Pour cette raison, par abus de notation, nous écrirons souvent ''\(e^z\)'' au lieu de ''\(\exp(z)\)''.

(Propriétés de \(z\mapsto \exp(z)\))

\(e^ze^{z'}=e^{z+z'}\)
\(|e^z|=e^{\mathrm{Re}(z)}\)
\(\mathrm{Arg } (e^z)=\mathrm{Im}(z)\)
\(e^{z+2k\pi \mathsf{i}}=e^z\) (périodicité dans la direction imaginaire)

Preuve:

1) suit de la formule pour l'argument: si \(z=x+\mathsf{i} y\), \(z'=x'+\mathsf{i} y'\), alors en utilisant la fonction \(\varphi\), \[\begin{aligned} e^{z+z'} &=e^{(x+x')+\mathsf{i} (y+y')}\\ &=e^{x+x'}\bigl(\cos(y+y')+\mathsf{i} \sin(y+y')\bigr)\\ &=e^{x+x'}\varphi(y+y')\\ &=e^xe^{x'}\varphi(y)\varphi(y')\\ &=e^ze^{z'}\,. \end{aligned}\] 2) Si \(z=x+\mathsf{i} y\), alors \(|e^z|=|e^x\varphi(y)|=|e^x||\varphi(y)|=|e^x|=e^x\).

3) et 4) suivent directement de la définition de \(e^z\).

La définition de \(e^z\) donnée ci-dessus peut paraître un peu arbitraire. En analyse complexe, l'exponentielle est en général définie par une série (nous ne traiterons pas des séries complexes dans ce cours): \[ \exp(z):= \sum_{n\geqslant 0}\frac{z^n}{n!}\,.\] On peut montrer que cette définition satisfait à toutes les propriétés énoncées ci-dessus, et qu'elle coïncide avec l'expression que nous avons utilisée pour définir \(e^z\).

Exponentielle de nombres purement imaginaires, Formule d'Euler

L'exponentielle d'un nombre purement imaginaire \(\mathsf{i} y\) n'est donc autre que \(\varphi(y)\): \[ e^{\mathsf{i} y}= \cos y+\mathsf{i} \sin y\,. \] Ainsi, la fonction \(y\mapsto e^{\mathsf{i} y}\) jouit des propriétés suivantes:

\(|e^{\mathsf{i} y}|=1\)
\(\overline{e^{\mathsf{i} y}}=e^{\mathsf{i} (-y)}\)
\(e^{\mathsf{i} y}e^{\mathsf{i} y'}=e^{\mathsf{i} (y+y')}\)
\(\frac{e^{\mathsf{i} y}}{e^{\mathsf{i} y'}}=e^{\mathsf{i} (y- y')}\)
\(\sin y=\frac{e^{\mathsf{i} y}-e^{-\mathsf{i} y}}{2\mathsf{i} }\)
\(\cos y=\frac{e^{\mathsf{i} y}+e^{-\mathsf{i} y}}{2}\)

Observons \(e^{\mathsf{i} y}\) pour quelques valeurs particulières de \(y\).

\(e^{\mathsf{i} \frac{\pi}{2}}=\mathsf{i}\),
\(e^{\mathsf{i} 2k\pi}=1\qquad \forall k\in \mathbb{Z}\),
Formule d'Euler: \(e^{\mathsf{i}\pi}=-1\).

(Création: "Oeuvre 24", de GF)

Représentation polaire/exponentielle

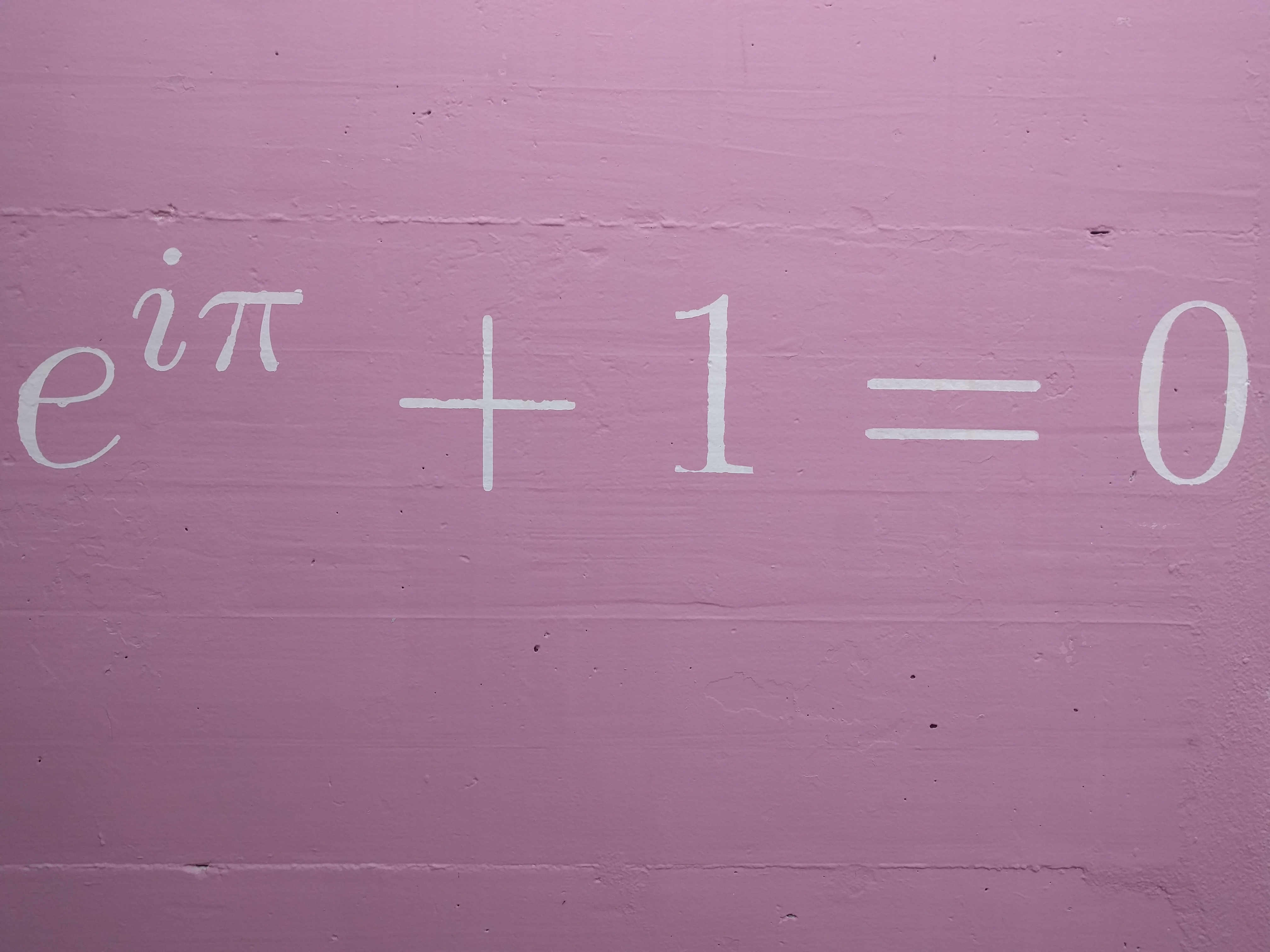
Si un complexe \(z\in \mathbb{C}\) est tel que \(|z|=r\) et \(\mathrm{Arg }(z)=\theta\), on peut maintenant le représenter sous forme polaire/exponentielle (on dira plus simplement polaire): \[ \boxed{z=re^{\mathsf{i} \theta}\,.} \] La formule de Moivre devient maintenant: \[ z^n=\bigl(re^{\mathsf{i} \theta}\bigr)^n =r^ne^{\mathsf{i} n\theta} =r^n\bigl(\cos(n\theta)+\mathsf{i} \sin(n\theta)\bigr)\,. \]

La représentation exponentielle des nombres complexes est utile dans de nombreuses situations, par exemple pour calculer des puissances:

Exemple: Si \(z=2-2\sqrt{3}\mathsf{i}\), que vaut \(z^{999}\)?

Calculer cette puissance en multipliant \(z\) par lui-même \(998\) fois, à l'aide de la définition du produit complexe uniquement, n'est probablement pas une bonne idée. Utilisons plutôt la forme polaire de \(z\), déjà calculée plus haut: \[z=4e^{\mathsf{i} (-\frac{\pi}{3})}\,.\] Par la formule de Moivre, \[\begin{aligned} z^{999} =4^{999}e^{\mathsf{i} (-999\frac{\pi}{3})} =4^{999}e^{\mathsf{i} (-333 \pi)} &=4^{999}e^{\mathsf{i} (-166\cdot 2 \pi-\pi)}\\ &=4^{999}\underbrace{e^{\mathsf{i} (-166\cdot 2 \pi)}}_{=1} \underbrace{e^{\mathsf{i} (-\pi)}}_{=-1}\\ &=-4^{999}\,. \end{aligned}\]

Exemple: \[ \Bigl( \frac{1-\mathsf{i}}{1+\mathsf{i}} \Bigr)^4 = \Bigl( \frac{\sqrt{2}e^{\mathsf{i} (-\frac{\pi}{4})}}{\sqrt{2}e^{\mathsf{i}\frac{\pi}{4}}} \Bigr)^4 =\bigl(e^{\mathsf{i} (-\frac{\pi}{2})}\bigr)^4 =e^{\mathsf{i} (-2\pi)}=1\,. \]

Finalement, la notation polaire/exponentielle est utile pour résoudre des équations en une variable complexe \(z\). Pour cela, on aura souvent besoin de se souvenir que si \(z,z'\) sont deux nombres complexes écrits sous forme polaire, \(z=re^{\mathsf{i} \theta}\) et \(z'=r'e^{\mathsf{i} \theta'}\), alors \[ z=z'\qquad \Leftrightarrow \qquad r=r'\text{ et }\theta=\theta'+2k\pi \] pour un entier \(k\) qui peut être quelconque.

Exemple: Considérons l'équation complexe \[ \Bigl(\frac{z}{\overline{z}}\Bigr)^2=z\,. \] On se rend vite compte, en essayant de poser \(z=a+\mathsf{i} b\), que l'approche cartésienne n'est pas la bonne. Écrivons plutôt \(z=re^{\mathsf{i} \theta}\). L'équation devient alors \[ \Bigl(\frac{re^{\mathsf{i} \theta}}{re^{-\mathsf{i} \theta}}\Bigr)^2=re^{\mathsf{i} \theta}\,, \] qui est \[ e^{\mathsf{i} 4\theta}=re^{\mathsf{i} \theta}\,. \] On a donc (voir la remarque ci-dessus) \(r=1\), et \[ 4\theta=\theta+2k\pi\,, \] ce qui donne \(\theta=k\frac{2\pi}{3}\), et donc toute solution est de la forme \(z=e^{\mathsf{i} k\frac{2\pi}{3}}\). On obtient trois solutions distinctes en prenant \(k=0,1,2\).

Dans la section suivante, nous verrons l'utilité de la notation polaire/exponentielle pour trouver les racines d'un nombre complexe.