Analyse 1 | S. Friedli (EPFL)

10.1 Introduction

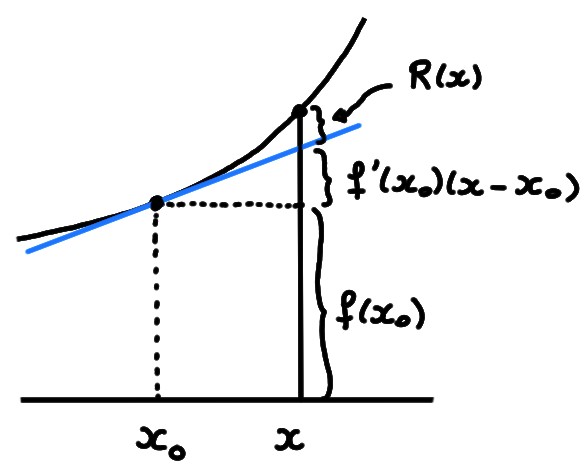
Rappelons que la dérivabilité d'une fonction \(f\) en un point \(x_0\) permet de la représenter au voisinage de ce point:

\[\begin{aligned} f(x) &=f(x_0)+(f'(x_0)+r_{x_0}(x))(x-x_0)\\ &= \underbrace{\underbrace{f(x_0)}_{ \text{ordre zéro}}+f'(x_0)(x-x_0)}_{1^{er}\,\,ordre} +\underbrace{r_{x_0}(x)(x-x_0)}_{=R(x)\text{, reste}}\,, \end{aligned}\] où \(\lim_{x\to x_0}r_{x_0}(x)=0\).

Cette dernière expression doit être lue de la façon suivante: pour un \(x\) proche de \(x_0\), \(f(x)\) se calcule en prenant

sa valeur en \(x_0\), \(f(x_0)\), à laquelle il faut rajouter...
une correction linéaire en \(x-x_0\), \(f'(x_0)(x-x_0)\), à laquelle on rajoute encore...
un reste \(R(x)=(x-x_0)r_{x_0}(x)\).

La somme des trois termes donne exactement \(f(x)\), et ils sont en ordre décroissant d'importance (voir la figure ci-dessus): la correction linéaire est petite puisque \(x-x_0\) est petit, et le reste est petit puisque \(\lim_{x\to x_0}R(x)=0\). Mais en fait le reste est beaucoup plus petit que la correction linéaire, puisque \[ \lim_{x\to x_0}\frac{R(x)}{x-x_0}= \lim_{x\to x_0}r_{x_0}(x)= 0\,. \]

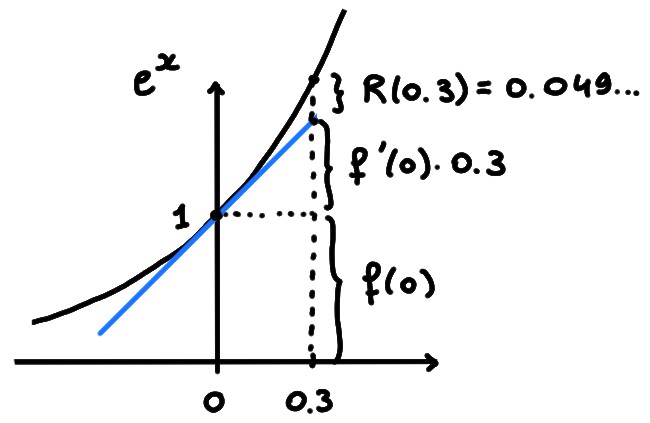
En d'autres termes, \(R(x)\) est ''doublement'' petit, puisque c'est le produit de \(x-x_0\) (qui est petit lorsque \(x\) est proche de \(x_0\)) par \(r_{x_0}(x)\) (qui est aussi petit lorsque \(x\) est proche de \(x_0\)).

Exemple: Considérons \(f(x)=e^x\), au voisinage du point \(x_0=0\). Si on s'intéresse par exemple au point \(x=0.3\), on obtient \[ f(0.3)= \underbrace{f(0)}_{1} +\underbrace{f'(0)0.3}_{0.3} +\underbrace{0.3 r_0(0.3)}_{0.0498\dots} =1.3498\dots \]

Une question naturelle est de savoir si il est possible d'obtenir une approximation de la fonction qui aille au-delà de l'approximation linéaire (et de son reste): pour un point fixé \(x\neq x_0\), peut-on approximer \(f(x)\) à l'aide d'une expression qui soit plus précise que l'approximation linéaire?

La première amélioration naturelle serait une approximation quadratique (du deuxième ordre), qui du point de vue graphique consiste à approximer le graphe, localement, par une parabole plutôt que par une droite. Une telle approximation, si elle existe, est plus précise puisqu'elle doit tenir compte de la courbure du graphe dans le voisinage du point.

Après l'approximation quadratique, on pourra essayer de produire une approximation cubique, et ainsi de suite, on pourra considérer des approximations d'ordres de plus en plus grand, à l'aide de polynômes. C'est le but de ce chapitre que de présenter cette construction, et de donner des conditions sur \(f\) qui garantissent que ces approximations sont possibles.

Certaines formules/expressions, dans ce chapitre, sont assez longues. On pourra donc augmenter la largeur du texte visible avec les boutons ''\(+\)'' et ''\(-\)'' dans la barre ci-dessus.