Analyse réelle | S. Friedli

2.3 Combinaisons linéaires et parties engendrés

En algèbre linéaire, une façon standard et non-triviale d'obtenir de nouveaux vecteurs à partir d'une famille donnée est de former des combinaisons linéaires.

Soient \(\boldsymbol{v}_1,\boldsymbol{v}_2,\dots,\boldsymbol{v}_k\) des vecteurs de \(\mathbb{R}^n\). Une somme du type \[ \lambda_1\boldsymbol{v}_1+\dots+\lambda_k\boldsymbol{v}_k\,, \] où les \(\lambda_1,\lambda_2,\dots,\lambda_k\) sont des scalaires fixés, est appelée combinaison linéaire des vecteurs \(\boldsymbol{v}_1,\dots,\boldsymbol{v}_k\). Les scalaires \(\lambda_j\) sont les coefficients de la combinaison linéaire.

Exemple: Dans \(\mathbb{R}^2\), considérons \(\boldsymbol{v}_1= \begin{pmatrix} 3\\5 \end{pmatrix}\), \(\boldsymbol{v}_2= \begin{pmatrix} -1\\2 \end{pmatrix}\). En prenant \(\lambda_1=-2\), \(\lambda_2=3\), \[ \lambda_1\boldsymbol{v}_1+\lambda_2\boldsymbol{v}_2= -2\binom{3}{5}+3\binom{-1}{2}= \binom{-9}{-4}\,. \] Choisissons maintenant un troisième vecteur: \(\boldsymbol{w}= \begin{pmatrix} 5\\-2 \end{pmatrix} \), et posons la question: est-il possible d'écrire \(\boldsymbol{w}\) comme une combinaison linéaire de \(\boldsymbol{v}_1\) et \(\boldsymbol{v}_2\)? Il s'agit donc de voir si il existe des scalaires \(\lambda_1,\lambda_2\) tels que \[ \lambda_1\boldsymbol{v}_1+\lambda_2\boldsymbol{v}_2=\boldsymbol{w}\,. \] Lorsqu'on exprime cette relation en composantes, \[ \binom{3\lambda_1-\lambda_2}{5\lambda_1+2\lambda_2} = \binom{5}{-2} \] Puisque deux vecteurs sont égaux si et seulement si leurs composantes sont égales deux-à-deux, on en déduit que \(\lambda_1\) et \(\lambda_2\) doivent être solution du système \[ \left\{ \begin{array}{ccccc} 3\lambda_1 &-& \lambda_2 &=&5 \\ 5\lambda_1 &+& 2\lambda_2 &=&-2 \end{array} \right. \] La solution de ce système est unique, donnée par \(\lambda_1=\frac{8}{11}\), \(\lambda_2=\frac{-31}{11}\). On en déduit que \(\boldsymbol{w}\) est bien combinaison linéaire de \(\boldsymbol{v}_1\) et \(\boldsymbol{v}_2\): \[ \boldsymbol{w}=\tfrac{8}{11}\boldsymbol{v}_1-\tfrac{31}{11}\boldsymbol{v}_2\,. \]

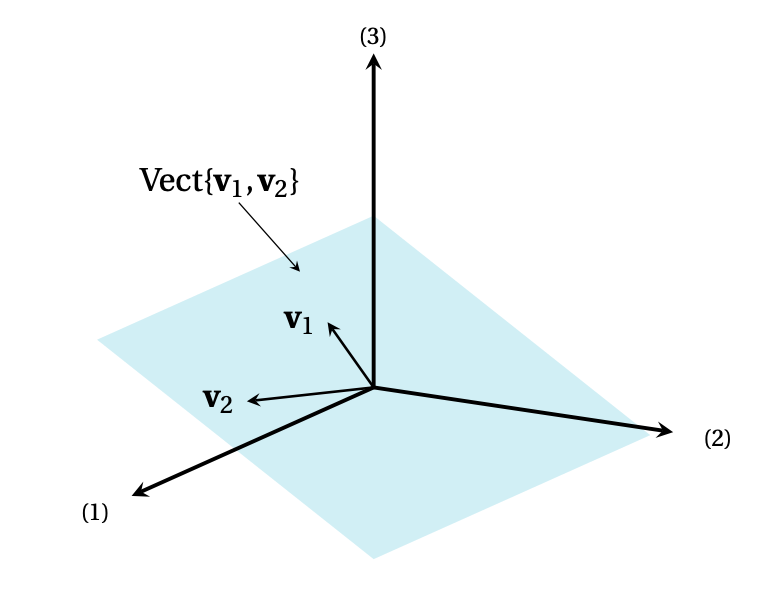
Plus généralement, fixons deux vecteurs \(\boldsymbol{v}_1\) et \(\boldsymbol{v}_2\) dans le plan, et considérons toutes les combinaisons linéaires de la forme \[ \boldsymbol{w}=\lambda_1\boldsymbol{v}_1+\lambda_2\boldsymbol{v}_2\,,\qquad \lambda_1,\lambda_2\in \mathbb{R}\,. \]

On remarque que

Si \(\boldsymbol{v}_1\) et \(\boldsymbol{v}_2\) ne sont pas colinéaires, alors toutes les combinaisons linéaires possibles de \(\boldsymbol{v}_1\) et \(\boldsymbol{v}_2\) remplissent le plan, dans le sens suivant: n'importe quel vecteur \(\boldsymbol{w}\) peut s'écrire comme combinaison linéaire de \(\boldsymbol{v}_1\) et \(\boldsymbol{v}_2\).
Si \(\boldsymbol{v}_1\) et \(\boldsymbol{v}_2\) sont colinéaires, alors seulement certains vecteurs \(\boldsymbol{w}\) du plan peuvent s'écrire comme combinaison linéaire de \(\boldsymbol{v}_1\) et \(\boldsymbol{v}_2\) (essentiellement ceux qui sont sur la droite portée par \(\boldsymbol{v}_1\) et \(\boldsymbol{v}_2\)).

Exemple: Dans \(\mathbb{R}^3\), considérons \[ \boldsymbol{v}_1= \begin{pmatrix} -3\\ 2\\ 0 \end{pmatrix} \,,\quad \boldsymbol{v}_2= \begin{pmatrix} 1\\ 1\\ -1 \end{pmatrix} \,,\quad \boldsymbol{w}= \begin{pmatrix} 4\\ 0\\ 3 \end{pmatrix} \] Est-ce que \(\boldsymbol{w}\) est combinaison linéaire de \(\boldsymbol{v}_1\) et \(\boldsymbol{v}_2\)? Pour le savoir, cherchons \(\lambda_1,\lambda_2\) tels que \[ \lambda_1\boldsymbol{v}_1+\lambda_2\boldsymbol{v}_2=\boldsymbol{w}\,, \] qui mène au système \[ \left\{ \begin{array}{ccccc} -3\lambda_1 &+& \lambda_2 &=&4 \\ 2\lambda_1 &+& \lambda_2 &=&0 \\ &-& \lambda_2 &=&3 \end{array} \right. \] Ce système est incompatible, donc \(\boldsymbol{w}\) ne peut pas s'écrire comme combinaison linéaire de \(\boldsymbol{v}_1\) et \(\boldsymbol{v}_2\).

Dans ce dernier exemple, on a résolu un problème de combinaison linéaire en l'exprimant sous la forme d'un système linéaire. Dans la section suivante nous ferons l'inverse, en montrant qu'un système linéaire peut se traduire en un problème de combinaison linéaire.

Parties engendrées

Soient \(\boldsymbol{v}_1,\dots,\boldsymbol{v}_p\) des vecteurs de \(\mathbb{R}^n\) donnés. La partie de \(\mathbb{R}^n\) engendrée par la famille \(\{\boldsymbol{v}_1,\dots,\boldsymbol{v}_p\}\), notée \[\mathrm{Vect}\{\boldsymbol{v}_1,\dots,\boldsymbol{v}_p\}\,,\] est définie comme l'ensemble des vecteurs de \(\mathbb{R}^n\) qui peuvent s'écrire comme combinaison linéaire des vecteurs \(\boldsymbol{v}_1,\dots,\boldsymbol{v}_p\): \[\boldsymbol{w}=\lambda_1\boldsymbol{v}_1+\cdots+\lambda_p\boldsymbol{v}_p\,.\]

La partie engendrée par une famille de vecteurs, c'est l'ensemble de toutes les combinaisons linéaires possibles de ces vecteurs.

Remarque: En anglais, \(\mathrm{Vect}\{\boldsymbol{v}_1,\dots,\boldsymbol{v}_p\}\) se note \(\mathrm{Span}\,\{\boldsymbol{v}_1,\dots,\boldsymbol{v}_p\}\).

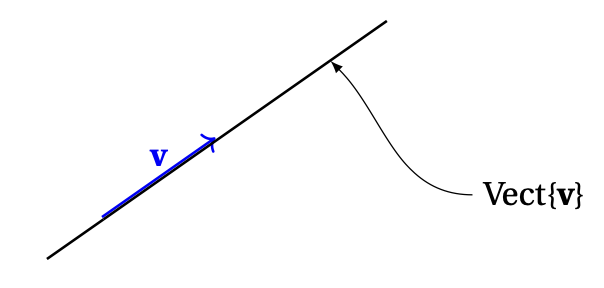
Pour les familles contenant un ou deux vecteurs:

Lorsqu'on considère une famille \(\{\boldsymbol{v}\}\) contenant un seul vecteur non-nul \(\boldsymbol{v}\), \(\mathrm{Vect}\{\boldsymbol{v}\}\) est constitué de tous les vecteurs colinéaires à \(\boldsymbol{v}\), c'est-à-dire de la forme \(\boldsymbol{w}=\lambda\boldsymbol{v}\). Il est donc naturel d'interpréter \(\mathrm{Vect}\{\boldsymbol{v}\}\) comme la droite de \(\mathbb{R}^n\) engendrée par \(\boldsymbol{v}\), passant par l'origine:
Lorsqu'on considère une famille \(\{\boldsymbol{v}_1,\boldsymbol{v}_2\}\) contenant deux vecteurs non-colinéaires, on interprète \(\mathrm{Vect}\{\boldsymbol{v}_1,\boldsymbol{v}_2\}\) comme le plan de \(\mathbb{R}^n\) engendrée par \(\boldsymbol{v}_1\) et \(\boldsymbol{v}_2\), passant par l'origine:

Même si cette terminologie (''droite'', ''plan'') est empruntée à la géométrie du plan \((n=2)\) et de l'espace (\(n=3\)), nous l'utiliserons aussi dans les dimensions supérieures (\(n\gt 3\)).

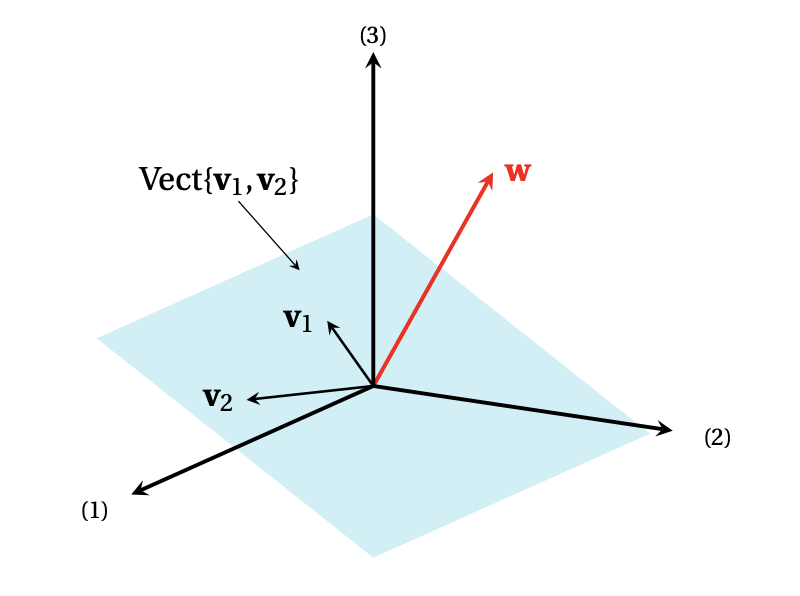
Exemple: Plus haut, nous avions défini \[ \boldsymbol{v}_1= \begin{pmatrix} -3\\ 2\\ 0 \end{pmatrix} \,,\quad \boldsymbol{v}_2= \begin{pmatrix} 1\\ 1\\ -1 \end{pmatrix} \,,\quad \boldsymbol{w}= \begin{pmatrix} 4\\ 0\\ 3 \end{pmatrix}\,, \] et montré que \(\boldsymbol{w}\) n'est pas combinaison linéaire de \(\boldsymbol{v}_1\) et \(\boldsymbol{v}_2\). Nous pouvons maintenant interpréter ceci en disant que \(\boldsymbol{w}\) n'est pas dans le plan engendré par \(\boldsymbol{v}_1\) et \(\boldsymbol{v}_2\):

La base canonique de \(\mathbb{R}^n\)

Définissons, pour tout \(k=1,\dots,n\), le vecteur \(\boldsymbol{e}_k\in\mathbb{R}^n\) comme étant le vecteur dont toutes les composantes sont nulles, sauf la \(k\)-ème, qui vaut \(1\). \[ \boldsymbol{e}_1= \begin{pmatrix} 1\\ 0\\ 0\\ \vdots\\ 0\\ 0 \end{pmatrix}\,,\quad \boldsymbol{e}_2= \begin{pmatrix} 0\\ 1\\ 0\\ \vdots\\ 0\\ 0 \end{pmatrix}\,,\quad \cdots\qquad \boldsymbol{e}_n= \begin{pmatrix} 0\\ 0\\ 0\\ \vdots\\ 0\\ 1 \end{pmatrix}\,. \] Cette famille de vecteur peut être utilisée pour décomposer n'importe quel vecteur, comme suit: \[\begin{aligned} \boldsymbol{x}= \begin{pmatrix} x_1\\ x_2\\ \vdots\\ x_n \end{pmatrix} &= \begin{pmatrix} x_1\\ 0\\ \vdots\\ 0 \end{pmatrix} + \begin{pmatrix} 0\\ x_2\\ \vdots\\ 0 \end{pmatrix} +\cdots + \begin{pmatrix} 0\\ 0\\ \vdots\\ x_n \end{pmatrix}\\ &= x_1\begin{pmatrix} 1\\ 0\\ \vdots\\ 0 \end{pmatrix} + x_2\begin{pmatrix} 0\\ 1\\ \vdots\\ 0 \end{pmatrix} +\cdots + x_n\begin{pmatrix} 0\\ 0\\ \vdots\\ 1 \end{pmatrix}\\ &= x_1\boldsymbol{e}_1+x_2\boldsymbol{e}_2+\cdots+x_n\boldsymbol{e}_n\,. \end{aligned}\] En d'autres termes, \[ \mathbb{R}^n=\mathrm{Vect}\{\boldsymbol{e}_1,\dots,\boldsymbol{e}_n\}\,. \] Plus tard, on appellera \(\{\boldsymbol{e}_1,\dots,\boldsymbol{e}_n\}\) la base canonique de \(\mathbb{R}^n\).

Quiz 2.3-1 : Soient \(\boldsymbol{v}_1,\dots,\boldsymbol{v}_p\) des vecteurs de \(\mathbb{R}^3\), et soit \[W:= \mathrm{Vect}\{\boldsymbol{v}_1,\dots,\boldsymbol{v}_p\}\,.\] Vrai ou faux?

\(W\) contient le vecteur nul \(\boldsymbol{0}\).
Si \(p=2\), alors \(W\) est un plan.
Si \(p>2\), alors \(W\) n'est pas un plan.
Si \(\boldsymbol{w}_1,\boldsymbol{w}_2\in W\), alors \(\alpha_1\boldsymbol{w}_1+\alpha_2\boldsymbol{w}_2\in W\), peu importe les valeurs des scalaires \(\alpha_1,\alpha_2\).