2.1 Définitions
Dans ce chapitre, nous laissons les systèmes de côté un instant, pour
introduire le langage de base nécessaire au
développement de l'algèbre linéaire dans les espaces \(\mathbb{R}^n\), \(n\geqslant 1\).
Pour commencer, nous introduirons la notion de vecteur, centrale en algèbre
linéaire, et particulièrement utile pour décrire les systèmes.
Objectifs de ce chapitre:
- (O.1) exprimer un vecteur de \(\mathbb{R}^n\) comme combinaison linéaire d'autres vecteurs, si possible;
- (O.2) déterminer si un vecteur est dans la partie engendrée par une famille de vecteurs en résolvant le SEL associé;
- (O.3) déterminer si une famille de vecteurs est libre ou liée en résolvant le SEL associé.
Nouveau vocabulaire dans ce chapitre:
- combinaison linéaire
- vecteurs colinéaires
- famille liée (ou linéairement dépendante)
- famille libre (ou linéairement indépendante)
- partie engendrée
Vecteurs
On l'a déjà mentionné plus haut: toute
liste de nombres réels \((x_1,x_2,\dots, x_n)\) peut être identifiée avec un
point de l'espace \(\mathbb{R}^n\). Or les points de \(\mathbb{R}^n\) sont plus facilement
manipulables lorsqu'on les interprète comme des objets appelés vecteurs.
On identifiera donc \((x_1,\dots,x_n)\) avec le vecteur
(dit aussi vecteur-colonne), noté
\[
\boldsymbol{x}=
\begin{pmatrix}
x_1\\
x_2\\
\vdots\\
x_n
\end{pmatrix}\,.
\]
En analyse, \(\mathbb{R}^n\) est considéré comme un ensemble de points. En
algèbre linéaire, \(\mathbb{R}^n\) est considéré comme un ensemble de vecteurs.
Il est clair que la liste \((x_1,\dots,x_n)\) et le vecteur \(\boldsymbol{x}\)
contiennent la même information, mais ici
il faut interpréter \(\boldsymbol{x}\) comme
le déplacement depuis l'origine jusqu'au
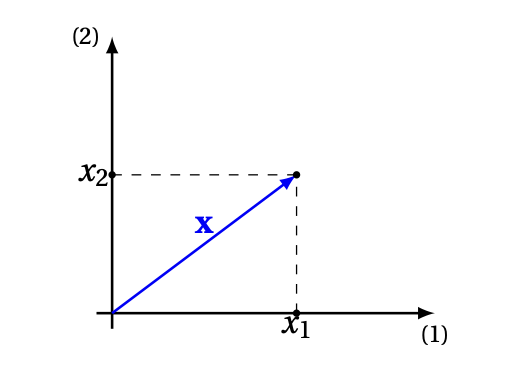
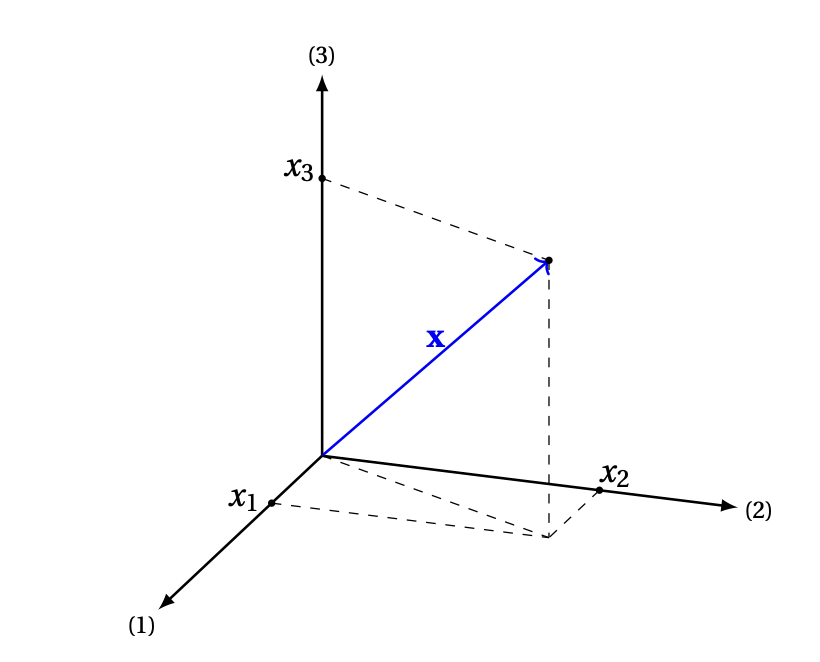
point \((x_1,x_2,\dots, x_n)\). Par exemple, dans
le plan \(\mathbb{R}^2\),
ou dans l'espace \(\mathbb{R}^3\):
Remarque:
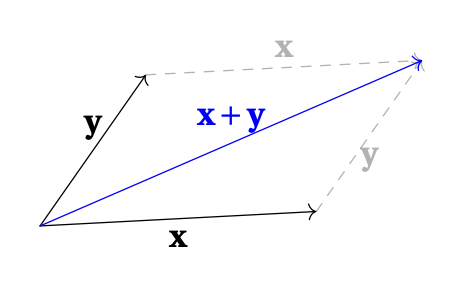
En petites dimensions, \(n=2\) et \(n=3\), l'addition vectorielle peut
s'interpréter géométriquement comme la règle du parallélogramme:
On comprend ici que c'est l'interprétation d'un vecteur
comme à un
déplacement qui rend cette opération
d'addition naturelle.
Le vecteur nul est celui dont toutes les composantes sont égales à zéro.
On le notera
\[ \boldsymbol{0}=
\begin{pmatrix}
0\\
0\\
\vdots\\
0
\end{pmatrix}\,.
\]
Par définition, on a \(0\boldsymbol{x}=\boldsymbol{0}\).
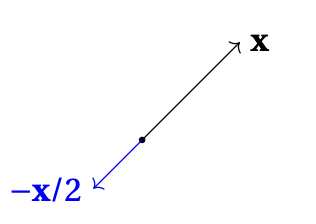
Pour tout vecteur \(\boldsymbol{x}\),
on appelle opposé de \(\boldsymbol{x}\) le vecteur \(-\boldsymbol{x}:=
(-1)\boldsymbol{x}\).
Les opérations d'addition et de multiplication par un scalaire permettent
de manipuler les vecteurs à l'aide de calculs.
Ces calculs obéissent aux règles standard de l'arithmétique:
Pour tous vecteurs \(\boldsymbol{x}\), \(\boldsymbol{y}\), \(\boldsymbol{z}\) de \(\mathbb{R}^n\), et pour
tous scalaires \(\lambda,\mu\in \mathbb{R}\),
- (V.1)
\(\boldsymbol{x}+\boldsymbol{y}=\boldsymbol{y}+\boldsymbol{x}\) (commutativité);
- (V.2)
\(\boldsymbol{x}+(\boldsymbol{y}+\boldsymbol{z})= (\boldsymbol{x}+\boldsymbol{y})+\boldsymbol{z}\) (associativité);
- (V.3)
\(\boldsymbol{x}+\boldsymbol{0}=\boldsymbol{0}+\boldsymbol{x}=\boldsymbol{x}\)\,;
- (V.4)
\(\boldsymbol{x}+(-\boldsymbol{x})=(-\boldsymbol{x})+\boldsymbol{x}=\boldsymbol{0}\)\,;
- (V.5)
\(\lambda(\boldsymbol{x}+\boldsymbol{y})=\lambda\boldsymbol{x}+\lambda\boldsymbol{y}\) (distributivité I);
- (V.6)
\((\lambda+\mu)\boldsymbol{x}=\lambda\boldsymbol{x}+\mu\boldsymbol{x}\) (distributivité II);
- (V.7)
\((\lambda\mu)\boldsymbol{x}=\lambda(\mu\boldsymbol{x})=\mu(\lambda \boldsymbol{x})\) (distributivité mixte);
- (V.8)
\(1 \boldsymbol{x} = \boldsymbol{x}\).
Preuve:
Ces propriétés ne font que refléter une propriété élémentaire semblable, valide
dans le corps des nombres réels.
Ci-dessous, on indiquera par le symbole \(\overset{{\color{red}!}}{=}\)
une identité obtenue en utilisant une propriété de base dans les réels, pour
chacune des composantes:
\item[
\hyperlink{(V.1)}
{(V.1)}]
\[
\boldsymbol{x}+\boldsymbol{y}
=
\begin{pmatrix}
x_1+y_1\\
x_2+y_2\\
\vdots\\
x_n+y_n
\end{pmatrix}
\overset{{\color{red}!}}{=}
\begin{pmatrix}
y_1+x_1\\
y_2+x_2\\
\vdots\\
y_n+x_n
\end{pmatrix}
=
\boldsymbol{y}+\boldsymbol{x}\,;
\]
\item[
\hyperlink{(V.2)}
{(V.2)}]
\[\begin{aligned}
\boldsymbol{x}+(\boldsymbol{y}+\boldsymbol{z})&=
\begin{pmatrix}
x_1\\
x_2\\
\vdots\\
x_n
\end{pmatrix}
+
\begin{pmatrix}
y_1+z_1\\
y_2+z_2\\
\vdots\\
y_n+z_n
\end{pmatrix}
=
\begin{pmatrix}
x_1+(y_1+z_1)\\
x_2+(y_2+z_2)\\
\vdots\\
x_n+(y_n+z_n)
\end{pmatrix}
\overset{{\color{red}!}}{=}
\begin{pmatrix}
(x_1+y_1)+z_1\\
(x_2+y_2)+z_2\\
\vdots\\
(x_n+y_n)+z_n
\end{pmatrix}
=
\begin{pmatrix}
x_1+y_1\\
x_2+y_2\\
\vdots\\
x_n+y_n
\end{pmatrix}
+
\begin{pmatrix}
z_1\\
z_2\\
\vdots\\
z_n
\end{pmatrix}
=
(\boldsymbol{x}+\boldsymbol{y})+\boldsymbol{z}\,;
\end{aligned}\]
\item[
\hyperlink{(V.3)}
{(V.3)}]
\[\begin{aligned}
\boldsymbol{x}+\boldsymbol{0}&=
\begin{pmatrix}
x_1+0\\
x_2+0\\
\vdots\\
x_n+0
\end{pmatrix}
\overset{{\color{red}!}}{=}
\begin{pmatrix}
x_1\\
x_2\\
\vdots\\
x_n
\end{pmatrix}
\overset{{\color{red}!}}{=}
\begin{pmatrix}
0+x_1\\
0+x_2\\
\vdots\\
0+x_n
\end{pmatrix}
=
\boldsymbol{0}+\boldsymbol{x}\,;
\end{aligned}\]
\item[
\hyperlink{(V.4)}
{(V.4)}]
\[\begin{aligned}
\boldsymbol{x}+(-\boldsymbol{x})&=
\begin{pmatrix}
x_1+(-x_1)\\
x_2+(-x_2)\\
\vdots\\
x_n+(-x_n)
\end{pmatrix}
\overset{{\color{red}!}}{=}
\begin{pmatrix}
0\\
0\\
\vdots\\
0
\end{pmatrix}
\overset{{\color{red}!}}{=}
\begin{pmatrix}
(-x_1)+x_1\\
(-x_2)+x_2\\
\vdots\\
(-x_n)+x_n
\end{pmatrix}
=
(-\boldsymbol{x})+\boldsymbol{x}\,;
\end{aligned}\]
\item[
\hyperlink{(V.5)}
{(V.5)}]
\[\begin{aligned}
\lambda(\boldsymbol{x}+\boldsymbol{y})&=
\lambda
\begin{pmatrix}
x_1+y_1\\
x_2+y_2\\
\vdots\\
x_n+y_n
\end{pmatrix}
=
\begin{pmatrix}
\lambda(x_1+y_1)\\
\lambda(x_2+y_2)\\
\vdots\\
\lambda(x_n+y_n)
\end{pmatrix}
\overset{{\color{red}!}}{=}
\begin{pmatrix}
\lambda x_1+\lambda y_1\\
\lambda x_2+\lambda y_2\\
\vdots\\
\lambda x_n+\lambda y_n
\end{pmatrix}
=\lambda \boldsymbol{x}+\lambda \boldsymbol{y}\,;
\end{aligned}\]
\item[
\hyperlink{(V.6)}
{(V.6)}]
\[\begin{aligned}
(\lambda+\mu)\boldsymbol{x}&=
\begin{pmatrix}
(\lambda+\mu)x_1\\
(\lambda+\mu)x_2\\
\vdots\\
(\lambda+\mu)x_n
\end{pmatrix}
\overset{{\color{red}!}}{=}
\begin{pmatrix}
\lambda x_1+\mu x_1\\
\lambda x_2+\mu x_2\\
\vdots\\
\lambda x_n+\mu x_n
\end{pmatrix}=\lambda \boldsymbol{x}+\mu\boldsymbol{x}\,;
\end{aligned}\]
\item[
\hyperlink{(V.7)}
{(V.7)}]
\[\begin{aligned}
(\lambda\mu)\boldsymbol{x}
&=
\begin{pmatrix}
(\lambda\mu)x_1\\
(\lambda\mu)x_2\\
\vdots\\
(\lambda\mu)x_n
\end{pmatrix}
\overset{{\color{red}!}}{=}
\begin{pmatrix}
\lambda(\mu x_1)\\
\lambda(\mu x_2)\\
\vdots\\
\lambda(\mu x_n)
\end{pmatrix}=\lambda(\mu\boldsymbol{x})
\overset{{\color{red}!}}{=}
\begin{pmatrix}
\mu(\lambda x_1)\\
\mu(\lambda x_2)\\
\vdots\\
\mu(\lambda x_n)
\end{pmatrix}=\mu(\lambda\boldsymbol{x})\,;
\end{aligned}\]
\item[
\hyperlink{(V.8)}
{(V.8)}]
\[\begin{aligned}
1 \boldsymbol{x}
&=
\begin{pmatrix}
1.x_1\\
1.x_2\\
\vdots\\
1.x_n
\end{pmatrix}
\overset{{\color{red}!}}{=}
\begin{pmatrix}
x_1\\
x_2\\
\vdots\\
x_n
\end{pmatrix}=\boldsymbol{x}.
\end{aligned}\]
Avec ces propriétés, on peut résoudre des équations vectorielles, dont
l'inconnue est un vecteur \(\boldsymbol{x}\), de la même façon qu'on
résout des équations élémentaires où l'inconnue est un réel \(x\).
Exemple:
Considérons deux vecteurs \(\boldsymbol{a},\boldsymbol{b}\in \mathbb{R}^n\) fixés,
et étudions l'équation vectorielle
\[
2\boldsymbol{a}-3\boldsymbol{x}=5\boldsymbol{x}+7\boldsymbol{b}\,.
\]
Utilisons les propriétés démontrées ci-dessus pour isoler \(\boldsymbol{x}\),
comme on le fait quand on résout une équation en arithmétique élémentaire.
Rajoutons \(+3\boldsymbol{x}\) des deux côtés.
Du côté gauche, détaillons l'utilisation des propriétés:
\[
2\boldsymbol{a}-3\boldsymbol{x}+3\boldsymbol{x}=2\boldsymbol{a}+(-3+3)\boldsymbol{x}=2\boldsymbol{a}+0\boldsymbol{x}=2\boldsymbol{a}
+\boldsymbol{0}=2\boldsymbol{a}\,.
\]
En procédant de même du côté droit,
on obtient
\[
2\boldsymbol{a}=8\boldsymbol{x}+7\boldsymbol{b}\,.
\]
En soustrayant \(7\boldsymbol{b}\) des deux côtés,
\[
8\boldsymbol{x}=2\boldsymbol{a}-7\boldsymbol{b}\,,
\]
puis en multipliant par \(\frac18\),
\[
\boldsymbol{x}=\tfrac14\boldsymbol{a}-\tfrac78\boldsymbol{b}\,.
\]