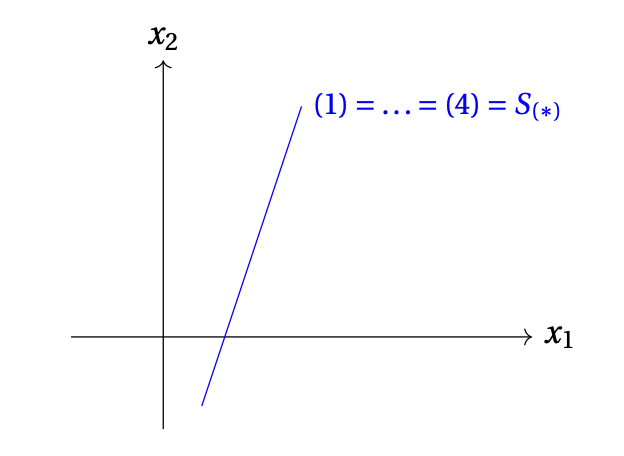
1.3 Sur le nombre de solutions d'un système linéaire

Un de nos objectifs dans ce qui suit sera de trouver des conditions suffisantes pour déterminer si un système est compatible ou incompatible.

Mais avant cela, nous allons énoncer une propriété générale, satisfaite par n'importe quel système linéaire, concernant le nombre de solutions qu'il peut posséder.

Théorème: Si un système est compatible, alors soit il possède exactement une solution, soit il en possède une infinité.

Considérons un système de taille \(m\times n\) de la forme \((*)\), que l'on suppose être compatible. Si sa solution n'est pas unique, c'est qu'il existe au moins deux familles distinctes, que l'on notera \((\bar{x}_1,\dots,\bar{x}_n)\) et \((\bar{y}_1,\dots,\bar{y}_n)\), qui sont toutes deux solutions de \((*)\); cela signifie qu'elles satisfont toutes les contraintes: pour tout \(k=1,2,\dots,m\), on a d'une part que \[ \begin{array}{ccccccc} a_{k,1}\bar{x}_1 &+& \cdots &+& a_{k,n}\bar{x_n} &=&b_k \end{array} \] et d'autre part que \[ \begin{array}{ccccccc} a_{k,1}\bar{y}_1 &+& \cdots &+& a_{k,n}\bar{y_n} &=&b_k\,. \end{array} \] Prenons alors un réel \(\lambda\) quelconque, différent de \(0\) et de \(1\), et définissons la famille \((\bar{z}_1,\dots,\bar{z}_n)\), où \[ z_j:= \lambda \bar{x}_j+(1-\lambda)\bar{y}_j\,,\quad j=1,2,\dots,n\,. \] Montrons alors que \((\bar{z}_1,\dots,\bar{z}_n)\) est aussi solution, en montrant qu'elle satisfait chacune des \(m\) contraintes du système. En effet, \[\begin{aligned} a_{k,1}\bar{z}_1&+\cdots+a_{k,n}\bar{z_n}\\ =&a_{k,1}(\lambda \bar{x}_1+(1-\lambda)\bar{y}_1) +\cdots +a_{k,n}(\lambda \bar{x}_n+(1-\lambda)\bar{y}_n)\\ =&\lambda \bigl(\underbrace{a_{k,1}\bar{x}_1+\cdots+a_{k,n}\bar{x_n}}_{=b_k}\bigr) +(1-\lambda)\bigl(\underbrace{a_{k,1}\bar{y}_1+\cdots+a_{k,n}\bar{y_n}}_{=b_k}\bigr)\\ =&\lambda b_k+(1-\lambda)b_k\\ =& b_k\,, \end{aligned}\] ce qui signifie que la \(k\)-ème contrainte est satisfaite. Puisque \((\bar{x}_1,\dots,\bar{x}_n)\) et \((\bar{y}_1,\dots,\bar{y}_n)\) sont distinctes, il existe au moins un \(k\) tel que \(\bar{x}_k\neq \bar{y}_k\). Cela signifie que si \(\lambda\) n'est égal ni à \(0\) ni à \(1\), le nombre \(z_k=\lambda\bar{x}_k+(1-\lambda)\bar{y}_k\) est différent à la fois de \(\bar{x}_k\) et de \(\bar{y}_k\). On peut donc, en choisissant \(\lambda\), construire autant de nouvelles solutions. Ceci signifie que le système possède une infinité de solutions.

Remarque: Un peu plus loin dans le cours, nous redonnerons la preuve de ce théorème, mais en utilisant le langage vectoriel, ce qui la rendra plus transparente.

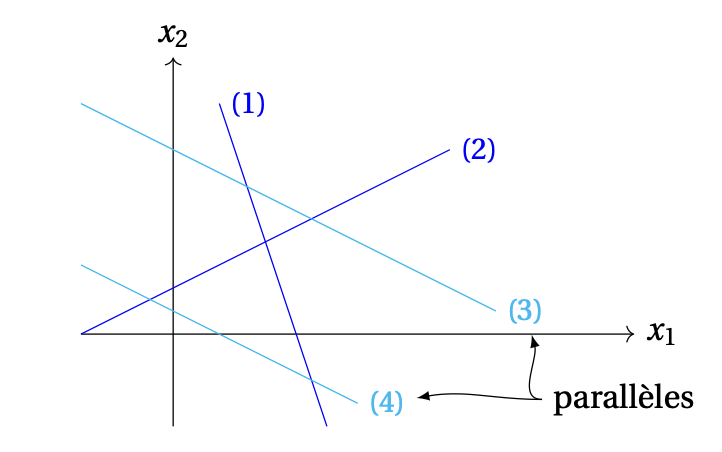
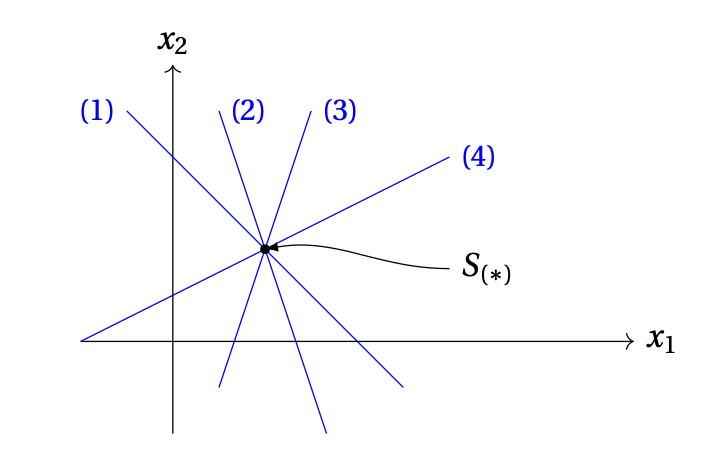
En d'autres termes, le nombre de solutions de n'importe quel système linéaire ne peut être que \(0\) (s'il est incompatible), \(1\) ou \(\infty\). Plus tard on se référera à ce résultat comme le Théorème ''\(0,1,\infty\)''.

Pour des petites valeurs de \(n\), l'affirmation du Théorème ''\(0,1,\infty\)'' peut s'interpréter géométriquement.

Interprétation géométrique dans le cas \(n=2\)

Fixons \(n=2\), et considérons un système de taille \(m\times 2\): \[ (*) \left\{ \begin{array}{ccccc} a_{1,1}x_1 &+& a_{1,2}x_2 &=&b_1\,, \\ a_{2,1}x_1 &+& a_{2,2}x_2 &=&b_2\,, \\ && &\vdots& \\ a_{m,1}x_1 &+& a_{m,2}x_2 &=&b_m\,. \end{array} \right. \] Ici, une paire \((x_1,x_2)\) peut s'interpréter comme les coordonnées d'un point dans le plan, relativement à un repère orthonormé fixé. Aussi, on sait (voir cours de géométrie analytique) qu'une contrainte de la forme \[ \begin{array}{ccccc} a_{k,1}x_1 &+& a_{k,2}x_2 &=&b_k \end{array} \] signifie que le point de coordonnées \((x_1,x_2)\) est sur une droite.

Donc une paire \((x_1,x_2)\) sera solution de \((*)\), \((x_1,x_2)\in S_{(*)}\), si et seulement si le point \((x_1,x_2)\) appartient en même temps à chacune des \(m\) droites spécifiées dans \((*)\). Or appartenir à \(m\) droites en même temps est une contrainte en général difficile à satisfaire, surtout si \(m\) est grand.

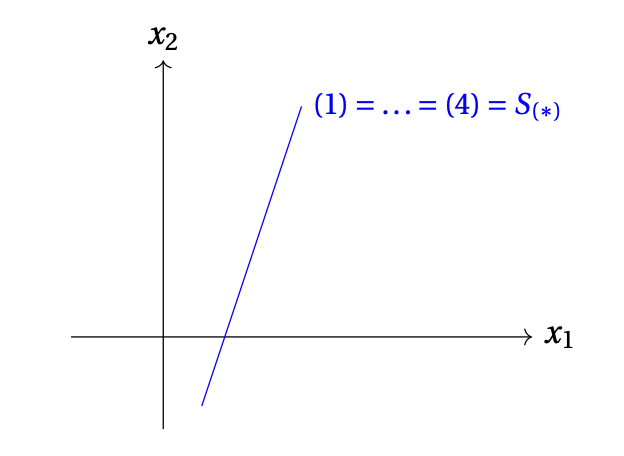
On comprend que géométriquement, il est impossible de créer \(m\) droites dans le plan qui s'intersectent, par exemple, en exactement 4 points.

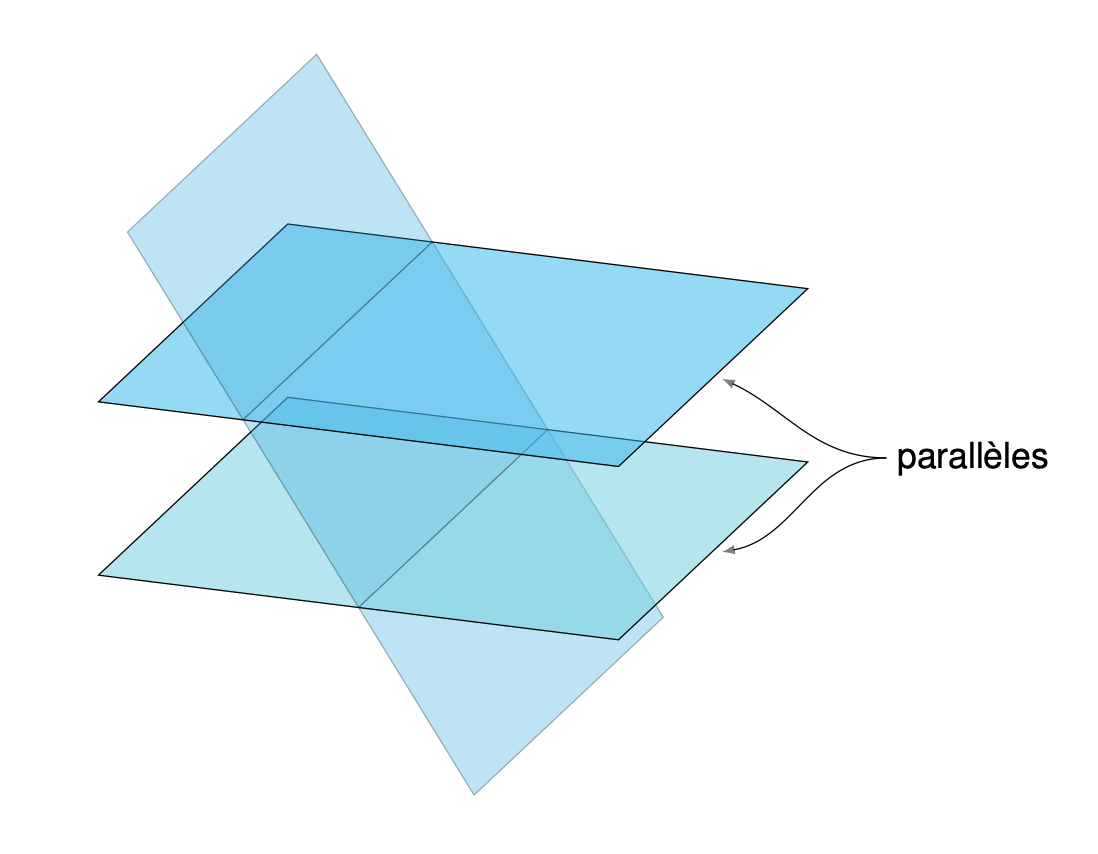
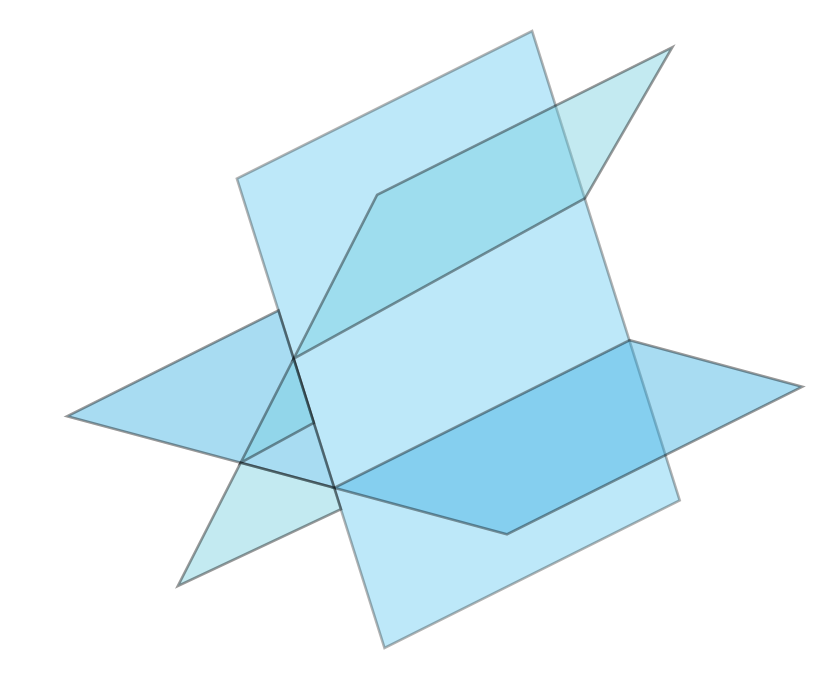
Interprétation géométrique dans le cas \(n=3\)

Fixons \(n=3\), et considérons un système de taille \(m\times 3\): \[ (*) \left\{ \begin{array}{ccccccc} a_{1,1}x_1 &+& a_{1,2}x_2 &+& a_{1,3}x_3 &=&b_1\,, \\ a_{2,1}x_1 &+& a_{2,2}x_2 &+& a_{2,3}x_3 &=&b_2\,, \\ && &&&\vdots& \\ a_{m,1}x_1 &+& a_{m,2}x_2 &+& a_{m,3}x_3 &=&b_m\,. \end{array} \right. \] Ici, un triplet \((x_1,x_2,x_3)\) peut s'interpréter comme les coordonnées d'un point dans l'espace, relativement à un repère orthonormé fixé. Aussi, on sait (voir cours de géométrie analytique) qu'une contrainte de la forme \[ \begin{array}{ccccccc} a_{k,1}x_1 &+& a_{k,2}x_2 &+& a_{k,3}x_3 &=&b_k \end{array} \] signifie que le point de coordonnées \((x_1,x_2,x_3)\) est sur un plan.

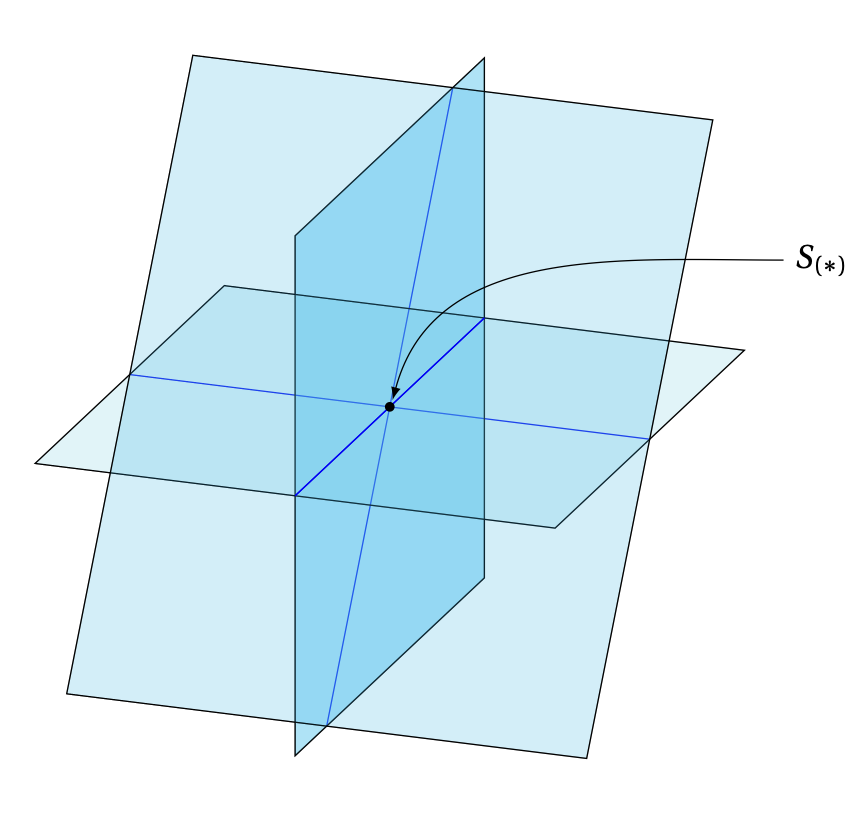
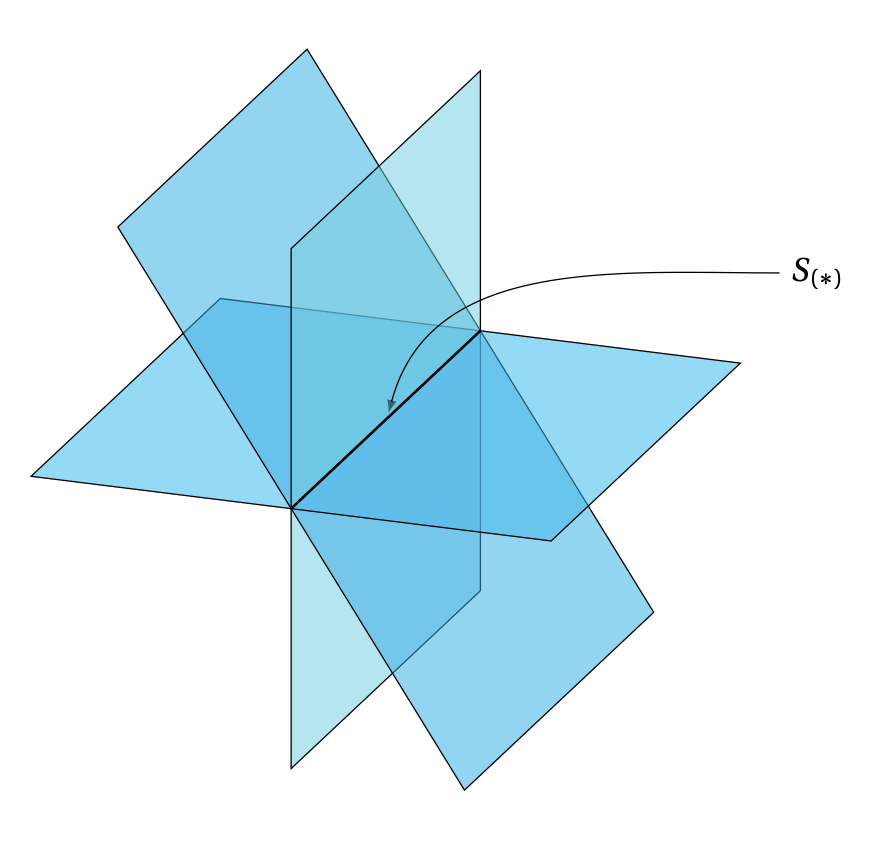
Donc un triplet \((x_1,x_2,x_3)\) sera solution de \((*)\) si et seulement si le point \((x_1,x_2,x_3)\) appartient en même temps à chacun des \(m\) plans spécifiés. Or ici aussi il est géométriquement clair que \(S_{(*)}\) ne peut contenir que \(0\), \(1\) ou une infinité de points.

Quiz 1.3-1 : Vrai ou faux?
  1. Si un système \(m\times n\) possède une infinité de solutions, et si on rajoute une équation, on obtient un système \((m+1)\times n\) qui possède aussi une infinité de solutions.
  2. Si un système \(m\times n\) possède une infinité de solutions, et si on rajoute une équation, on obtient un système \((m+1)\times n\) qui est incompatible.
  3. Si un système \(m\times n\) (\(m\geqslant 2\)) possède une infinité de solutions, et si on supprime une des \(m\) contraintes, alors on obtient un système \((m-1)\times n\) qui possède toujours une infinité de solutions.
  4. Si un système \(m\times n\) possède plus d'une solution, alors il en possède une infinité.
  5. Si un système \(m\times n\) possède moins de deux solutions, alors il est incompatible.

Dernière compilation: 2025-09-02 (09:33:29)

Sauf indication contraire, le contenu de ce document est soumis à une licence Creative Commons internationale, Attribution: Pas d'Utilisation Commerciale - Partage dans les Mêmes Conditions 4.0 (CC BY-NC-SA 4.0)