Ce premier chapitre présente les systèmes d'équations linéaires, qui seront étudiés dans ce cours.
Voyons comment les systèmes d'équations linéaires peuvent apparaître, dans des situations très pratiques. Dans une petite ville ne possédant que 4 croisements, on a mesuré les flux de voitures sur quelques axes routiers entrants et sortants de la ville, dans le but de prévoir les flux résultant sur le réseau interne, et de préparer les aménagements nécessaires:
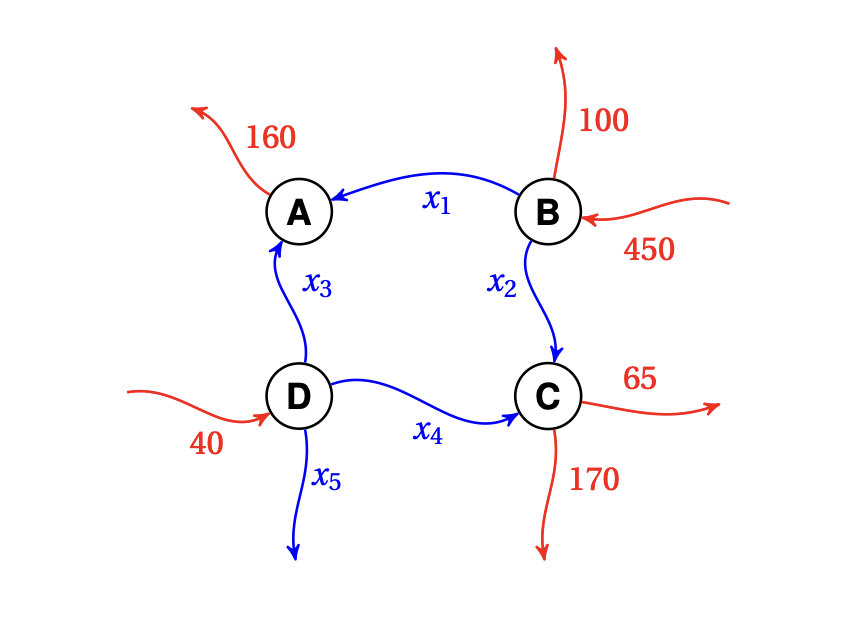
Ces mesures indiquent, par exemple, que le flux de voitures
entrant au croisement
\(B\), venant de l'est de la ville, est de \(450\) voitures par heure.
Étant données ces contraintes, se
pose la question de savoir s'il est possible de calculer les flux résultants
sur les autres
axes, indiqués par les lettres \(x_1\) à \(x_5\) sur la figure.
Le principe régissant les flux à un croisement est le même
que celui utilisé dans les réseaux électriques (Loi de Kirchhoff): en chaque
nœud du réseau, la somme des flux entrants doit être égal à la somme des flux
sortants, ce qui donne, en chacun des points du réseau,
\[\begin{aligned}
A:\quad & x_1+x_3=160\,,
\\
B:\quad & 450=100+x_1+x_2\,,
\\
C:\quad & x_2+x_4=65+170\,,
\\
D:\quad & 40=x_3+x_4+x_5\,.
\end{aligned}\]
On peut récrire ces relations comme suit:
\[
\left\{
\begin{array}{ccccccccccc}
x_1 && &+& x_3 && &&&=& 160\,,
\\
x_1 &+& x_2 && && &&&=& 350\,,
\\
&& x_2 && &+& x_4 &&&=& 235\,,
\\
&& && x_3 &+& x_4 &+& x_5 &=& 40\,.
\end{array}
\right.
\]
Plusieurs questions se posent:
Le système de \(4\) équations à \(5\) inconnues ci-dessus est un exemple de ce qu'on appelle un système d'équations linéaires ou, plus simplement, un système linéaire. Ce type de système forme une part importante de ce cours, et on commencera leur étude dans la section suivante.
Dernière compilation: 2025-09-02 (09:33:29)
Sauf indication contraire, le contenu de ce document est soumis à une licence Creative Commons internationale, Attribution: Pas d'Utilisation Commerciale - Partage dans les Mêmes Conditions 4.0 (CC BY-NC-SA 4.0)
