2.1 Vecteurs de \(\mathbb{R}^n\)
Dans ce chapitre, nous allons reformuler ce qui a été dit à propos des systèmes
en utilisant le langage vectoriel de
l'algèbre linéaire. Ceci aura plusieurs avantages, et
mènera en particulier
à une compréhension plus profonde des divers aspects liés à la recherche des
solutions d'un système linéaire.
On commence par introduire la notion de vecteur, centrale en algèbre
linéaire, et particulièrement utile pour décrire les systèmes.
On l'a déjà mentionné plus haut: toute
liste de nombres réels \((x_1,x_2,\dots, x_n)\) peut être identifiée avec un
point de l'espace \(\mathbb{R}^n\).
Sans le dire, la preuve du ''Théorème \(0,1,\infty\)'' a manipulé les points
de \(\mathbb{R}^n\) en les traitant comme des objets avec lesquels on peut faire des
calculs.
ARRANGER!
On identifiera donc \((x_1,\dots,x_n)\)
avec le vecteur (dit aussi
vecteur-colonne), noté
\[
\boldsymbol{x}=
\begin{pmatrix}
x_1\\
x_2\\
\vdots\\
x_n
\end{pmatrix}\,,
\]
qui doit s'interpréter comme le déplacement depuis l'origine jusqu'au
point de coordonnées \((x_1,x_2,\dots, x_n)\). Par exemple, dans
le plan \(\mathbb{R}^2\),
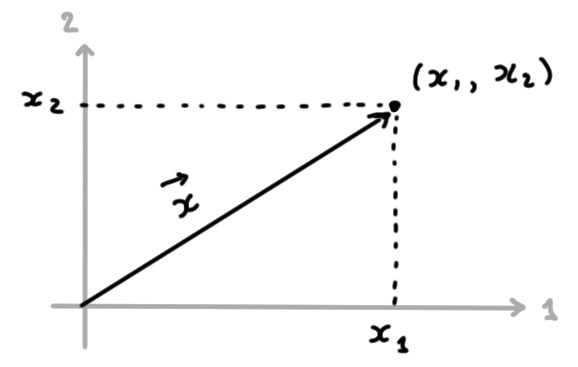 ou dans l'espace \(\mathbb{R}^3\):
ou dans l'espace \(\mathbb{R}^3\):
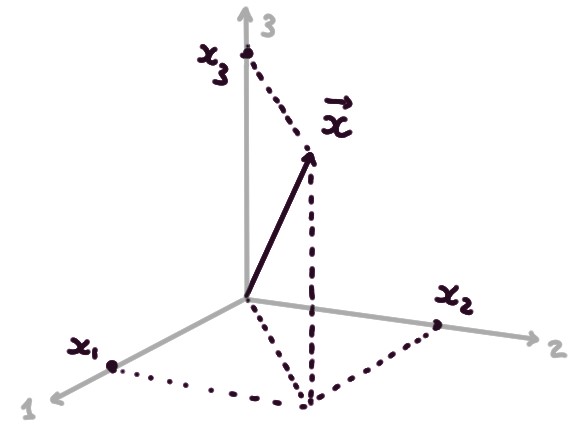 L'avantage d'identifier des points avec vecteurs est que le langage vectoriel
permet d'introduire des opérations qui rendent les vecteurs propices au
calcul.
L'avantage d'identifier des points avec vecteurs est que le langage vectoriel
permet d'introduire des opérations qui rendent les vecteurs propices au
calcul.
On munit l'ensemble des vecteurs de \(\mathbb{R}^n\) de deux opérations:
- (Multiplication par un scalaire)
La multiplication d'un vecteur
\[
\boldsymbol{x}=
\begin{pmatrix}
x_1\\
x_2\\
\vdots\\
x_n
\end{pmatrix}\,,
\]
par un scalaire \(\lambda\in \mathbb{R}\)
est le vecteur \(\lambda \boldsymbol{x}\) défini par
\[
\lambda\boldsymbol{x}:=
\begin{pmatrix}
\lambda x_1\\
\lambda x_2\\
\vdots\\
\lambda x_n
\end{pmatrix}\,.
\]
Du point de vue géométrique, la multiplication par un scalaire \(\lambda>0\)
correspond à étirer (si \(\lambda\geqslant 1\)) ou comprimer
(si \(0\lt \lambda\lt 1\)):
 Lorsque \(\lambda<0\), cette transformation est en plus accompagnée d'un
changement de sens:
Lorsque \(\lambda<0\), cette transformation est en plus accompagnée d'un
changement de sens:
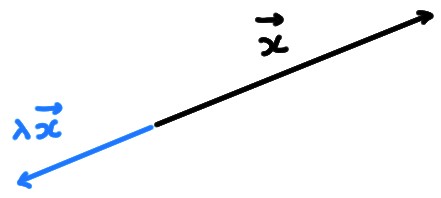
-
(Addition vectorielle)
Si deux vecteurs
\[
\boldsymbol{x}=
\begin{pmatrix}
x_1\\
x_2\\
\vdots\\
x_n
\end{pmatrix}\qquad
\text{ et }\qquad
\boldsymbol{y}=
\begin{pmatrix}
y_1\\
y_2\\
\vdots\\
y_n
\end{pmatrix}
\]
sont donnés, leur somme
est définie par
\[
\boldsymbol{x}+\boldsymbol{y}:=
\begin{pmatrix}
x_1+y_1\\
x_2+y_2\\
\vdots\\
x_n+y_n
\end{pmatrix}\,.
\]
En petites dimensions, \(n=2\) et \(n=3\), l'addition vectorielle peut
s'interpréter géométriquement comme la
règle du parallélogramme:
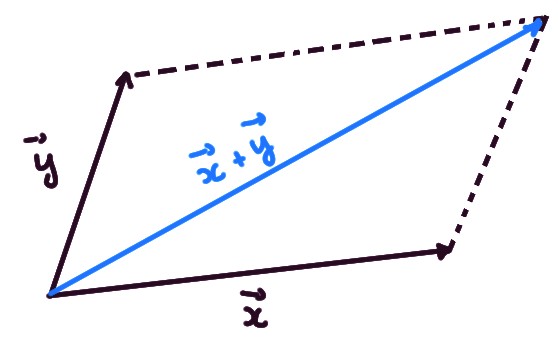
Le vecteur nul est celui dont toutes les composantes sont égales à zéro.
On le notera
\[ \boldsymbol{0}=
\begin{pmatrix}
0\\
0\\
\vdots\\
0
\end{pmatrix}\,.
\]
Par définition, on a \(0\boldsymbol{x}=\boldsymbol{0}\)
.
Pour tout vecteur
\(\boldsymbol{x}
=
\begin{pmatrix}
x_1\\
x_2\\
\vdots\\
x_n
\end{pmatrix}
\), on appelle opposé de \(\boldsymbol{x}\) le vecteur \(-\boldsymbol{x}:=
(-1)\boldsymbol{x}\). Par définition,
\[\boldsymbol{x}+(-\boldsymbol{x})=(-\boldsymbol{x})+\boldsymbol{x}=\boldsymbol{0}\,.\]
Il faut noter que
les opérations d'addition et de multiplication par un scalaire permettent
de considérer les vecteurs comme des objets avec lesquels on peut faire des calculs. Ces calculs
obéissent à certaines règles, qui sont les règles standard de l'arithmétique:
Pour tous vecteurs \(\boldsymbol{x}\), \(\boldsymbol{y}\), \(\boldsymbol{z}\) de \(\mathbb{R}^n\), et pour
tous scalaires \(\lambda,\mu\in \mathbb{R}\),
- \(\boldsymbol{x}+\boldsymbol{y}=\boldsymbol{y}+\boldsymbol{x}\) (commutativité)
- \(\boldsymbol{x}+(\boldsymbol{y}+\boldsymbol{z})= (\boldsymbol{x}+\boldsymbol{y})+\boldsymbol{z}\) (associativité)
- \(\lambda(\boldsymbol{x}+\boldsymbol{y})=\lambda\boldsymbol{y}+\lambda\boldsymbol{x}\)
- \((\lambda+\mu)\boldsymbol{x}=\lambda\boldsymbol{x}+\mu\boldsymbol{x}\)
- \((\lambda\mu)\boldsymbol{x}=\lambda(\mu\boldsymbol{x})=\mu(\lambda \boldsymbol{x})\)
Preuve:
Ces propriétés ne font que refléter une propriété élémentaire semblable, valide
dans le corps des nombres réels.
Ci-dessous, on indiquera par le symbole \(\stackrel{{\color{red}!}}{=}\)
une identité obtenue en utilisant une propriété de base dans les réels, pour
chacune des composantes:
-
\[
\boldsymbol{x}+\boldsymbol{y}
=
\begin{pmatrix}
x_1+y_1\\
x_2+y_2\\
\vdots\\
x_n+y_n
\end{pmatrix}
\stackrel{{\color{red}!}}{=}
\begin{pmatrix}
y_1+x_1\\
y_2+x_2\\
\vdots\\
y_n+x_n
\end{pmatrix}
=
\boldsymbol{y}+\boldsymbol{x}
\]
-
\[\begin{aligned}
\boldsymbol{x}+(\boldsymbol{y}+\boldsymbol{z})&=
\begin{pmatrix}
x_1\\
x_2\\
\vdots\\
x_n
\end{pmatrix}
+
\begin{pmatrix}
y_1+z_1\\
y_2+z_2\\
\vdots\\
y_n+z_n
\end{pmatrix}\\
&=
\begin{pmatrix}
x_1+(y_1+z_1)\\
x_2+(y_2+z_2)\\
\vdots\\
x_n+(y_n+z_n)
\end{pmatrix}\\
&\stackrel{{\color{red}!}}{=}
\begin{pmatrix}
(x_1+y_1)+z_1\\
(x_2+y_2)+z_2\\
\vdots\\
(x_n+y_n)+z_n
\end{pmatrix}\\
&=
\begin{pmatrix}
x_1+y_1\\
x_2+y_2\\
\vdots\\
x_n+y_n
\end{pmatrix}
+
\begin{pmatrix}
z_1\\
z_2\\
\vdots\\
z_n
\end{pmatrix}\\
&=
(\boldsymbol{x}+\boldsymbol{y})+\boldsymbol{z}
\end{aligned}\]
-
\[\begin{aligned}
\lambda(\boldsymbol{x}+\boldsymbol{y})&=
\lambda
\begin{pmatrix}
x_1+y_1\\
x_2+y_2\\
\vdots\\
x_n+y_n
\end{pmatrix}\\
&=
\begin{pmatrix}
\lambda(x_1+y_1)\\
\lambda(x_2+y_2)\\
\vdots\\
\lambda(x_n+y_n)
\end{pmatrix}\\
&\stackrel{{\color{red}!}}{=}
\begin{pmatrix}
\lambda x_1+\lambda y_1\\
\lambda x_2+\lambda y_2\\
\vdots\\
\lambda x_n+\lambda y_n
\end{pmatrix}\\
&=\lambda \boldsymbol{x}+\lambda \boldsymbol{y}
\end{aligned}\]
-
\[\begin{aligned}
(\lambda+\mu)\boldsymbol{x}&=
\begin{pmatrix}
(\lambda+\mu)x_1\\
(\lambda+\mu)x_2\\
\vdots\\
(\lambda+\mu)x_n
\end{pmatrix}\\
&\stackrel{{\color{red}!}}{=}
\begin{pmatrix}
\lambda x_1+\mu x_1\\
\lambda x_2+\mu x_2\\
\vdots\\
\lambda x_n+\mu x_n
\end{pmatrix}=\lambda \boldsymbol{x}+\mu\boldsymbol{x}
\end{aligned}\]
-
\[\begin{aligned}
(\lambda\mu)\boldsymbol{x}
&=
\begin{pmatrix}
(\lambda\mu)x_1\\
(\lambda\mu)x_2\\
\vdots\\
(\lambda\mu)x_n
\end{pmatrix}\\
&\stackrel{{\color{red}!}}{=}
\begin{pmatrix}
\lambda(\mu x_1)\\
\lambda(\mu x_2)\\
\vdots\\
\lambda(\mu x_n)
\end{pmatrix}=\lambda(\mu\boldsymbol{x})\\
&\stackrel{{\color{red}!}}{=}
\begin{pmatrix}
\mu(\lambda x_1)\\
\mu(\lambda x_2)\\
\vdots\\
\mu(\lambda x_n)
\end{pmatrix}=\mu(\lambda\boldsymbol{x})
\end{aligned}\]
Avec ces propriétés, on peut résoudre des équations vectorielles, dont
l'inconnue est un vecteur \(\boldsymbol{x}\), de la même façon qu'on
résout des équations élémentaires où l'inconnue est un réel \(x\).
Considérons deux vecteurs \(\boldsymbol{a},\boldsymbol{b}\in \mathbb{R}^n\) fixés,
et étudions l'équation vectorielle
\[
2\boldsymbol{a}-3\boldsymbol{x}=5\boldsymbol{x}+7\boldsymbol{b}\,.
\]
Utilisons les propriétés démontrées ci-dessus pour isoler \(\boldsymbol{x}\),
comme on le fait quand on résout une équation en arithmétique élémentaire.
Rajoutons \(+3\boldsymbol{x}\) des deux côtés.
Du côté gauche, détaillons l'utilisation des propriétés:
\[
2\boldsymbol{a}-3\boldsymbol{x}+3\boldsymbol{x}=2\boldsymbol{a}+(-3+3)\boldsymbol{x}=2\boldsymbol{a}+0\boldsymbol{x}=2\boldsymbol{a}
+\boldsymbol{0}=2\boldsymbol{a}\,.
\]
En procédant de même du côté droit,
on obtient
\[
2\boldsymbol{a}=8\boldsymbol{x}+7\boldsymbol{b}\,.
\]
En soustrayant \(7\boldsymbol{b}\) des deux côtés,
\[
8\boldsymbol{x}=2\boldsymbol{a}-7\boldsymbol{b}\,,
\]
puis en multipliant par \(\frac18\),
\[
\boldsymbol{x}=\tfrac14\boldsymbol{a}-\tfrac78\boldsymbol{b}\,.
\]





