La preuve est la même que dans la Section (cliquer),
mais formulée dans un langage vectoriel.
Supposons que \(S_{(*)}\) n'est pas vide, et qu'il contient plus d'un élément.
On a donc deux vecteurs \(\boldsymbol{x},\boldsymbol{y}\in \mathbb{R}^n\) distincts, tels que
\[A\boldsymbol{x}=\boldsymbol{b}\,,\qquad A\boldsymbol{y}=\boldsymbol{b}\,.\]
Considérons un scalaire \(\lambda\) quelconque, et définissons
\[\boldsymbol{z}:=\boldsymbol{y}+\lambda(\boldsymbol{x}-\boldsymbol{y})\,.\]
Si \(\lambda\) est différent de \(0\) et \(1\), alors
\(\boldsymbol{z}\) est différent de \(\boldsymbol{x}\) et de \(\boldsymbol{y}\)
.
Vérifions que \(\boldsymbol{z}\) est aussi solution de \((*)\). En effet, par la
linéarité démontrée dans le lemme,
\[
A\boldsymbol{z}=A\bigl(\boldsymbol{y}+\lambda(\boldsymbol{x}-\boldsymbol{y})\bigr)
=\underbrace{A\boldsymbol{y}}_{=\boldsymbol{b}}
+\lambda (\underbrace{A\boldsymbol{x}-A\boldsymbol{y}}_{=\boldsymbol{b}-\boldsymbol{b}=\boldsymbol{0}}
)=\boldsymbol{b}\,.
\]
On peut donc, en choisissant \(\lambda\), créer une infinité de nouvelles
solutions.
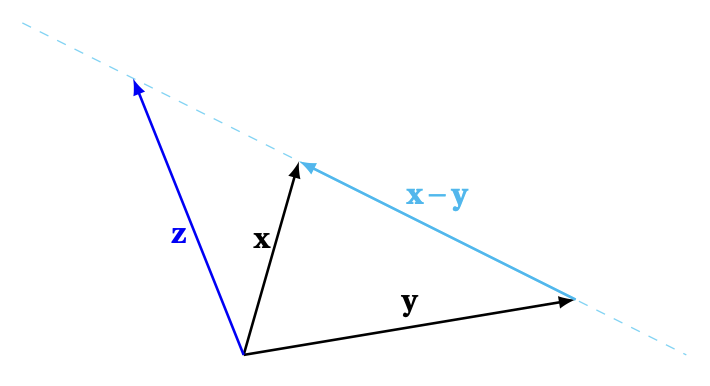
La formulation vectorielle permet d'interpréter géométriquement la
preuve donnée ci-dessus. En effet, on sait de la géométrie analytique que
le vecteur
\(\boldsymbol{z}=\boldsymbol{y}+\lambda(\boldsymbol{x}-\boldsymbol{y})\) a son extrémité située sur la
droite passant \(\boldsymbol{y}\), dirigée par \(\boldsymbol{x}-\boldsymbol{y}\):