Dans l'étude des systèmes \(m\times n\) du type \[ (*):\quad A\boldsymbol{x}=\boldsymbol{b}\,, \] il sera important de distinguer ceux dont le second membre \(\boldsymbol{b}\) est nul.
Commençons par une remarque importante: tout système homogène est compatible. En effet, il possède toujours la solution triviale , donnée par le vecteur nul \(\boldsymbol{0}\in \mathbb{R}^n\), puisque le produit d'une matrice par le vecteur nul donne toujours le vecteur nul: \[A\boldsymbol{0}=\boldsymbol{0}\,.\] (Attention, le ''\(\boldsymbol{0}\)'' du membre de gauche est le vecteur nul de \(\mathbb{R}^n\), alors que le ''\(\boldsymbol{0}\)'' du membre de droite est le vecteur nul de \(\mathbb{R}^m\)!)
Exemple: Étudions le système \(3\times 3\) homogène donné par \[ \begin{pmatrix} 1&0&2\\ 0&3&0\\ 4&0&5 \end{pmatrix} \begin{pmatrix} x_1\\ x_2\\ x_3 \end{pmatrix} = \begin{pmatrix} 0\\ 0\\ 0 \end{pmatrix}\,. \] L'opération \(L_3\leftarrow L_3-4L_1 \) donne \[ \begin{pmatrix} 1&0&2\\ 0&3&0\\ 0&0&-3 \end{pmatrix} \begin{pmatrix} x_1\\ x_2\\ x_3 \end{pmatrix} = \begin{pmatrix} 0\\ 0\\ 0 \end{pmatrix}\,, \] qui correspond au système triangulaire \[ \left\{ \begin{array}{ccccccc} x_1 && &+& 2x_3 &=&0 \\ && 3x_2 && &=&0 \\ && &-& 3x_3 &=&0 \end{array} \right.\,, \] dont l'unique solution est \((x_1,x_2,x_3)=(0,0,0)\). On conclut que dans ce cas, il n'y a pas d'autre solution que la solution triviale.
Mais un système homogène peut posséder des solutions autres que la solution triviale. En fait, dès qu'il possède une solution autre que la triviale, on sait qu'il doit en posséder une infinité.
Exemple:
Le système \(3\times 3\) homogène
\[
\begin{pmatrix}
1&1&0\\
2&8&-2\\
2&5&-1
\end{pmatrix}
\begin{pmatrix}
x_1\\ x_2\\ x_3
\end{pmatrix}
=
\begin{pmatrix}
0\\ 0\\ 0
\end{pmatrix}
\]
est équivalent à
\[
\begin{pmatrix}
1&1&0\\
0&3&-1\\
0&0&0
\end{pmatrix}
\begin{pmatrix}
x_1\\ x_2\\ x_3
\end{pmatrix}
=
\begin{pmatrix}
0\\ 0\\ 0
\end{pmatrix}\,.
\]
On voit que \(x_3\) est libre, et donc que le système possède une infinité
de solutions, décrites par
\[ S=\left\{
\begin{pmatrix}
x_1\\ x_2\\ x_3
\end{pmatrix}
=t
\begin{pmatrix}
-1\\ 1\\ 3
\end{pmatrix}
\Big|t\in \mathbb{R}
\right\}
\]
On retrouve bien-sûr la solution triviale en prenant \(t=0\), mais
toute valeur \(t\neq 0\) donne une solution non-triviale.
Remarquons encore que l'ensemble \(S\) ci-dessus n'est autre que la partie de
\(\mathbb{R}^3\) engendrée par le vecteur non-nul
\(\boldsymbol{v}=
\left(
\begin{smallmatrix}
-1\\
1\\
3
\end{smallmatrix}
\right)
\): \(S=\mathrm{Vect}\{\boldsymbol{v}\}\).
On peut donc interpréter \(S\)
comme l'ensemble de tous les vecteurs situés sur la droite
dirigée par \(\boldsymbol{v}\), passant par l'origine de \(\mathbb{R}^3\).
Exemple: Considérons le système homogène \(2\times 4\) suivant: \[ \begin{pmatrix} 1&1&1&1\\ 1&0&-1&0 \end{pmatrix} \begin{pmatrix} x_1\\ x_2\\ x_3\\ x_4 \end{pmatrix} = \begin{pmatrix} 0\\ 0 \end{pmatrix}\,. \] Deux opérations élémentaires (\(L_1\leftarrow L_1-L_2\), suivie de \(L_1\leftrightarrow L_2\)) mènent à la forme réduite \[ \begin{pmatrix} 1&0&-1&0\\ 0&1&2&1 \end{pmatrix} \begin{pmatrix} x_1\\ x_2\\ x_3\\ x_4 \end{pmatrix} = \begin{pmatrix} 0\\ 0 \end{pmatrix}\,, \] qui correspond à \[ (*) \left\{ \begin{array}{ccccccccc} x_1 && &-& x_3 && &=&0\\ &x_2& &+& 2x_3 &+&x_4 &=&0 \end{array} \right.\,, \] dans lequel \(x_3=s\) et \(x_4=t\) sont libres. On a donc \[ S= \left\{ \begin{pmatrix} x_1\\ x_2\\ x_3\\ x_4 \end{pmatrix} = \begin{pmatrix} s\\ -2s-t\\ s\\ t \end{pmatrix} \Big| s,t\in\mathbb{R} \right\} \]
Par définition, le problème de savoir si une famille
\(\{\boldsymbol{v}_1,\dots,\boldsymbol{v}_p\}\subset \mathbb{R}^n\)
est libre ou liée revient à étudier les familles de
coefficients \(\alpha_1,\dots,\alpha_p\) pour lesquelles la condition
\[
\alpha_1\boldsymbol{v}_1+\cdots+\alpha_p\boldsymbol{v}_p=\boldsymbol{0}
\]
peut être satisfaite.
D'un point de vue calculatoire, ce problème peut être reformulé comme suit.
Définissons la matrice \(n\times p\),
\[
A:= \bigl[\,\boldsymbol{v}_1\,\cdots\, \boldsymbol{v}_p\,\bigr]\,,
\]
et introduisons le vecteur
\[ \boldsymbol{\alpha}=
\begin{pmatrix}
\alpha_1\\
\vdots\\
\alpha_p
\end{pmatrix}
\in \mathbb{R}^p\,.
\]
Alors \(\{\boldsymbol{v}_1,\dots,\boldsymbol{v}_p\}\) est
libre si et seulement si le système homogène
\[
A\boldsymbol{\alpha}=\boldsymbol{0}
\]
ne possède que la solution triviale: \(\boldsymbol{\alpha}=\boldsymbol{0}\).
Exemple:
Soient
\[
\boldsymbol{v}_1=
\begin{pmatrix} 1\\ 2\\ 3 \end{pmatrix}
\,,\quad
\boldsymbol{v}_2=
\begin{pmatrix} 0\\ 1\\ -4 \end{pmatrix}
\,,\quad
\boldsymbol{v}_3=
\begin{pmatrix} 7\\ -2\\ 3 \end{pmatrix}
\,.
\]
La famille
\(\mathcal{F}=\{\boldsymbol{v}_1,\boldsymbol{v}_2,\boldsymbol{v}_3\}\subset \mathbb{R}^3\) est-elle libre ou liée?
Le système \(A\boldsymbol{\alpha}=\boldsymbol{0}\) correspondant est
\[
\begin{pmatrix}
1&0&7\\
2&1&-2\\
3&-4&3
\end{pmatrix}
\begin{pmatrix}
\alpha_1\\ \alpha_2\\ \alpha_3
\end{pmatrix}
=
\begin{pmatrix}
0\\ 0\\ 0
\end{pmatrix}\,,
\]
qui est équivalent à
\[
\begin{pmatrix}
1&0&7\\
0&1&-16\\
0&0&41
\end{pmatrix}
\begin{pmatrix}
\alpha_1\\ \alpha_2\\ \alpha_3
\end{pmatrix}
=
\begin{pmatrix}
0\\ 0\\ 0
\end{pmatrix}\,,
\]
qui ne possède que
la solution triviale. Donc \(\mathcal{F}\) est libre.
Cette façon de traiter l'indépendance linéaire permet d'énoncer un résultat général sur l'indépendance linéaire:
Théorème: Dans \(\mathbb{R}^n\), toute famille de plus de \(n\) vecteurs est liée.
Soit
\(\mathcal{F}=\{\boldsymbol{v}_1,\dots,\boldsymbol{v}_p\}\subset \mathbb{R}^n\),
avec \(p\gt n\).
On peut ranger ces vecteurs dans une matrice \(n\times p\),
qui a plus de colonnes que de lignes:
\[
A:=
[\boldsymbol{v}_1\,\dots\,\boldsymbol{v}_p]=
\left(
\begin{array}{cccc}
a_{11}&a_{12}&\cdots&a_{1p}\\
a_{21}&a_{22}&\cdots&a_{2p}\\
\vdots&\vdots&&\vdots \\
a_{n1}&a_{n2}&\cdots&a_{np}
\end{array}
\right)\,,
\]
où \(a_{ij}\), \(i=1,\dots,n\), sont les composantes du
vecteur \(\boldsymbol{v}_j\).
Maintenant, étudions la dépendance en considérant la relation linéaire
\[
\alpha_1\boldsymbol{v}_1+\cdots+\alpha_p\boldsymbol{v}_p=\boldsymbol{0}\,.
\]
Celle-ci correspond au système
\(A\boldsymbol{\alpha}=\boldsymbol{0}\), qui a pour matrice augmentée
\[
\left(
\begin{array}{cccc|c}
a_{11}&a_{12}&\cdots&a_{1p}&0\\
a_{21}&a_{22}&\cdots&a_{2p}&0\\
\vdots&\vdots&&\vdots &0\\
a_{n1}&a_{n2}&\cdots&a_{np}&0
\end{array}
\right)
\]
Puisque \(p\gt n\), sa
forme réduite doit contenir au moins une colonne ne contenant pas
de pivot, et donc le système possède au moins une variable libre.
Ceci implique, comme le second membre est nul,
qu'il existe une infinité de solutions non-triviales, et donc
que \(\mathcal{F}\) est liée.
Fixons maintenant un \(\boldsymbol{b}\in \mathbb{R}^m\) non-nul,
et considérons le système inhomogène
\[
(*):\quad A\boldsymbol{x}=\boldsymbol{b}\,.
\]
À l'opposé des systèmes homogènes (qui ont toujours au moins la solution
triviale), il n'y a aucune garantie concernant
l'existence d'une solution.
Mais pour que la discussion ci-dessous ne soit pas vide, supposons que
ce système est compatible: \(S_{(*)}\neq \varnothing\).
Notre but ci-dessous sera décrire une propriété générale de
l'ensemble \(S_{(*)}\).
Le résultat suivant va nous montrer que les solutions de ce système sont
intimement liées à celle du
système homogène associé, qui est celui avec la même matrice \(A\), mais
dans lequel on remplace
\(\boldsymbol{b}\) par \(\boldsymbol{0}\):
\[
(*)_h:\quad A\boldsymbol{x}=\boldsymbol{0}\,.
\]
Théorème: Supposons déjà connue une solution de \((*)\), que l'on nommera particulière, et que l'on notera \(\boldsymbol{v}_p\) . Alors toute autre solution de \((*)\), \(\boldsymbol{v}\in S_{(*)}\), peut s'écrire comme \[ \boldsymbol{v}=\boldsymbol{v}_p+\boldsymbol{v}_h\,, \] où \(\boldsymbol{v}_h\) est une certaine solution du problème homogène \((*)_h\) associé.
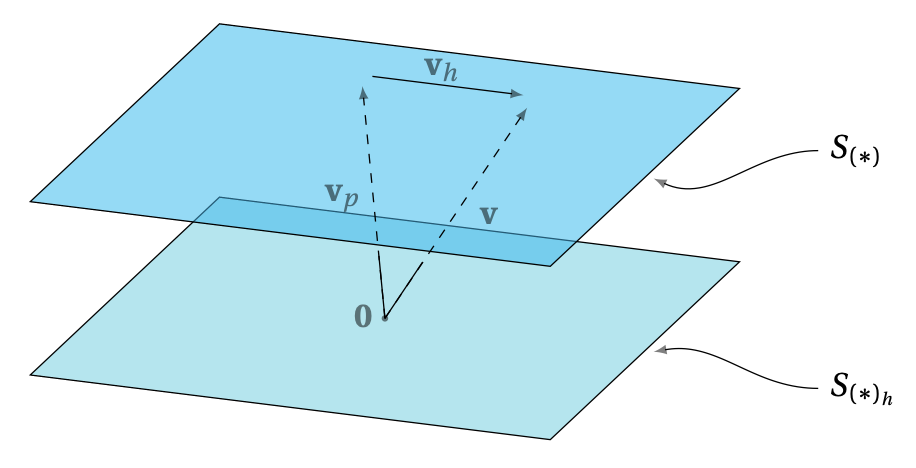
Si \(\boldsymbol{v}\in S_{(*)}\), alors \[ A\boldsymbol{v}=\boldsymbol{b}\,. \] Mais puisque \(\boldsymbol{v}_p\in S_{(*)}\), on a aussi \[ A\boldsymbol{v}_p=\boldsymbol{b}\,. \] En soustrayant ces deux dernières expressions, on obtient \[ A\boldsymbol{v}-A\boldsymbol{v}_p=\boldsymbol{b}-\boldsymbol{b}=\boldsymbol{0}\,. \] Par linéarité, ceci implique que \[ A(\boldsymbol{v}-\boldsymbol{v}_p)=\boldsymbol{0}\,. \] Ainsi, en définissant \(\boldsymbol{v}_h:= \boldsymbol{v}-\boldsymbol{v}_p\), cette dernière dit bien que \(\boldsymbol{v}_h\) est solution du problème homogène associé: \(A\boldsymbol{v}_h=\boldsymbol{0}\). Puisque \(\boldsymbol{v}=\boldsymbol{v}_p+\boldsymbol{v}_h\), ceci démontre le résultat.
Ce théorème peut être résumé comme suit: si on connaît seulement une solution du système \((*)\), et si on sait complètement résoudre le système homogène associé \((*)_h\), alors on connaît toutes les solutions du système \((*)\). Plus concrètement, pour résoudre \((*)\), on pourra procéder comme suit:
Interprétation géométrique:
Voyons comment cette structure peut s'observer sur un exemple concret.
Exemple: Considérons le système \(3\times 3\) suivant: \[ (*) \left\{ \begin{array}{ccccccc} x_1 &+& 3x_2 &+& x_3 &=& 1\\ 2x_1 &+& x_2 &-&3 x_3 &=& 7\\ -x_1 &+& 5x_2 &+&7 x_3 &=&-9 \end{array} \right. \] qui correspond à \[ A= \begin{pmatrix} 1&3&1\\ 2&1&-3\\ -1&5&7 \end{pmatrix} \,, \qquad \boldsymbol{b}= \begin{pmatrix} 1\\ 7\\ -9 \end{pmatrix}\,. \] Remarquons que le vecteur \[ \boldsymbol{v}_p:= \begin{pmatrix} 2\\ 0\\ -1 \end{pmatrix} \] est solution du système. En effet, \[ A\boldsymbol{v}_p= \begin{pmatrix} 1&3&1\\ 2&1&-3\\ -1&5&7 \end{pmatrix} \begin{pmatrix} 2\\ 0\\ -1 \end{pmatrix} = \begin{pmatrix} 1\\ 7\\ -9 \end{pmatrix}=\boldsymbol{b}\,. \] On a donc une solution particulière \(\boldsymbol{v}_p\). On sait maintenant, par le théorème, que l'on aura toutes les autres solutions en résolvant le système homogène associé, c'est-à-dire \[ (*)_h:\qquad \begin{pmatrix} 1&3&1\\ 2&1&-3\\ -1&5&7 \end{pmatrix} \begin{pmatrix} x_1\\ x_2\\ x_3 \end{pmatrix} = \begin{pmatrix} 0\\ 0\\ 0 \end{pmatrix}\,. \] En procédant comme d'habitude, on obtient \[ S_{(*)_h} = \left\{ \begin{pmatrix} x_1\\ x_2\\ x_3 \end{pmatrix} = t \begin{pmatrix} 2\\ -1\\ 1 \end{pmatrix} \,\Big|\, t\in \mathbb{R} \right\}\,. \] On sait donc, par le théorème, que toutes les solutions du problème inhomogène sont données par \[\begin{aligned} S_{(*)} &=\bigl\{\boldsymbol{v}=\boldsymbol{v}_p+\boldsymbol{v}_h\,|\,\boldsymbol{v}_h\in S_{(*)_h}\bigr\}\\ &= \left\{ \begin{pmatrix} x_1\\ x_2\\ x_3 \end{pmatrix} = \begin{pmatrix} 2\\ 0\\ -1 \end{pmatrix} +t \begin{pmatrix} 2\\ -1\\ 1 \end{pmatrix} \,\Big|\, t\in \mathbb{R} \right\}\,. \end{aligned}\] Bien-sûr, on observe cette structure aussi si on résout le système avec la technique habituelle. En partant de la matrice augmentée, \[ \left( \begin{array}{ccc|c} 1 &3 & 1 & 1\\ 2 & 1 &-3 & 7\\ -1 & 5 &7 &-9 \end{array} \right)\,, \] dont l'échelonnage mène à identifier la variable libre \(x_3=t\), on trouve \[\begin{aligned} x_1&=4+2t\,,\\ x_2&=-1-t\,,\\ x_3&=t\,. \end{aligned}\] Vectoriellement, on peut écrire l'ensemble des solutions comme \[ S_{(*)}= \left\{ \begin{pmatrix} x_1\\ x_2\\ x_3 \end{pmatrix} = \begin{pmatrix} 4\\ -1\\ 0 \end{pmatrix} +t \begin{pmatrix} 2\\ -1\\ 1 \end{pmatrix} \,\Big|\, t\in \mathbb{R} \right\} \] On voit donc encore une fois la structure ''solution particulière \(+\) toutes les solutions du problème homogène associé''.
Dernière compilation: 2023-08-30 (14:16:45)
Sauf indication contraire, le contenu de ce document est soumis à une licence Creative Commons internationale, Attribution: Pas d'Utilisation Commerciale - Partage dans les Mêmes Conditions 4.0 (CC BY-NC-SA 4.0)
