12.5 Projection sur un vecteur

La notion d'orthogonalité permet d'introduire en algèbre linéaire plusieurs notions géométriques très utiles. La première est celle de projection.

Comme motivation, fixons un vecteur \(\boldsymbol{w}\in\mathbb{R}^n\), et posons la question suivante: Pour un deuxième \(\boldsymbol{v}\in\mathbb{R}^n\) donné, comment définir la projection orthogonale de \(\boldsymbol{v}\) sur \(\boldsymbol{w}\)?

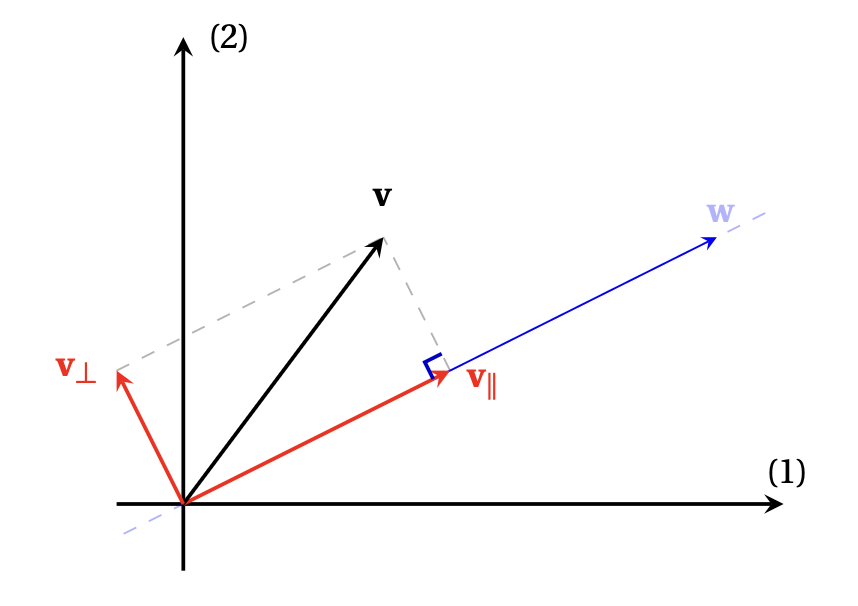
On a déjà considéré, dans le plan, la projection d'un vecteur sur une droite. Mais ici, on est en dimension quelconque \(n\)! Et nous allons commencer par projeter sur un vecteur, mais plus loin nous projetterons sur un sous-espace vectoriel quelconque de \(\mathbb{R}^n\).

Un schéma peut aider à comprendre comment nous allons procéder (attention: cette image est représentée dans le plan, mais l'argument qui suit fonctionne en toute dimension!):

La projection orthogonale de \(\boldsymbol{v}\) sur \(\boldsymbol{w}\), que nous noterons \(\boldsymbol{v}_\parallel\) pour commencer, doit permettre de décomposer \(\boldsymbol{v}\) en deux composantes vectorielles, \[ \boldsymbol{v}=\boldsymbol{v}_\parallel+\boldsymbol{v}_\perp\,, \] où

  1. \(\boldsymbol{v}_\parallel\) est colinéaire (parallèle) à \(\boldsymbol{w}\),
  2. \(\boldsymbol{v}_\perp\) est orthogonal à \(\boldsymbol{w}\).

Il se trouve que ces deux conditions caractérisent entièrement \(\boldsymbol{v}_\parallel\) et \(\boldsymbol{v}_\perp\).
En effet, pour que \(\boldsymbol{v}_\parallel\) soit colinéaire à \(\boldsymbol{w}\), il doit exister un scalaire \(\alpha\) tel que \[ \boldsymbol{v}_\parallel=\alpha\boldsymbol{w}\,. \] Puis, pour que \(\boldsymbol{v}_\perp\) soit orthogonal à \(\boldsymbol{w}\), il faut que \[ 0=\boldsymbol{v}_\perp\cdotp \boldsymbol{w} =(\boldsymbol{v}-\boldsymbol{v}_\parallel)\cdotp \boldsymbol{w} =(\boldsymbol{v}-\alpha \boldsymbol{w})\cdotp \boldsymbol{w}\,. \] De cette dernière relation, on tire que \[ \alpha =\frac{\boldsymbol{v}\cdotp\boldsymbol{w}}{\boldsymbol{w}\cdotp\boldsymbol{w}} =\frac{\boldsymbol{v}\cdotp\boldsymbol{w}}{\|\boldsymbol{w}\|^2}\,. \] En utilisant ce scalaire particulier dans \(\boldsymbol{v}_\parallel=\alpha\boldsymbol{w}\), ceci motive la définition suivante:

Soit \(\boldsymbol{w}\in \mathbb{R}^n\), \(\boldsymbol{w}\neq \boldsymbol{0}\). La projection orthogonale de \(\boldsymbol{v}\in\mathbb{R}^n\) sur \(\boldsymbol{w}\) est définie par

\[ \mathrm{proj}_{\boldsymbol{w}}(\boldsymbol{v}):= \frac{\boldsymbol{v}\cdotp\boldsymbol{w}}{\boldsymbol{w}\cdotp\boldsymbol{w}}\boldsymbol{w} =\frac{\boldsymbol{v}\cdotp\boldsymbol{w}}{\|\boldsymbol{w}\|^2}\boldsymbol{w}\,. \]

Exemple: Dans \(\mathbb{R}^5\), la projection orthogonale de \[ \boldsymbol{v}= \begin{pmatrix} 0\\2 \\-3 \\1 \\-1 \end{pmatrix}\qquad \text{ sur } \boldsymbol{w}= \begin{pmatrix} 1\\0 \\-1 \\0 \\1 \end{pmatrix} \] est donnée par \[ \mathrm{proj}_{\boldsymbol{w}}(\boldsymbol{v}) =\frac{\boldsymbol{v}\cdotp\boldsymbol{w}}{\|\boldsymbol{w}\|^2}\boldsymbol{w} =\frac{2}{3} \begin{pmatrix} 1\\0 \\-1 \\0 \\1 \end{pmatrix} = \begin{pmatrix} 2/3\\0 \\-2/3 \\0 \\2/3 \end{pmatrix} \]

Remarque: La définition de \(\mathrm{proj}_{\boldsymbol{w}}(\boldsymbol{v})\) dépend uniquement de la direction de \(\boldsymbol{w}\), pas de son sens ni de sa norme. En effet, la projection sur un vecteur colinéaire à \(\boldsymbol{w}\), \(\boldsymbol{w}'=\lambda\boldsymbol{w}\), donne le même résultat, puisque \[\begin{aligned} \mathrm{proj}_{\boldsymbol{w}'}(\boldsymbol{v}) &=\frac{\boldsymbol{v}\cdotp\boldsymbol{w}'}{\|\boldsymbol{w}'\|^2}\boldsymbol{w}'\\ &=\frac{\boldsymbol{v}\cdotp(\lambda\boldsymbol{w})}{\|\lambda\boldsymbol{w}\|^2}(\lambda\boldsymbol{w})\\ &=\frac{\boldsymbol{v}\cdotp\boldsymbol{w}}{\|\boldsymbol{w}\|^2}\boldsymbol{w}\\ &=\mathrm{proj}_{\boldsymbol{w}}(\boldsymbol{v})\,. \end{aligned}\] Donc il est plus juste de penser à la projection sur un vecteur comme à la projection sur la droite engendrée par ce vecteur.

La projection de \(\boldsymbol{v}\) sur \(\boldsymbol{w}\) est aussi optimale, dans le sens où c'est elle qui réalise la distance minimale entre \(\boldsymbol{v}\) et un vecteur quelconque de la droite dirigée par \(\boldsymbol{w}\):

Théorème: Soit \(\boldsymbol{w}\in\mathbb{R}^n\) non-nul, et soit \(W=\mathrm{Vect}\{\boldsymbol{w}\}\). Alors \[ \|\boldsymbol{v}-\mathrm{proj}_{\boldsymbol{w}}(\boldsymbol{v})\|\leqslant \|\boldsymbol{v}-\boldsymbol{x}\|\qquad \forall \boldsymbol{x}\in W\,. \] Puisque \(\mathrm{proj}_{\boldsymbol{w}}(\boldsymbol{v})\in W\), ceci implique \[ \|\boldsymbol{v}-\mathrm{proj}_{\boldsymbol{w}}(\boldsymbol{v})\|= \min_{\boldsymbol{x}\in W}\|\boldsymbol{v}-\boldsymbol{x}\|\,. \] De plus, \(\mathrm{proj}_W(\boldsymbol{v})\) est l'unique vecteur de \(W\) qui réalise ce minimum.

En d'autres termes, \(\mathrm{proj}_{\boldsymbol{w}}(\boldsymbol{v})\) est le vecteur de \(W\) dont la distance à \(\boldsymbol{v}\) est minimale:

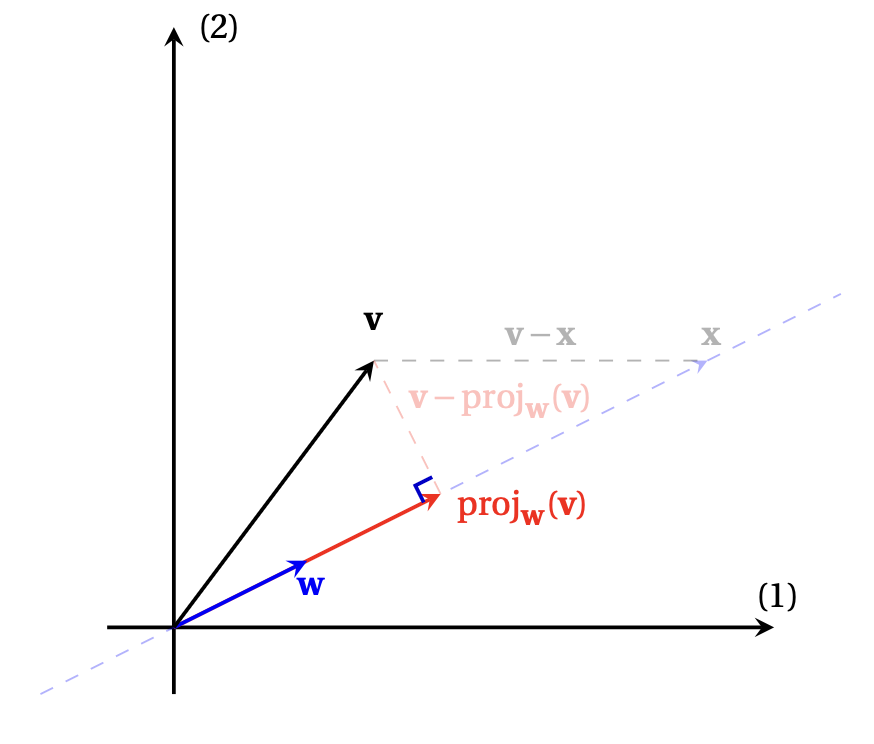
Pour tout \(\boldsymbol{x}\in W\), on peut écrire \[ \boldsymbol{v}-\boldsymbol{x}=(\underbrace{\boldsymbol{v}-\mathrm{proj}_{\boldsymbol{w}}(\boldsymbol{v})}_{\in W^\perp}) +(\underbrace{\mathrm{proj}_{\boldsymbol{w}}(\boldsymbol{v})-\boldsymbol{x}}_{\in W}) \] On a donc \[\begin{aligned} \|\boldsymbol{v}-\boldsymbol{x}\|^2 &=\|\boldsymbol{v}-\mathrm{proj}_{\boldsymbol{w}}(\boldsymbol{v})\|^2 +\underbrace{\|\mathrm{proj}_{\boldsymbol{w}}(\boldsymbol{v})-\boldsymbol{x}\|^2}_{\geqslant 0}\\ &\geqslant\|\boldsymbol{v}-\mathrm{proj}_{\boldsymbol{w}}(\boldsymbol{v})\|^2 \end{aligned}\] Supposons maintenant qu'il existe, en plus de \(\boldsymbol{v}_\parallel=\mathrm{proj}_{\boldsymbol{w}}(\boldsymbol{v})\), un autre vecteur de \(W\) satisfaisant la même propriété; notons-le \(\boldsymbol{v}_\parallel'\). Alors par définition, \[ \|\boldsymbol{v}-\boldsymbol{v}_\parallel\| =\min_{\boldsymbol{x}\in W}\|\boldsymbol{v}-\boldsymbol{x}\| = \|\boldsymbol{v}-\boldsymbol{v}_\parallel'\|\,. \] Aussi, \[\begin{aligned} \|\boldsymbol{v}-\boldsymbol{v}_\parallel'\|^2 &=\|(\underbrace{\boldsymbol{v}-\boldsymbol{v}_\parallel}_{\in W^\perp})+( \underbrace{\boldsymbol{v}_\parallel-\boldsymbol{v}_\parallel'}_{\in W})\|^2\\ &=\|\boldsymbol{v}-\boldsymbol{v}_\parallel\|^2 + \|\boldsymbol{v}_\parallel-\boldsymbol{v}_\parallel'\|^2 \end{aligned}\] On a donc \[ \|\boldsymbol{v}_\parallel-\boldsymbol{v}_\parallel'\|^2=0\,, \] qui implique \(\boldsymbol{v}_\parallel=\boldsymbol{v}_\parallel'\).

Le fait que \(\mathrm{proj}_{\boldsymbol{w}}(\boldsymbol{v})\) réalise un minimum indique que certains problèmes d'optimisation pourront trouver une solution par l'utilisation de projections. (Voir plus loin, Méthode des moindres carrés.)

Dernière compilation: 2023-08-30 (14:16:46)

Sauf indication contraire, le contenu de ce document est soumis à une licence Creative Commons internationale, Attribution: Pas d'Utilisation Commerciale - Partage dans les Mêmes Conditions 4.0 (CC BY-NC-SA 4.0)