11.8 Projection sur un sous-espace vectoriel
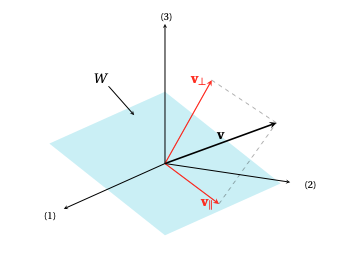
Motivation: projection sur un plan de \(\mathbb{R}^3\)
Pour motiver la définition générale de projection sur un sous-espace vectoriel
\(W\), nous commencerons par un cas légèrement plus compliqué que la projection
sur une droite (section précédente), en considérant une projection sur un plan.
Exemple:
Considérons les deux vecteurs non-colinéaires
\[
\boldsymbol{w}_1= \begin{pmatrix} 1\\1 \\-1 \end{pmatrix}\,,\qquad
\boldsymbol{w}_2= \begin{pmatrix} -2\\1 \\1 \end{pmatrix}\,,
\]
ainsi que le plan contenant l'origine, engendré par ces deux vecteurs:
\[ W=\mathrm{Vect}\{\boldsymbol{w}_1,\boldsymbol{w}_2\}\,.
\]
Si \(\boldsymbol{v}= \begin{pmatrix} 5\\ 2\\ -3 \end{pmatrix}\), comment calculer sa
projection orthogonale sur \(W\)?
Comme dans la section précédente, nous commencerons par représenter
la projection de \(\boldsymbol{v}\) sur \(W\) à l'aide du symbole
\(\boldsymbol{v}_\parallel\). Cette projection doit permettre de décomposer \(\boldsymbol{v}\)
en deux composantes vectorielles,
\[
\boldsymbol{v}=\boldsymbol{v}_\parallel+\boldsymbol{v}_\perp\,,
\]
où
- \(\boldsymbol{v}_\parallel\in W\),
- \(\boldsymbol{v}_\perp\in W^\perp\).
La première condition impose que \(\boldsymbol{v}_\parallel\)
soit une combinaison linéaire de
\(\boldsymbol{w}_1\) et \(\boldsymbol{w}_2\):
\[
\boldsymbol{v}_\parallel=\alpha_1\boldsymbol{w}_1+\alpha_2\boldsymbol{w}_2\,,
\]
et la deuxième impose que
\[
\begin{cases}
0=\boldsymbol{v}_\perp\cdotp \boldsymbol{w}_1=(\boldsymbol{v}-\alpha_1\boldsymbol{w}_1-\alpha_2\boldsymbol{w}_2)
\cdotp\boldsymbol{w}_1\,,\\
0=\boldsymbol{v}_\perp\cdotp \boldsymbol{w}_2=(\boldsymbol{v}-\alpha_1\boldsymbol{w}_1-\alpha_2\boldsymbol{w}_2)
\cdotp\boldsymbol{w}_2\,.
\end{cases}
\]
Comme \(\|\boldsymbol{w}_1\|^2=3\), \(\|\boldsymbol{w}_2\|^2=6\),
\(\boldsymbol{w}_1\cdotp\boldsymbol{w}_2=-2\),
\(\boldsymbol{v}\cdotp\boldsymbol{w}_1=10\),
\(\boldsymbol{v}\cdotp\boldsymbol{w}_2=-11\),
on en déduit que
les coefficients \(\alpha_1,\alpha_2\) sont solutions du système
\[
(*)
\left\{
\begin{array}{ccccc}
3\alpha_1 &-& 2\alpha_2 &=&10\,,\\
-2\alpha_1 &+& 6\alpha_2 &=&-11\,.
\end{array}
\right.
\]
On a donc \(\alpha_1=\frac{19}{7}\), \(\alpha_2=-\frac{13}{14}\). Ainsi, la
projection de \(\boldsymbol{v}\) sur le plan \(W\) est donnée par
\[\begin{aligned}
\boldsymbol{v}_\parallel=\frac{19}{7}\boldsymbol{w}_1-\frac{13}{14}\boldsymbol{w}_2=
\begin{pmatrix} 32/7\\ 25/14\\ -51/14 \end{pmatrix}\,.
\end{aligned}\]
Cas général
Dans le cas général, énonçons d'abord
le résultat général qui garantit que la projection
orthogonale sur un sous-espace vectoriel existe toujours:
Théorème:
Soit \(W\) un sous-espace vectoriel de \(\mathbb{R}^n\), et soit \(\boldsymbol{v}\in\mathbb{R}^n\).
Alors il existe une unique paire de vecteurs,
\(\boldsymbol{v}_\parallel\) et \(\boldsymbol{v}_\perp\), telle que
\[ \boldsymbol{v}=\boldsymbol{v}_\parallel+\boldsymbol{v}_\perp\,,
\]
et telle que
- \(\boldsymbol{v}_\parallel\in W\),
- \(\boldsymbol{v}_\perp\in W^\perp\).
Le vecteur \(\boldsymbol{v}_\parallel\) est appelé
projection orthogonale de \(\boldsymbol{v}\)
sur \(W\), et sera noté
\[\boldsymbol{v}_\parallel\equiv\mathrm{proj}_W(\boldsymbol{v})\,.\]
De plus, \(\mathrm{proj}_W(\boldsymbol{v})\) est l'unique vecteur de \(W\) qui minimise la
distance à \(\boldsymbol{v}\):
\[
\|\boldsymbol{v}-\mathrm{proj}_{W}(\boldsymbol{v})\|= \min_{\boldsymbol{x}\in W}\|\boldsymbol{v}-\boldsymbol{x}\|\,.
\]
On dit ainsi que \(\mathrm{proj}_W(\boldsymbol{v})\) donne la
meilleure approximation à
\(\boldsymbol{v}\)
avec des vecteurs de \(W\).
Dans le cas où on connaît une famille génératrice pour \(W\),
\[ W=\mathrm{Vect}\{\boldsymbol{w}_1,\dots,\boldsymbol{w}_k\}\,,
\]
on peut calculer \(\mathrm{proj}_W(\boldsymbol{v})\) comme on l'a fait dans
la section précédente, en commençant
par l'écrire comme une combinaison linéaire
\[ \boldsymbol{v}_\parallel=
\alpha_1\boldsymbol{w}_1+\cdots\alpha_k\boldsymbol{w}_k\,,
\]
où les coefficients doivent satisfaire simultanément
aux \(k\) conditions suivantes:
\[
\begin{cases}
0&=(\boldsymbol{v}-\alpha_1\boldsymbol{w}_1\cdots -\alpha_k\boldsymbol{w}_k) \cdotp\boldsymbol{w}_1\,,\\
0&=(\boldsymbol{v}-\alpha_1\boldsymbol{w}_1\cdots -\alpha_k\boldsymbol{w}_k) \cdotp\boldsymbol{w}_2\,,\\
&\vdots\\
0&=(\boldsymbol{v}-\alpha_1\boldsymbol{w}_1\cdots -\alpha_k\boldsymbol{w}_k) \cdotp\boldsymbol{w}_k\,.
\end{cases}
\]
Sans présenter de difficulté particulière,
cette approche requiert malgré tout la
résolution d'un système de taille \(n\times k\).
Cas où \(W\) est décrit par une base orthogonale
Lorsque \(W\) est décrit à l'aide d'une base orthogonale, la projection sur
\(W\) prend une forme plus explicite:
Soit \(W\) un sous-espace vectoriel de \(\mathbb{R}^n\), et soit
\(\mathcal{B}=(\boldsymbol{w}_1,\dots,\boldsymbol{w}_k)\) une base orthogonale
de \(W\).
Alors la projection orthogonale d'un vecteur \(\boldsymbol{v}\in \mathbb{R}^n\) sur \(W\)
est donnée par
\[
\mathrm{proj}_W(\boldsymbol{v})=\sum_{j=1}^k\frac{\boldsymbol{v}\cdotp
\boldsymbol{w}_j}{\|\boldsymbol{w}_j\|^2}\boldsymbol{w}_j\,.
\]
En particulier, l'application \(\boldsymbol{v}\mapsto \mathrm{proj}_W(\boldsymbol{v})\) est linéaire.
La linéarité de la projection fait qu'on peut chercher sa matrice relative à
une base.
Exemple:
Considérons les deux vecteurs non-colinéaires
\[
\boldsymbol{w}_1= \begin{pmatrix} 2\\5 \\-1 \end{pmatrix}\,,\qquad
\boldsymbol{w}_2= \begin{pmatrix} -2\\1 \\1 \end{pmatrix}\,,
\]
ainsi que le plan contenant l'origine, engendré par ces deux vecteurs:
\[ W=\mathrm{Vect}\{\boldsymbol{w}_1,\boldsymbol{w}_2\}\,.
\]
Commençons par prendre un vecteur, par exemple
\[
\boldsymbol{v}= \begin{pmatrix} 1\\ -2\\ 3 \end{pmatrix}\,,
\]
et calculons sa projection sur \(W\).
On pourrait procéder comme on l'a fait plus haut, mais on remarque tout de suite
que cette fois, \(\{\boldsymbol{w}_1,\boldsymbol{w}_2\}\) est orthogonale car
\(\boldsymbol{w}_1\cdotp\boldsymbol{w}_2=0\).
On peut donc écrire la projection directement à l'aide de la formule du
théorème:
\[\begin{aligned}
\mathrm{proj}_{W}(\boldsymbol{v})
&=
\frac{\boldsymbol{v}\cdotp\boldsymbol{w}_1}{\|\boldsymbol{w}_1\|^2}\boldsymbol{w}_1
+
\frac{\boldsymbol{v}\cdotp\boldsymbol{w}_2}{\|\boldsymbol{w}_2\|^2}\boldsymbol{w}_1\\
&=
\frac{-11}{30} \begin{pmatrix}2 \\5 \\-1 \end{pmatrix}
+
\frac{-1}{6} \begin{pmatrix} -2\\ 1\\1 \end{pmatrix}=
\begin{pmatrix}-2/5 \\-2 \\1/5 \end{pmatrix}\,.
\end{aligned}\]
Considérons ensuite la matrice de la projection, relative à la base
canonique:
\[\begin{aligned}
[\mathrm{proj}_W]_{\mathcal{B}_{\mathrm{can}}}
&=\bigl[
[\mathrm{proj}_W(\boldsymbol{e}_1)]\, [\mathrm{proj}_W(\boldsymbol{e}_2)]\, [\mathrm{proj}_W(\boldsymbol{e}_3)]
]\bigr]\\
&=
\begin{pmatrix}
4/5&0&-2/5\\
0&1&0\\
-2/5&0&1/5
\end{pmatrix}\,.
\end{aligned}\]
Cas où \(W\) est décrit par une base orthonormée
Si l'on exige en plus que la famille qui engendre \(W\) soit formée de vecteurs
unitaires, alors la projection est encore plus simple à décrire:
Soit \(W\) un sous-espace vectoriel de \(\mathbb{R}^n\), et soit
\(\mathcal{B}=\{\boldsymbol{u}_1,\dots,\boldsymbol{u}_k\}\) une base orthonormée de \(W\).
Alors la projection orthogonale d'un vecteur \(\boldsymbol{v}\in\mathbb{R}^n\) sur \(W\)
est donnée par
\[
\mathrm{proj}_W(\boldsymbol{v})=\sum_{j=1}^k(\boldsymbol{v}\cdotp
\boldsymbol{u}_j)\boldsymbol{u}_j\,.
\]
De plus, la matrice de \(\mathrm{proj}_W : \mathbb{R}^n \rightarrow \mathbb{R}^n\) (relative à la base canonique) est donnée par
\[
[\mathrm{proj}_W] = UU^T\,,
\]
où \(U\) est la matrice de taille \(n\times k\) dont les colonnes sont les vecteurs de la
base \(\mathcal{B}\) :
\[ U=\bigl[\boldsymbol{u}_1 \hskip 1mm \cdots \hskip 1mm \boldsymbol{u}_k \bigr]\,.
\]
Preuve:
Par la proposition précédente, et comme \(\|\boldsymbol{u}_j\|=1\) pour tout \(j\),
la projection est bien donnée par
\[
\mathrm{proj}_W(\boldsymbol{v})=(\boldsymbol{v}\cdotp \boldsymbol{u}_1)\boldsymbol{u}_1+
\cdots+(\boldsymbol{v}\cdotp \boldsymbol{u}_k)\boldsymbol{u}_k\,.
\]
Profitons
de la structure de cette expression pour la récrire sous forme d'un produit
matriciel:
\[\begin{aligned}
[\mathrm{proj}_W(\boldsymbol{v})]
&=(\boldsymbol{v}\cdotp\boldsymbol{u}_1) \boldsymbol{u}_1 +
\cdots+(\boldsymbol{v}\cdotp \boldsymbol{u}_k) \boldsymbol{u}_k\\
&=
\bigl[ \boldsymbol{u}_1 \hskip 1mm \cdots \hskip 1mm \boldsymbol{u}_k \bigr]
\begin{pmatrix}
\boldsymbol{v}\cdotp\boldsymbol{u}_1\\
\vdots\\
\boldsymbol{v}\cdotp\boldsymbol{u}_k
\end{pmatrix}\\
&=
\bigl[ \boldsymbol{u}_1 \hskip 1mm \cdots \hskip 1mm \boldsymbol{u}_k \bigr]
\begin{pmatrix}
\boldsymbol{u}_1^T \boldsymbol{v}\\
\vdots\\
\boldsymbol{u}_k^T \boldsymbol{v}
\end{pmatrix}\\
&=
\underbrace{\bigl[ \boldsymbol{u}_1 \hskip 1mm \cdots \hskip 1mm \boldsymbol{u}_k
\bigr]}_{=:U}
\underbrace{
\begin{bmatrix}
\boldsymbol{u}_1^T\\
\vdots\\
\boldsymbol{u}_k^T
\end{bmatrix}
}_{=U^T}
\boldsymbol{v}\,.
\end{aligned}\]
Remarque:
La projection est une application de \(\mathbb{R}^n\) dans \(\mathbb{R}^n\), donc la matrice
qui la représente est de taille \(n\times n\).
C'est bien le cas ici puisque
\[
[\mathrm{proj}_W] =
\underbrace{\underbrace{U}_{n\times k}
\,
\underbrace{U^T}_{k\times n}}_{n\times n}\,.
\]
Exemple:
Considérons la même projection orthogonale que celle vue plus haut,
sur le plan \(W\) engendré par
\[
\boldsymbol{w}_1= \begin{pmatrix} 2\\5 \\-1 \end{pmatrix}\,,\qquad
\boldsymbol{w}_2= \begin{pmatrix} -2\\1 \\1 \end{pmatrix}\,,
\]
On sait que la base
\[\mathcal{B}=\{\boldsymbol{w}_1,\boldsymbol{w}_2\}\]
est orthogonale, et on peut
la rendre orthonormée en divisant chaque vecteur par sa norme:
\[
\mathcal{B}'=\left\{
\frac{\boldsymbol{w}_1}{\|\boldsymbol{w}_1\|},\frac{\boldsymbol{w}_2}{\|\boldsymbol{w}_2\|}
\right\}\,.
\]
On peut maintenant utiliser le porisme pour obtenir
la matrice de la projection sur \(W\) relative à la base
canonique:
\[\begin{aligned}
[\mathrm{proj}_W]_{\mathcal{B}_{\mathrm{can}}}
&=\underbrace{U}_{3\times 2} \, \underbrace{U^T}_{2\times 3}\\
&=
\Bigl[
\frac{\boldsymbol{w}_1}{\|\boldsymbol{w}_1\|}\,\,\frac{\boldsymbol{w}_2}{\|\boldsymbol{w}_2\|}
\Bigr]
\begin{bmatrix}
\frac{\boldsymbol{w}_1^T}{\|\boldsymbol{w}_1\|} \\
\frac{\boldsymbol{w}_2^T}{\|\boldsymbol{w}_2\|}
\end{bmatrix}\\
&=
\begin{pmatrix}
2/\sqrt{30}&-2/\sqrt{6}\\
5/\sqrt{30}&1/\sqrt{6}\\
-1/\sqrt{30}&1/\sqrt{6}
\end{pmatrix}
\begin{pmatrix}
2/\sqrt{30}&5/\sqrt{30}&-1/\sqrt{30}\\
-2/\sqrt{6}&1/\sqrt{6}&1/\sqrt{6}
\end{pmatrix}\\
&=
\begin{pmatrix}
4/5&0&-2/5\\
0&1&0\\
-2/5&0&1/5
\end{pmatrix}\,,
\end{aligned}\]
qui est bien la même que nous avions trouvé plus haut.
On peut maintenant utiliser cette matrice pour projeter n'importe quel vecteur
sur \(W\).
Par exemple,
\[\begin{aligned}
\mathrm{proj}_W
\begin{pmatrix} 1\\ -2\\ 3 \end{pmatrix}
&=
\begin{pmatrix}
4/5&0&-2/5\\
0&1&0\\
-2/5&0&1/5
\end{pmatrix}
\begin{pmatrix} 1\\ -2\\ 3 \end{pmatrix}=
\begin{pmatrix} -2/5\\ -2\\1/5 \end{pmatrix}\,.
\end{aligned}\]
Exemple:
Considérons la projection \(\mathrm{proj}_d\)
sur une droite \(d\) passant par l'origine et faisant
un angle de \(\theta\) avec \(\boldsymbol{e}_1\):
Cette droite \(d\) est un sous-espace de \(\mathbb{R}^2\), engendrée par le vecteur unitaire
\[ \boldsymbol{u}_1= \begin{pmatrix} \cos\theta\\ \sin\theta \end{pmatrix}\,. \]
Par la formule du porisme ci-dessus, sa matrice relative à la base
canonique est donc donnée par
\[\begin{aligned}
[\mathrm{proj}_d]
&=UU^T\\
&=\boldsymbol{u}_1\boldsymbol{u}_1^T\\
&=
\begin{pmatrix} \cos\theta\\ \sin\theta \end{pmatrix}
\begin{pmatrix}
\cos\theta&\sin\theta
\end{pmatrix}\\
&=
\begin{pmatrix}
\cos^2\theta&\cos\theta\sin\theta\\
\cos\theta\sin\theta&\sin^2\theta
\end{pmatrix}\,.
\end{aligned}\]
Remarque:
Il est important d'apprécier
l'ordre des matrices apparaissant dans la formule
\[
[\mathrm{proj}_W]=UU^T\,.
\]
Le fait que les matrices soient dans cet ordre (''\(U\) fois \(U^T\)'') font de
leur produit une application linéaire non-triviale, qui projette sur l'espace
engendré par les colonnes de \(U\).
Car si
l'on multiplie ces matrices dans l'ordre inverse, on obtient une matrice de taille \(k\times
k\) contenant les produits scalaires
\[
\boldsymbol{u}_i^T\boldsymbol{u}_j=\boldsymbol{u}_i\cdotp \boldsymbol{u}_j=
\begin{cases}
\|\boldsymbol{u}_i\|=1\,,&\text{ si }i=j\,,\\
0\,,&\text{ sinon,}
\end{cases}
\]
et donc
\[\begin{aligned}
U^TU
&=
\begin{pmatrix}
\boldsymbol{u}_1\cdotp\boldsymbol{u}_1&\boldsymbol{u}_1\cdotp\boldsymbol{u}_2&\cdots&\boldsymbol{u}_1\cdotp\boldsymbol{u}_k\\
\boldsymbol{u}_2\cdotp\boldsymbol{u}_1&\boldsymbol{u}_2\cdotp\boldsymbol{u}_2&\cdots&\boldsymbol{u}_2\cdotp\boldsymbol{u}_k\\
\vdots&\vdots&\ddots&\vdots\\
\boldsymbol{u}_k\cdotp\boldsymbol{u}_1&\boldsymbol{u}_k\cdotp\boldsymbol{u}_2&\cdots&\boldsymbol{u}_k\cdotp\boldsymbol{u}_k
\end{pmatrix}\\
&=
\begin{pmatrix}
\|\boldsymbol{u}_1\|^2&0&\cdots&0\\
0&\|\boldsymbol{u}_2\|^2&\cdots&0\\
\vdots&\vdots&\ddots&\vdots\\
0&0&\cdots&\|\boldsymbol{u}_k\|^2
\end{pmatrix}\\
&=I_k\,.
\end{aligned}\]