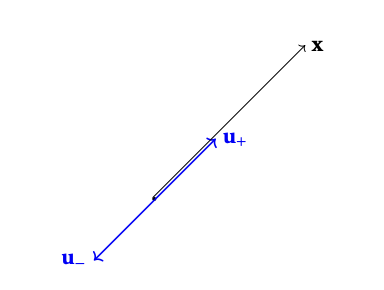
Remarque: Pour tout vecteur non-nul \(\boldsymbol{x}\), il existe exactement deux vecteurs unitaires qui sont colinéaires à \(\boldsymbol{x}\), donnés par \[ \boldsymbol{u}_\pm := \pm \frac{\boldsymbol{x}}{\|\boldsymbol{x}\|}\,. \]
Pour la première propriété,
\[\begin{aligned}
\|\lambda\boldsymbol{x}\|
&=\sqrt{(\lambda x_1)^2+\dots+(\lambda x_n)^2}\\
&=\sqrt{\lambda^2 x_1^2+\dots+\lambda^2 x_n^2}\\
&=\sqrt{\lambda^2(x_1^2+\dots+x_n^2)}\\
&=|\lambda|\sqrt{x_1^2+\dots+x_n^2}\\
&=|\lambda|\|\boldsymbol{x}\|\,.
\end{aligned}\]
Ensuite, \(\|\boldsymbol{x}\|\geqslant 0\) est évidente, et remarquons que \(\|\boldsymbol{x}\|=0\)
si et seulement si \(\|\boldsymbol{x}\|^2=0\), qui est équivalente à
\[ x_1^2+\cdots +x_n^2=0\,.
\]
Or une somme de nombres non-négatifs est nulle si et seulement chacun de ces
nombres est nul, \(x_k^2=0\), et donc \(x_k=0\) pour chaque \(k=1,\dots,n\).
On démontrera l'inégalité triangulaire dans la section suivante.
Remarque: Pour tout vecteur non-nul \(\boldsymbol{x}\), il existe exactement deux vecteurs unitaires qui sont colinéaires à \(\boldsymbol{x}\), donnés par \[ \boldsymbol{u}_\pm := \pm \frac{\boldsymbol{x}}{\|\boldsymbol{x}\|}\,. \]

La notion de norme permet de définir encore deux notions géométriques classiques: