Dans ce chapitre on va étudier la notion de distance entre vecteurs, et entre vecteurs et sous-espaces vectoriels. Pour le faire on va introduire la notion de produit scalaire des vecteurs, qui nous permet aussi d'étudier la notion d'orthogonalité (aussi appelé perpendicularité).
La raison fondamentale pour laquelle on s'intéresse aux notions de distance et de perpendicularité est due au problème suivant. Souvent on va se rencontrer avec des système d'équations linéaires \(A \boldsymbol{x} = \boldsymbol{b}\), où \(A\) est une matrice de taille \(m \times n\) et \(\boldsymbol{b} \in \mathbb{R}^m\), qui sont incompatibles, i.e. qui n'ont pas de solution. Jusqu'à maintenant, on s'est contenté de dire uniquement qu'ils n'admettent pas de solution. Par contre, même si ces systèmes d'équations linéaires n'ont pas de solution au sens strict, on peut considérer des points qui sont les plus proches à être une solution, i.e. des éléments \(\boldsymbol{x}_0 \in \mathbb{R}^n\) tels que \[ \text{distance entre } A \boldsymbol{x}_0 \text{ et } \boldsymbol{b} \text{ soit minimale. } \] On verra les détails de ces calculs, et en particulier comment calculer les vecteurs qui minimisent la distance précédente dans le chapitre suivant. La perpendicularité rentre dans ce problème, car, comme on verra plus tard, la condition de minimalité de la distance précédente est équivalente au fait que \( \boldsymbol{b} - A\boldsymbol{x}_0 \) est orthogonal à tout vecteur de la image \(\mathrm{Im} (A)\) de \(A\).
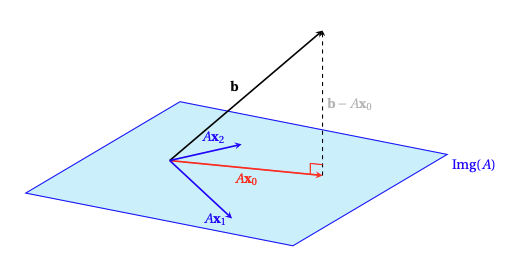
La situation peut se représenter graphiquement de la façon suivante :
Dernière compilation: 2025-09-02 (09:33:30)
Sauf indication contraire, le contenu de ce document est soumis à une licence Creative Commons internationale, Attribution: Pas d'Utilisation Commerciale - Partage dans les Mêmes Conditions 4.0 (CC BY-NC-SA 4.0)
