Dans cette section, nous allons introduire la notion de produit scalaire sur un espace vectoriel quelconque. Ceci permettra de définir la notion de perpendicularité dans un cadre très général, et d'utiliser une approche semblable à celle des derniers chapitres pour la résolution de nombreux problèmes d'approximation.
Exemple: L'espace \(\mathbb{R}^n\), muni du produit scalaire euclidien \[ (\boldsymbol{u}|\boldsymbol{v}):= \boldsymbol{u}\cdotp\boldsymbol{v} =u_1v_1+\cdots+u_nv_n\,, \] est notre premier exemple d'espace euclidien.
Exemple: On considère l'espace vectoriel \( V = \mathbb{R}^2\) muni du produit scalaire donné par \[ (\boldsymbol{u}|\boldsymbol{v}) := \boldsymbol{u}^T \begin{pmatrix} 3 & 1 \\ 1 & 3 \end{pmatrix} \boldsymbol{v} = 3 u_1 v_1 + u_1 v_2 + u_2 v_1 + 3 u_2 v_2\,. \] L'expression précédent définie en effet un produit scalaire. La symétrie suit de \[ (\boldsymbol{u}|\boldsymbol{v}) = 3 u_1 v_1 + u_1 v_2 + u_2 v_1 + 3 u_2 v_2 = 3 v_1 u_1 + v_1 u_2 + v_2 u_1 + 3 v_2 u_2 = (\boldsymbol{v}|\boldsymbol{u}) \] et la bilinéarité suit de \[\begin{aligned} (\boldsymbol{u}+\lambda \boldsymbol{u}'|\boldsymbol{v}) &= 3 (u_1 + \lambda u'_1) v_1 + (u_1 + \lambda u'_1) v_2 + (u_2 + \lambda u'_2) v_1 + 3 (u_2 + \lambda u'_2) v_2 \\ &= (3 u_1 v_1 + u_1 v_2 + u_2 v_1 + 3 u_2 v_2) + \lambda (3 u'_1 v_1 + u'_1 v_2 + u'_2 v_1 + 3 u'_2 v_2) = (\boldsymbol{u}|\boldsymbol{v}) +\lambda (\boldsymbol{u}'|\boldsymbol{v}). \end{aligned}\] Finalement, on note que \[ (\boldsymbol{u}|\boldsymbol{u}) = 3 u_1^2 + 2 u_1 u_2 + 3 u_2^2 = 2(u_1^2+u_2^2) + (u_1+u_2)^2 \geqslant 0, \] et l'égalité est vraie si et seulement si \(u_1^2 = u_2^2 = (u_1+u_2)^2 = 0\), u.e. \(u_1=u_2=0\), ce qui équivaut à \(\boldsymbol{u} = \boldsymbol{0}\).
Exemple: Sur l'espace vectoriel des polynômes \(\mathbb{P}_{n}\), on peut vérifier que \[ (p|q):= \sum_{i=0}^n p(i) q(i) \] définit un produit scalaire. En effet, la symétrie et la bilinéarité sont clairement satisfaites, et \[ (p|p)= \sum_{i=0}^n p(i)^2\geqslant 0\,, \] et cette somme de carrés est nulle si et seulement chacun des carrés \(p(i)^2=0\), c'est-à-dire \(p(i)=0\), et donc \(p=\mathbf{0}\) est le polynôme nul, vu que l'unique polynôme de degré inférieur ou égal à \(n\) avec \(n+1\) racines différentes est le polynôme nul.
Exemple: Sur l'espace vectoriel des matrices \(\mathbb{M}_{m\times n}(\mathbb{R})\), on peut vérifier que \[ (A|B):= \sum_{i=1}^m\sum_{j=1}^n A_{i,j} B_{i,j} \] définit un produit scalaire. En effet, la symétrie et la bilinéarité sont clairement satisfaites, et \[ (A|A)= \sum_{i=1}^m\sum_{j=1}^n A_{i,j}^2\geqslant 0\,, \] et cette somme de carrés est nulle si et seulement chacun des carrés \(A_{i,j}^2=0\), c'est-à-dire \(A_{i,j}=0\), et donc \(A=\mathbf{0}\) est la matrice nulle.
Si \(V\) est muni d'un produit scalaire \((\cdot|\cdot)\), on peut maintenant définir
Considérons l'espace vectoriel de toutes les fonctions continues sur un
intervalle fermé et borné, \(f:[a,b]\to\mathbb{R}\), noté \(C([a,b])\).
Notons (voir le cours d') que les fonctions continues sont intégrables.
Donc si \(f,g\in C([a,b])\), leur produit étant aussi une fonction continue,
on peut définir le nombre
\[
(f|g):=
\int_a^bf(t)g(t)\,dt\,.
\]
Lemme: Cette expression définit un produit scalaire sur \(C([a,b])\).
D'abord, \[(f|g)= \int_a^b f(t)g(t)\,dt= \int_a^b g(t)f(t)\,dt=(g|f)\,.\] Ensuite, si on fixe \(g\), alors pour tous \(f_1,f_2\in C([a,b])\), \(\lambda_1,\lambda_2\in\mathbb{R}\), les propriétés de linéarité de l'intégrale impliquent \[\begin{aligned} (\lambda_1f_1+\lambda_2f_2|g)&= \int_a^b\big(\lambda_1f_1(t)+\lambda_2f_2(t)\big)g(t)\,dt\\ &= \lambda_1\int_a^b f_1(t)g(t)\,dt+ \lambda_2\int_a^b f_2(t)g(t)\,dt\\ &= \lambda_1(f_1|g)+ \lambda_2(f_2|g)\,. \end{aligned}\] En utilisant la symétrie (première propriété), et la propriété précédente, \[\begin{aligned} (f\,|\,\lambda_1g_1+\lambda_2g_2) &=(\lambda_1g_1+\lambda_2g_2\,|\,f)\\ &=\lambda_1(g_1\,|\,f)+\lambda_2(g_2\,|\,f)\\ &=\lambda_1(f\,|\,g_1)+\lambda_2(f\,|\,g_2)\,. \end{aligned}\] Puisque l'intégrale d'une fonction non-négative est non-négative, \[ (f|f)=\int_a^b\underbrace{f(t)^2}_{\geqslant 0}\,dt\geqslant 0\,. \] De plus, l'intégrale de \(f(t)^2\) est nulle si et seulement si \(f(t)=0\) pour tout \(t\in [a,b]\) (voir le cours d'), ce qui implique que \(f\) est la fonction identiquement nulle: \(f=0\).
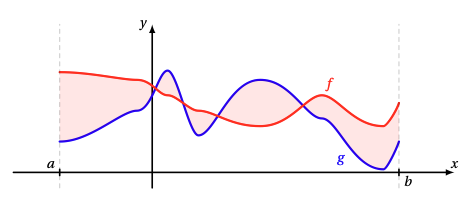
Ainsi, muni de ce produit scalaire, \(C([a,b])\) est un espace préhilbertien (mais pas euclidien puisque \(C([a,b])\) est de dimension infinie). En particulier:
Intuitivement, deux fonctions \(f,g\) continues sur \([a,b]\) sont proches, au sens de \(\|\cdot\|\), si l'aire géométrique qui sépare leurs graphes est petite:
(Malgré tout, ce n'est pas exactement cette aire qui apparaît puisqu'on intègre
le carré \(|f(t)-g(t)|^2\).)
L'interprétation du produit scalaire, par contre, est moins évidente.
Exemple: Sur \(C([0,\pi])\), considérons les fonctions \(f(t):= t\) et \(g(t):= \sin(t)\), et calculons leur produit scalaire en utilisant une intégration par parties: \[\begin{aligned} (f|g) &=\int_0^\pi t\sin(t)\,dt\\ &=t\big(-\cos(t)\big)\Big|_0^\pi+\int_0^\pi\cos(t)\,dt=\pi\,. \end{aligned}\] Ensuite, si \(h(t)=\cos(t)\), alors \[\begin{aligned} (g|h)&=\int_0^\pi\sin(t)\cos(t)\,dt\\ &=\frac12\int_0^\pi\sin(2t)\,dt\\ &=\frac14\big(-\cos(2t)\big)\Big|_0^\pi=0\,, \end{aligned}\] donc \(g\perp h\).
Dernière compilation: 2025-09-02 (09:33:30)
Sauf indication contraire, le contenu de ce document est soumis à une licence Creative Commons internationale, Attribution: Pas d'Utilisation Commerciale - Partage dans les Mêmes Conditions 4.0 (CC BY-NC-SA 4.0)
