Remarque: Il sera souvent utile de récrire le produit scalaire euclidien en le réinterprétant comme un produit matriciel un peu particulier: \[ \boldsymbol{x}\cdotp\boldsymbol{y}= x_1y_1+\dots+x_ny_n= \underbrace{(x_1\cdots x_n)}_{1\times n} \underbrace{ \begin{pmatrix} y_1\\ \vdots\\ y_n \end{pmatrix} }_{n\times 1} =\boldsymbol{x}^T\boldsymbol{y}\,. \]
Les cinq premières propriétés suivent directement de la définition du produit
scalaire euclidien.
Démontrons l'inégalité de Cauchy-Schwarz.
Pour commencer, remarquons que l'inégalité est triviale dès que \(\boldsymbol{y}\) (ou
\(\boldsymbol{x}\)) est nul. On peut donc supposer que \(\boldsymbol{y}\neq \boldsymbol{0}\).
Ensuite, remarquons que pour tout \(t \in\mathbb{R}\),
\[\begin{aligned}
0\leqslant \|\boldsymbol{x}+t \boldsymbol{y}\|^2
&=(\boldsymbol{x}+t \boldsymbol{y})\cdotp(\boldsymbol{x}+t \boldsymbol{y})\\
&=\boldsymbol{x}\cdotp
\boldsymbol{x}+2t (\boldsymbol{x}\cdotp\boldsymbol{y})+t ^2(\boldsymbol{y}\cdotp\boldsymbol{y})\\
&=\|\boldsymbol{x}\|^2
+2t (\boldsymbol{x}\cdotp\boldsymbol{y})+t ^2\|\boldsymbol{y}\|^2\,.\\
\end{aligned}\]
Comme cette inégalité est vraie pour tout \(t \in \mathbb{R}\), le discriminant du polynôme quadratique précédent est non positif, vu qu'il possède au moins une racine réelle, ce qui implique que
\[ 4 (\boldsymbol{x}\cdotp\boldsymbol{y})^2 - 4 \|\boldsymbol{x}\|^2\|\boldsymbol{y}\|^2 \leqslant 0\,, \]
ce qui équivaut à
\[ (\boldsymbol{x}\cdotp\boldsymbol{y})^2\leqslant \|\boldsymbol{x}\|^2\|\boldsymbol{y}\|^2\,.
\]
On obtient l'inégalité de Cauchy-Schwarz en prenant la racine carrée des deux
côtés.
Remarque: \(\mathbb{R}^n\), muni du produit scalaire, est un cas particulier de ce que nous appellerons plus tard un espace euclidien.
On peut utiliser l'inégalité de Cauchy-Schwarz pour démontrer l'inégalité triangulaire de la section précédente: \[\begin{aligned} \|\boldsymbol{x}+\boldsymbol{y}\|^2 &=(\boldsymbol{x}+\boldsymbol{y})\cdotp(\boldsymbol{x}+\boldsymbol{y})\\ &=\|\boldsymbol{x}\|^2+2(\boldsymbol{x}\cdotp\boldsymbol{y})+\|\boldsymbol{y}\|^2\\ &\leqslant \|\boldsymbol{x}\|^2+2\|\boldsymbol{x}\|\|\boldsymbol{y}\|+\|\boldsymbol{y}\|^2\\ &=\big(\|\boldsymbol{x}\|+\|\boldsymbol{y}\|\big)^2\,. \end{aligned}\]
Le produit scalaire est surtout utilisé, en algèbre linéaire, pour résoudre des problèmes dans \(\mathbb{R}^n\) à l'aide d'arguments géométriques empruntés à la géométrie du plan et de l'espace. Et la première notion qui joue un rôle en géométrie est celle d'orthogonalité.
Exemple: Dans \(\mathbb{R}^5\), les vecteurs \[ \boldsymbol{x}= \begin{pmatrix} 3\\ 1\\ -2\\ 0\\ 2 \end{pmatrix}\,,\qquad \boldsymbol{y}= \begin{pmatrix} 2\\ 2\\ 5\\ 3\\ 1 \end{pmatrix}\, \] sont orthogonaux, vu que \(\boldsymbol{x}\cdotp\boldsymbol{y}=0\).
Voici une description équivalente de l'orthogonalité de vecteurs de \(\mathbb{R}^n\):
Lemme: Deux vecteurs \(\boldsymbol{x},\boldsymbol{y}\in\mathbb{R}^n\) sont orthogonaux si et seulement si \(\|\boldsymbol{x}+\boldsymbol{y}\|^2=\|\boldsymbol{x}\|^2 +\|\boldsymbol{y}\|^2\).
On remarque d'abord l'égalité \[ (\boldsymbol{x}\cdotp\boldsymbol{y})= \frac12 \Big( \|\boldsymbol{x}+\boldsymbol{y}\|^2 -\big(\|\boldsymbol{x}\|^2 +\|\boldsymbol{y}\|^2\big) \Big)\,. \] Ceci implique que \(\boldsymbol{x}\cdotp \boldsymbol{y}=0\) si et seulement si \(\|\boldsymbol{x}+\boldsymbol{y}\|^2=\|\boldsymbol{x}\|^2 + \|\boldsymbol{y}\|^2\), comme on voulait démontrer.
En géométrie, on considère souvent un objet géométrique, généralement une droite ou un plan, défini comme étant perpendiculaire à un autre. En algèbre linéaire, on définit un ensemble de vecteurs qui sont tous orthogonaux aux vecteurs d'un autre ensemble:
Commençons par comprendre intuitivement le sens de \(W^\perp\), en petites dimensions:
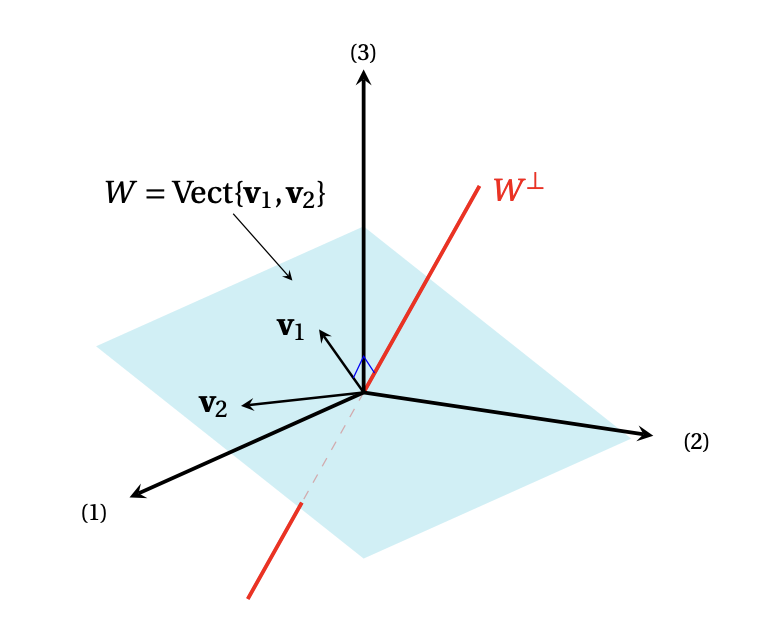
Exemple: Si \(W\) est un plan (passant par l'origine) de \(\mathbb{R}^3\), alors \(W^\perp\) est la droite perpendiculaire à \(W\), passant par l'origine:
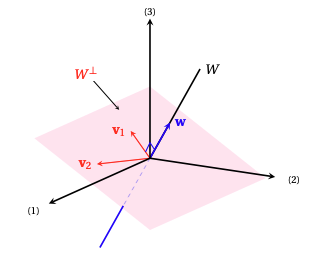
Exemple: Si \(W\) est une droite (passant par l'origine) de \(\mathbb{R}^3\), alors \(W^\perp\) est le plan perpendiculaire à \(W\), passant par l'origine:
Ces deux derniers exemples illustrent bien les propriétés générales ci-dessous:
On vérifie que \(W^\perp\) est un sous-espace vectoriel de \(\mathbb{R}^n\).
Dans la définition, \(W^\perp\) est défini comme l'ensemble des vecteurs qui sont orthogonaux à tous les vecteurs de \(W\). Ceci implique que d'un point de vue calculatoire, on devrait a priori vérifier une infinité de conditions pour savoir si un vecteur appartient à \(W^\perp\). Mais lorsqu'on possède une base les choses sont plus simples:
Lemme: Soit \(W\) un sous-espace vectoriel de \(\mathbb{R}^n\), et soit \(\mathcal{B}=\{\boldsymbol{w}_1,\dots,\boldsymbol{w}_k\}\) une famille génératrice de \(W\). Alors \(\boldsymbol{v}\in W^\perp\) si et seulement si \(\boldsymbol{v}\perp \boldsymbol{w}_j\) pour tout \(j=1,\dots,k\).
On sait par hypothèse que \(W=\mathrm{Vect}\{\boldsymbol{w}_1,\dots,\boldsymbol{w}_k\}\).
Si \(\boldsymbol{v}\) est orthogonal à tous les vecteurs de \(W\), il est en
particulier orthogonal à chacun des éléments de la famille génératrice \(\mathcal{B}\).
Inversement, supposons que \(\boldsymbol{v}\) est orthogonal à chacun des éléments de
la base. Comme un élément quelconque \(\boldsymbol{w}\in W\) peut se décomposer dans la
base, \(\boldsymbol{w}=\alpha_1\boldsymbol{w}_1+\cdots+\alpha_k\boldsymbol{w}_k\), la linéarité du
produit scalaire implique que
\[\begin{aligned}
\boldsymbol{v}\cdotp \boldsymbol{w}
&=\boldsymbol{v}\cdotp(\alpha_1\boldsymbol{w}_1+\cdots+\alpha_k\boldsymbol{w}_k)\\
&=
\alpha_1
(\underbrace{\boldsymbol{v}\cdotp\boldsymbol{w}_1}_{=0})
+\cdots+
\alpha_k
(\underbrace{\boldsymbol{v}\cdotp\boldsymbol{w}_k}_{=0})\\
&=0\,,
\end{aligned}\]
et donc \(\boldsymbol{v}\in W^\perp\).
Calcul du complément orthogonal \(W^{\perp\) d'un sous-espace vectoriel \(W \subseteq \mathbb{R}^n\)}
Étant donné un sous-espace vectoriel \(W\) de \(\mathbb{R}^n\), pour calculer \(W^{\perp}\):
Remarque: La preuve de l'identité \(W^{\perp} = \mathrm{Ker}([\boldsymbol{w}_1 \hskip 1mm \cdots \hskip 1mm \boldsymbol{w}_k]^T)\) précédente suit de lemme ci-dessus. En effet, \(\boldsymbol{v} \in \mathrm{Ker}([\boldsymbol{w}_1 \hskip 1mm \cdots \hskip 1mm \boldsymbol{w}_k]^T)\) si et seulement si \[ \boldsymbol{0} = [\boldsymbol{w}_1 \hskip 1mm \cdots \hskip 1mm \boldsymbol{w}_k]^T \boldsymbol{v} = \begin{pmatrix} \boldsymbol{w}_1^T \\ \vdots \\ \boldsymbol{w}_k^T \end{pmatrix} \boldsymbol{v} = \begin{pmatrix} \boldsymbol{w}_1^T \boldsymbol{v} \\ \vdots \\ \boldsymbol{w}_k^T \boldsymbol{v} \end{pmatrix} = \begin{pmatrix} \boldsymbol{w}_1 \cdotp \boldsymbol{v} \\ \vdots \\ \boldsymbol{w}_k \cdotp \boldsymbol{v} \end{pmatrix}\,, \] ce qui équivaut à \(\boldsymbol{w}_1 \cdotp \boldsymbol{v} = \cdots = \boldsymbol{w}_k \cdotp \boldsymbol{v} = 0\). Le lemme précédent nous ainsi que \(\boldsymbol{v} \in \mathrm{Ker}([\boldsymbol{w}_1 \hskip 1mm \cdots \hskip 1mm \boldsymbol{w}_k]^T)\) si et seulement si \(\boldsymbol{v} \in W^{\perp}\).
Exemple: Dans \(\mathbb{R}^3\), considérons les vecteurs \[ \boldsymbol{w}_1= \begin{pmatrix} 1\\ 2\\ 0 \end{pmatrix}\,, \qquad \boldsymbol{w}_2= \begin{pmatrix} -1\\ 3\\ 1 \end{pmatrix}\,, \] et considérons le plan \[ W=\mathrm{Vect}\{\boldsymbol{w}_1,\boldsymbol{w}_2\}\,. \] Le lemme précédent dit que \[ W^\perp=\{\boldsymbol{v}\in\mathbb{R}^3\,:\,\boldsymbol{v}\perp\boldsymbol{w}_1 \text{ et } \boldsymbol{v}\perp \boldsymbol{w}_2\}\,. \] Donc on cherche les vecteurs \(\boldsymbol{v}\in\mathbb{R}^3\) tels que les deux conditions suivantes soient satisfaites simultanément: \[ \begin{cases} \boldsymbol{v}\cdotp \boldsymbol{w}_1=0\,,\\ \boldsymbol{v}\cdotp \boldsymbol{w}_2=0\,. \end{cases} \] Si \(\boldsymbol{v}= \begin{pmatrix} v_1\\ v_2\\ v_3 \end{pmatrix} \), ceci est équivalent à \[ \left\{ \begin{array}{ccccccc} v_1 &+& 2v_2 && &=& 0\,,\\ -v_1 &+& 3v_2 &+& v_3 &=&0\,. \end{array} \right. \] On peut prendre \(v_1\) comme variable libre, et donc on voit que \(W^\perp\) est une droite: \[ W^\perp =\left\{ \boldsymbol{v}= \begin{pmatrix} x_1\\ -x_1/2\\ 5x_1/2 \end{pmatrix} \,\Big|\, x_1\in\mathbb{R} \right\} =\mathrm{Vect}\left\{ \begin{pmatrix} 2\\ -1\\ 5 \end{pmatrix} \right\}\,. \] On vérifie bien dans ce cas que \[\dim(W)+\dim(W^\perp)=2+1=3\,.\]
Exemple: Dans \(\mathbb{R}^4\), considérons les vecteurs \[ \boldsymbol{w}_1= \begin{pmatrix} 1\\ 2\\ -1\\ 0 \end{pmatrix}\,, \qquad \boldsymbol{w}_2= \begin{pmatrix} -1\\ 0\\ 1\\2 \end{pmatrix}\,, \] et considérons le plan \[ W=\mathrm{Vect}\{\boldsymbol{w}_1,\boldsymbol{w}_2\}\,. \] Puisque \(\dim(W)=2\) et que \[\dim(W)+\dim(W^\perp)=4\,,\] on sait que \(\dim(W^\perp)=2\), et donc \(W^\perp\) doit aussi être un plan. Et effectivement, un calcul semblable à celui de l'exemple précédent (voir exercices) montre que \[ W^\perp=\mathrm{Vect}\{\boldsymbol{p}_1,\boldsymbol{p}_2\}\,. \] où \[ \boldsymbol{p}_1= \begin{pmatrix} 1\\ 0\\ 1\\ 0 \end{pmatrix}\,, \qquad \boldsymbol{p}_2= \begin{pmatrix} 2\\ -1\\ 0\\1 \end{pmatrix}\,. \]
Dernière compilation: 2025-09-02 (09:33:30)
Sauf indication contraire, le contenu de ce document est soumis à une licence Creative Commons internationale, Attribution: Pas d'Utilisation Commerciale - Partage dans les Mêmes Conditions 4.0 (CC BY-NC-SA 4.0)
