La méthode des moindres carrés
(également appelée régression linéaire,
linear regression, ou
least squares en anglais) est une technique
qui permet de modéliser des données
expérimentales à l'aide d'un modèle linéaire optimal
(dans un sens que nous préciserons).
Elle est utilisée dans beaucoup de domaines, et
constitue en particulier un des piliers des méthodes de base
rencontrées en machine learning.
De notre point de vue, la méthode des moindres carrés sera une
application de l'algèbre linéaire à des
problèmes d'optimisation.
Avant de la décrire en toute généralité, nous allons la motiver sur un exemple
simple, de petite dimension, qui nous permettra de comprendre l'idée de base,
qui sera ensuite généralisée.
Supposons que l'on souhaite étudier la relation permettant de
convertir les unités de mesure d'une température,
de Celcius (notée \(T_C\))
en Fahrenheit (notée \(T_F\)).
On se souvient que cette relation est du type suivant:
\[(t):\qquad T_F=\alpha T_C+\beta\,, \]
mais on ne se souvient plus des valeurs de \(\alpha\) et \(\beta\).
Si on dispose de deux thermomètre, un qui mesure en Celcius, l'autre en
Fahrenheit, on peut prendre des mesures et les utiliser pour essayer de
retrouver les valeurs des coefficients \(\alpha\) et \(\beta\).
Si ces
thermomètres permettaient de faire des mesures ''parfaites'', il suffirait de
faire deux mesures de températures assez différentes,
\((T_C^{(1)},T_F^{(1)})\) (au milieu du laboratoire par exemple)
et
\((T_C^{(2)},T_F^{(2)})\) (dans le frigo par exemple), de les injecter dans
\((t)\),
\[\begin{aligned}
\alpha T_C^{(1)}+\beta&=T_F^{(1)}\\
\alpha T_C^{(2)}+\beta&=T_F^{(2)}\,,
\end{aligned}\]
et de résoudre ce système pour trouver \(\alpha\) et \(\beta\).
Mais on sait que des mesures empiriques ne sont par définition pas parfaites:
un processus de mesure de ce genre peut contenir de multiples sources d'erreur:
mauvaise calibration des
appareils, minivariations de températures entre les points où la température est
mesurée, imprécisions lors de la lecture de la température sur les thermomètres,
etc.
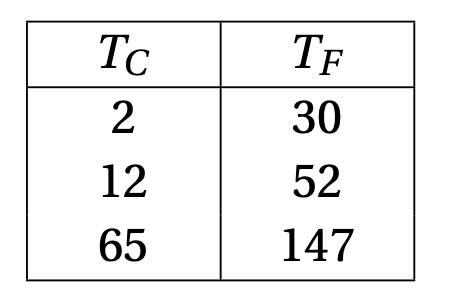
Supposons pour simplifier que l'on fasse trois
mesures. On les reporte dans un tableau:
Encore une fois, comme nos mesures ne sont pas exactes, il est très peu
probable que les trois points satisfassent simultanément la relation
\(T_F=\alpha T_C+\beta\), pour des coefficients \(\alpha,\beta\) bien définis.
En d'autres termes, le système
\[
\left\{
\begin{array}{ccccc}
2\alpha &+& \beta &=&30 \\
12\alpha &+& \beta &=&52 \\
65\alpha &+& \beta &=&147
\end{array}
\right.
\]
est incompatible.
Mais on ne doit pas pour autant abandonner la recherche de la vraie
relation qui
lie ces températures! Car si des mesures expérimentales ne permettent pas de
retrouver exactement une relation théorique, elles permettent néanmoins de s'en
approcher.
D'un point de vue graphique, le problème rencontré ci-dessus peut s'exprimer
comme suit: les trois paires \((T_C,T_F)\) mesurées en laboratoire peuvent être
représentées comme des points dans le plan:
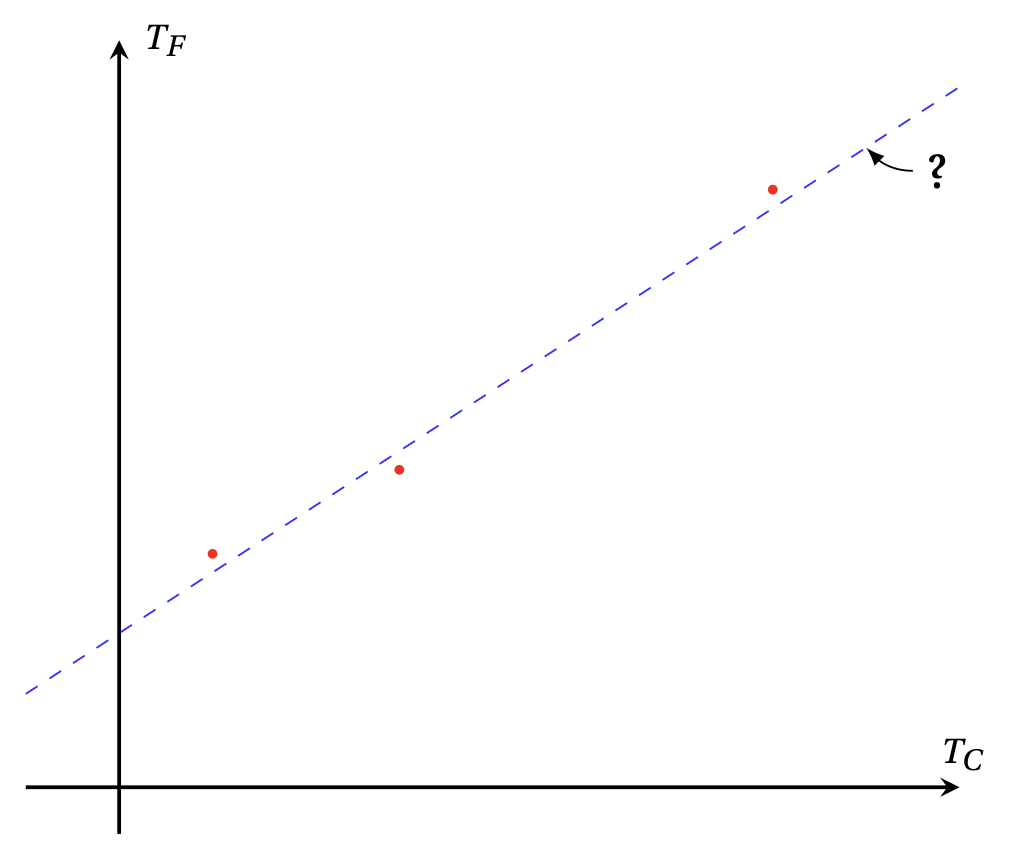
Si ces points ne sont pas sur une même droite,
ils doivent quand-même être proches de la droite
théorique ''\(T_F=\alpha T_C+\beta\)''.
Et on peut donc se poser la question de savoir si il est possible,
à partir de nos trois mesures, de calculer
une paire \((\alpha_*,\beta_*)\) qui donne une droite
\(T_F=\alpha_*T_C+\beta_*\)
qui approxime au mieux ce nuage
de trois points. Comment définir cette droite?
Pour répondre à cette question,
utilisons le langage de l'algèbre linéaire pour formuler précisément le
problème.
On l'a dit, avec nos trois mesures, on est mené au système \(3\times 2\)
\[
\underbrace{\begin{pmatrix}
2&1\\
12&1\\
65&1
\end{pmatrix}}_{=A}
\underbrace{\begin{pmatrix} \alpha\\ \beta \end{pmatrix}}_{=\boldsymbol{x}}
=
\underbrace{\begin{pmatrix} 30\\52 \\147 \end{pmatrix}}_{=\boldsymbol{b}}\,,
\]
qui est incompatible, et qui le sera en général dès que ces trois
mesures sont faites en laboratoire.
Il est utile de formuler géométriquement
l'absence de solution au problème \(A\boldsymbol{x}=\boldsymbol{b}\) ci-dessus, en
reprenant la définition de base du produit matriciel:
\[
\alpha
\underbrace{\begin{pmatrix} 2\\12 \\65 \end{pmatrix}}_{=:\boldsymbol{a}_1}
+\beta
\underbrace{\begin{pmatrix} 1\\1 \\1 \end{pmatrix}}_{=:\boldsymbol{a}_2}
=
\underbrace{\begin{pmatrix} 30\\52 \\147 \end{pmatrix}}_{=:\boldsymbol{b}}
\]
Ce système posséderait une solution \((\alpha,\beta)\) si \(\boldsymbol{b}\)
appartenait à \(\mathrm{Col}(A)\), c'est-à-dire
au plan engendré par \(\boldsymbol{a}_1\) et \(\boldsymbol{a}_2\). Mais le plus
probable est que \(\boldsymbol{b}\) ne soit pas dans ce plan:
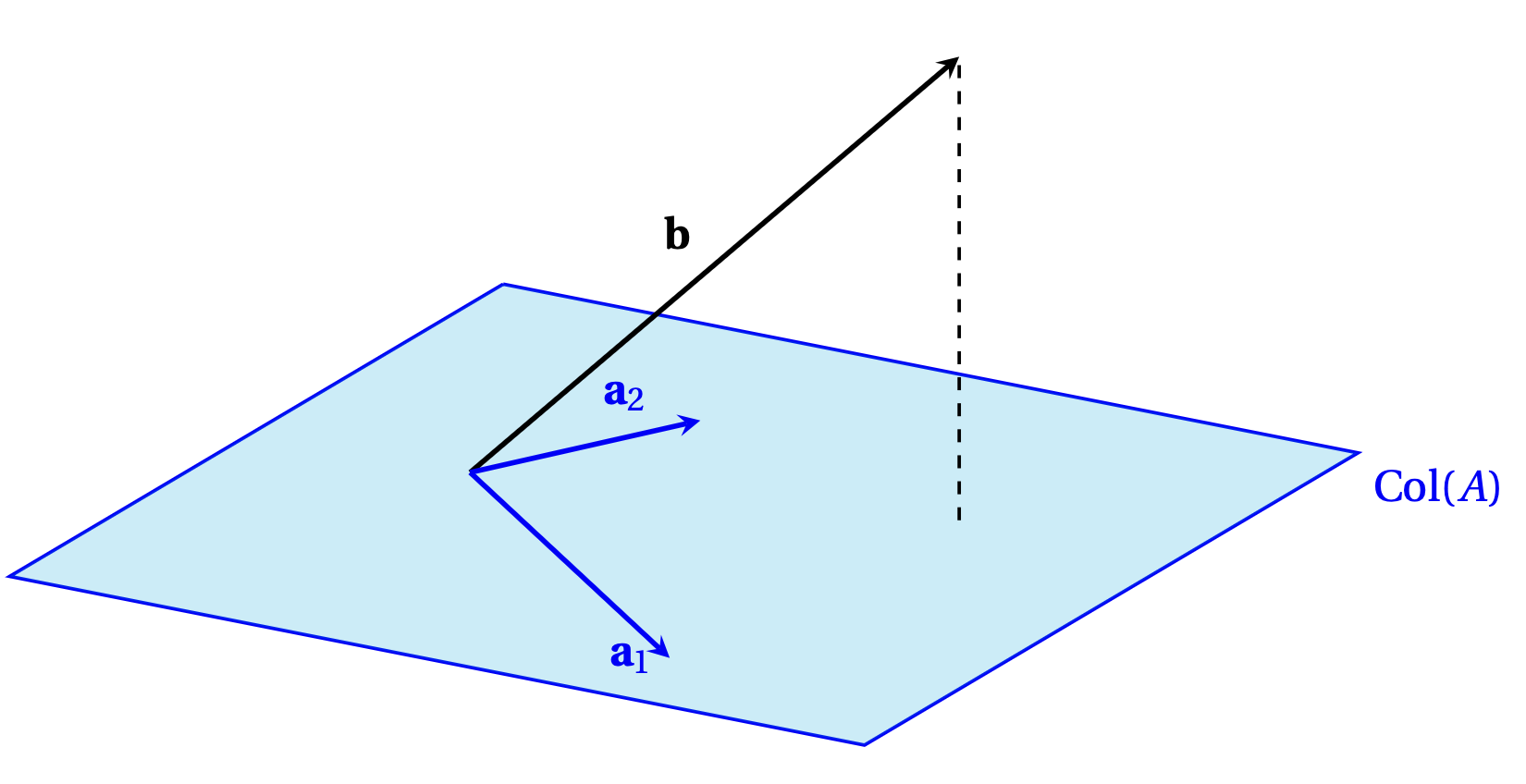
Cette image suggère que malgré tout, si on ne peut pas trouver de paire telle que la combinaison linéaire \(\alpha \boldsymbol{a}_1+\beta\boldsymbol{a}_2\) soit exactement égale à \(\boldsymbol{b}\), on pourrait chercher la paire telle que la combinaison linéaire \(\alpha \boldsymbol{a}_1+\beta\boldsymbol{a}_2\) soit aussi proche que possible de \(\boldsymbol{b}\), c'est à dire la paire \((\alpha,\beta)\) qui minimise la distance \[ \|(\alpha\boldsymbol{a}_1+\beta\boldsymbol{a}_2)-\boldsymbol{b}\|\,. \] On sait, par les résultats démontrés dans le chapitre précédent, que la combinaison linéaire qui réalise ce minimum est précisément celle qui est égale à la projection de \(\boldsymbol{b}\) sur l'espace engendré par \(\boldsymbol{a}_1\) et \(\boldsymbol{a}_2\), à savoir \(\mathrm{Col}(A)\):
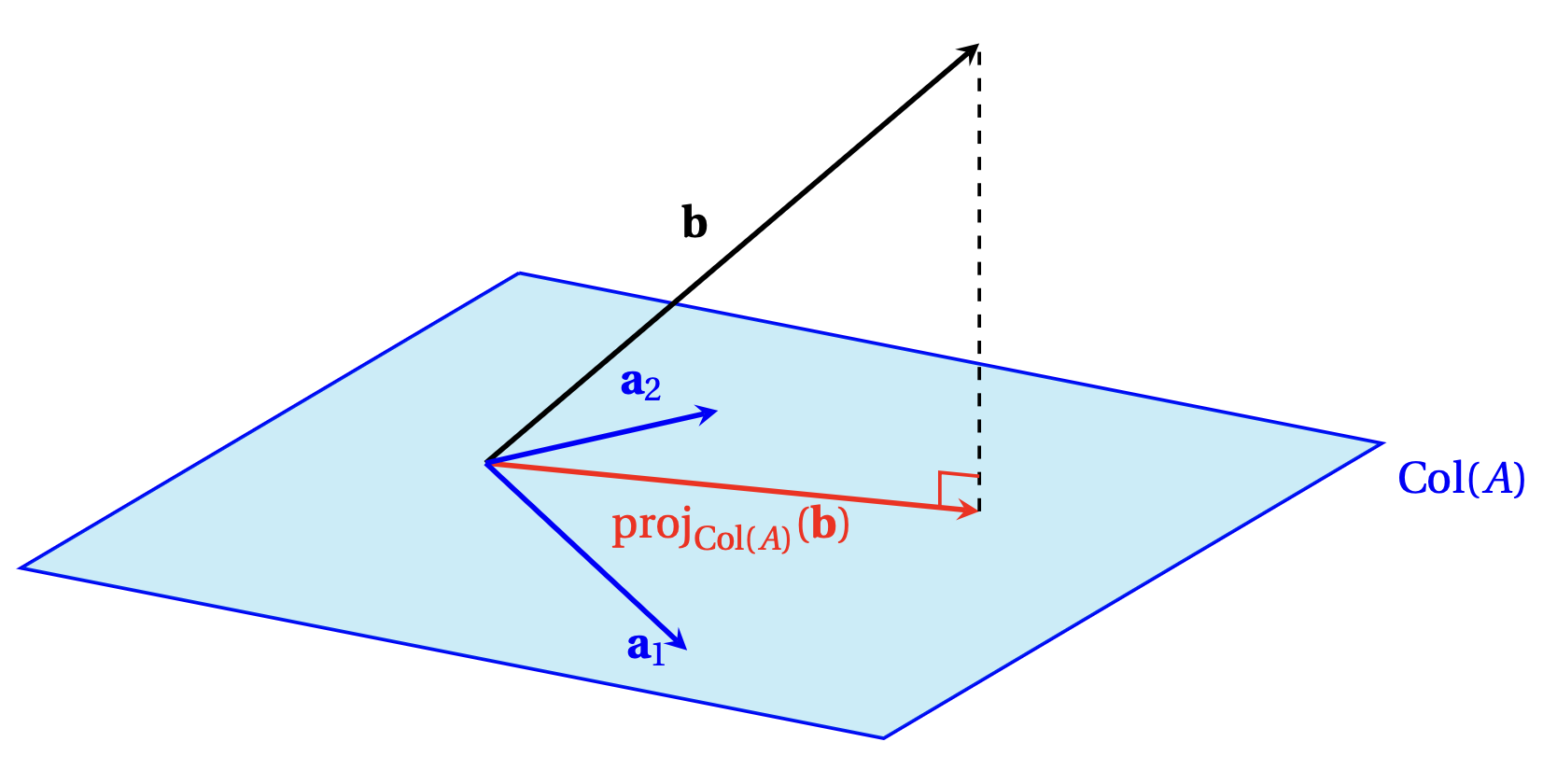
Pour résumer, au lieu de résoudre le système incompatible
\[
(*):\qquad A\boldsymbol{x}=\boldsymbol{b}\,,
\]
on cherche le \(\boldsymbol{x}\) qui minimise la distance
\[ \|A\boldsymbol{x}-\boldsymbol{b}\|\,,
\]
et on sait que ce \(\boldsymbol{x}\) correspond à la solution de
\[
(*)_{MC}:\qquad A\boldsymbol{x}=\mathrm{proj}_{\mathrm{Col}(A)}(\boldsymbol{b})\,.
\]
Ce deuxième système possède toujours une solution \(\boldsymbol{x}\),
puisque par
définition, la projection \(\mathrm{proj}_{\mathrm{Col}(A)}(\boldsymbol{b})\in \mathrm{Col}(A)\).
Calculons donc la projection de \(\boldsymbol{b}\) sur
\(W=\mathrm{Col}(A)=\mathrm{Vect}\{\boldsymbol{a}_1,\boldsymbol{a}_2\}\).
Comme les
colonnes de \(A\) ne sont pas orthogonales, on peut d'abord faire
(Gram-Schmidt):
\[
\boldsymbol{a}_2':= \boldsymbol{a}_2-\mathrm{proj}_{\boldsymbol{a}_1}(\boldsymbol{a}_2)
=
\begin{pmatrix} 1\\1 \\1 \end{pmatrix}
-\frac{79}{4373}
\begin{pmatrix} 2\\12 \\65 \end{pmatrix}
=
\begin{pmatrix} 4215/4373\\ 3425/4373 \\ -762/4373\end{pmatrix}\,.
\]
La projection peut maintenant se calculer:
\[\begin{aligned}
\mathrm{proj}_{\mathrm{Col}(A)}(\boldsymbol{b})
&=
\frac{\boldsymbol{b}\cdotp \boldsymbol{a}_1}{\|\boldsymbol{a}_1\|^2}\boldsymbol{a}_1
+
\frac{\boldsymbol{b}\cdotp \boldsymbol{a}_2'}{\|\boldsymbol{a}_2'\|^2}\boldsymbol{a}_2'\\
&=
\frac{10239}{4373}
\begin{pmatrix} 2\\12 \\65 \end{pmatrix}
+
\frac{192536}{30077494}
\begin{pmatrix} 4215\\ 3425 \\ -762\end{pmatrix}\\
&=
\begin{pmatrix}
31.6644\dots\\
50.0215\dots\\
147.3140\dots
\end{pmatrix}
\end{aligned}\]
Maintenant, on peut résoudre le système
\(A\boldsymbol{x}=\mathrm{proj}_{\mathrm{Col}(A)}(\boldsymbol{b})\):
\[
\begin{pmatrix}
2&1\\
12&1\\
65&1
\end{pmatrix}
\begin{pmatrix} \alpha\\ \beta \end{pmatrix}
=
\begin{pmatrix}
31.6644\dots\\
50.0215\dots\\
147.3140\dots
\end{pmatrix}
\]
On trouve:
\[\begin{aligned}
\alpha&=1.8357\dots\\
\beta&=27.9930\dots
\end{aligned}\]
Donc nos trois mesures, et le raisonnement géométrique menant à projeter sur les
colonnes de la matrice \(A\), nous ont mené à la version suivante de la relation
entre degrés Celsius et Fahrenheit:
\[T_F=1.8357\dots T_C+27.9930\dots\,, \]
Cette droite est celle qui approxime le mieux nos mesures,
au sens des moindre carrés (voir la section suivante pour l'explication
de cette terminologie).
Pour information, la vraie relation, que l'on trouve par exemple
ici, est la suivante:
\[T_F=\frac{9}{5}T_C+32=1.8T_C+32\,.\]
Avec seulement trois points, notre méthode fournit donc des coefficients dont
l'erreur avec la relation théorique est d'environ
\(2\%\) pour \(\alpha\), et \(13\%\) pour \(\beta\).
Dernière compilation: 2023-08-30 (14:16:46)
Sauf indication contraire, le contenu de ce document est soumis à une licence Creative Commons internationale, Attribution: Pas d'Utilisation Commerciale - Partage dans les Mêmes Conditions 4.0 (CC BY-NC-SA 4.0)
